【OpenCV-Python】教程：7-7 PCA

OpenCV Python PCA

【目标】

• 利用 pca 来计算目标的方向

【理论】

Introduction to Principal Component Analysis (PCA)

PCA（主成分分析）是提取最重要特征的统计过程。

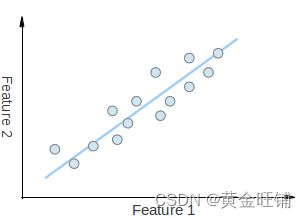
假设你有一组2D点，如上图所示。每个维度都对应于您感兴趣的特性。有些人可能会说，这些点是按随机顺序设置的。然而，如果你仔细观察，你会发现有一个很难忽视的线性模式(由蓝线表示)。主成分分析的关键是降维。降维是减少给定数据集的维数的过程。例如，在上述情况下，可以将点集近似为一条线，因此，将给定点的维数从2D降至1D。

此外，您还可以看到，这些点沿蓝线变化最大，超过它们沿特征1或特征2轴的变化。这意味着，如果你知道一个点沿蓝线的位置，你就比只知道它在特征1轴或特征2轴上的位置有更多关于这个点的信息。

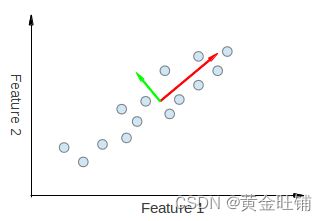
因此，PCA允许我们找到数据变化最大的方向。事实上，在图中的点集上运行主成分分析的结果由两个被称为特征向量的向量组成，它们是数据集的主成分。

每个特征向量的大小被编码在相应的特征值中，并表示数据沿主成分的变化程度。特征向量的起点是数据集中所有点的中心。将PCA应用于N维数据集，得到N个N维特征向量、N个特征值和1个N维中心点。

特征向量和特征值的计算

目标是将一个给定的维度 p的数据集 X转换为一个维度更小的 l的备选数据集 Y，等价地，我们正在寻找矩阵 Y，其中 Y是矩阵 X的 Karhunen-Loève变换(KLT):

$$Y=\mathbb{KLT}\{X\}$$

组织数据

假设你有一组包含 p个变量的观察数据，你想要缩减数据，以便每个观察结果都可以用 L 个变量来描述，L < p。进一步假设，一组 n 个数据向量 $x_1\dots x_n$， 其中每个 $x_i$ 表示的就是一个单独的 p 个变量的一个数据。

• 将 $x_1...x_n$ 为行向量，每个有 $p$ 列
• 将所有行向量放到矩阵$X$里，构建一个矩阵 $X$, 维度为 $n\times p$

计算经验平均值

• 沿着维度 $j=1,...,p$，计算经验均值
• 将计算出的平均值放入维度为$p\times 1$的经验平均向量$u$中。

$$u[j]=\frac{1}{n}\sum _{i=1}^{n}X[i,j]$$

计算均值的偏差

均值减法是寻找主成分基的解决方案的一个组成部分，使接近数据的均方误差最小化。因此，我们将数据居中，如下所示:

• 从数据矩阵$X$的每一行中减去经验平均向量$u$。
• 将偏差数据存入矩阵 $B$ 中，

$$B=X-h{u}^T$$

其中 $h$为 全 1 的 $n\times 1$ 向量，即

$$h[i]=1,i=1,...,n$$

求协方差矩阵

• 找到 $p\times p$ 经验协方差矩阵 $C$

$$C=\frac{1}{n-1}{B}^{\ast }\cdot B$$

其中$\ast$是共轭转置算子。请注意，如果B完全由实数组成，这是在许多应用中的情况，“共轭转置”与常规转置相同。

找出协方差矩阵的特征向量和特征值

• 计算特征向量的矩阵V，它对角化协方差矩阵C:

$$V^{-1}CV=D$$

其中 $D$ 是 $C$ 特征值的对角化矩阵。

• 矩阵$D$将采用$p\times p$对角矩阵的形式:

$$D[k,l]=\{\begin{array}{ll}{\lambda }_k,& k=l\\ 0,& k\ne l\end{array}$$

其中，${\lambda }_j$ 是 协方差矩阵 $C$ 的 $j$ 个特征值

• 矩阵$V$，同样是$p\times p$的，包含$p$个列向量，每个列向量的长度都是$p$，它们表示协方差矩阵$C$的$p$个特征向量。
• 特征值和特征向量是有序配对的。第$j$个特征值对应于第$j$个特征向量。

【代码】

import cv2
import numpy as np
import argparse
from math import atan2, cos, sin, sqrt, pi


def drawAxis(img, p_, q_, colour, scale):
    p = list(p_)
    q = list(q_)

    angle = atan2(p[1] - q[1], p[0] - q[0])  # angle in radians
    hypotenuse = sqrt((p[1] - q[1]) * (p[1] - q[1]) +
                      (p[0] - q[0]) * (p[0] - q[0]))
  
    # 
    q[0] = p[0] - scale * hypotenuse * cos(angle)
    q[1] = p[1] - scale * hypotenuse * sin(angle)
    cv2.line(img, (int(p[0]), int(p[1])),
            (int(q[0]), int(q[1])), colour, 1, cv2.LINE_AA)
  
    # 创建箭头钩
    p[0] = q[0] + 9 * cos(angle + pi / 4)
    p[1] = q[1] + 9 * sin(angle + pi / 4)
    cv2.line(img, (int(p[0]), int(p[1])),
            (int(q[0]), int(q[1])), colour, 1, cv2.LINE_AA)
    p[0] = q[0] + 9 * cos(angle - pi / 4)
    p[1] = q[1] + 9 * sin(angle - pi / 4)
    cv2.line(img, (int(p[0]), int(p[1])),
            (int(q[0]), int(q[1])), colour, 1, cv2.LINE_AA)


def getOrientation(pts, img):
    sz = len(pts)
    data_pts = np.empty((sz, 2), dtype=np.float64)
    for i in range(data_pts.shape[0]):
        data_pts[i, 0] = pts[i, 0, 0]
        data_pts[i, 1] = pts[i, 0, 1]
  
    # 执行 PCA 分析
    mean = np.empty((0))
    mean, eigenvectors, eigenvalues = cv2.PCACompute2(data_pts, mean)
  
    # 存储物体的中心
    cntr = (int(mean[0, 0]), int(mean[0, 1]))

    cv2.circle(img, cntr, 3, (255, 0, 255), 2)
    p1 = (cntr[0] + 0.02 * eigenvectors[0, 0] * eigenvalues[0, 0],
          cntr[1] + 0.02 * eigenvectors[0, 1] * eigenvalues[0, 0])
    p2 = (cntr[0] - 0.02 * eigenvectors[1, 0] * eigenvalues[1, 0],
          cntr[1] - 0.02 * eigenvectors[1, 1] * eigenvalues[1, 0])
    drawAxis(img, cntr, p1, (0, 255, 0), 1)
    drawAxis(img, cntr, p2, (255, 255, 0), 5)
    # orientation in radians
    angle = atan2(eigenvectors[0, 1], eigenvectors[0, 0])

    return angle


imname = "assets/pca_test2.jpg"
src = cv2.imread(imname)
# Check if image is loaded successfully
if src is None:
    print('Could not open or find the image: ', imname)
    exit(0)
# cv2.imshow('src', src)

# 图像预处理和找轮廓
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
_, bw = cv2.threshold(gray, 50, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)
contours, _ = cv2.findContours(bw, cv2.RETR_LIST, cv2.CHAIN_APPROX_NONE)

for i, c in enumerate(contours):
    # 计算每个轮廓的面积
    area = cv2.contourArea(c)
  
    # 忽略太小和太大的轮廓
    if area < 1e2 or 1e5 < area:
        continue
  
    # 画每一个轮廓
    cv2.drawContours(src, contours, i, (0, 0, 255), 2)
  
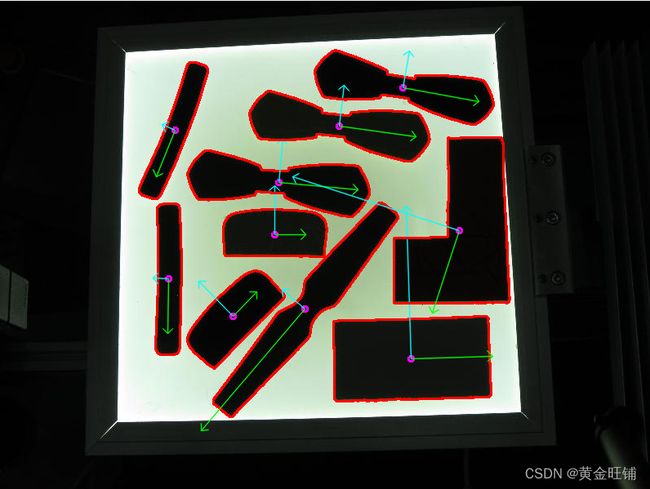
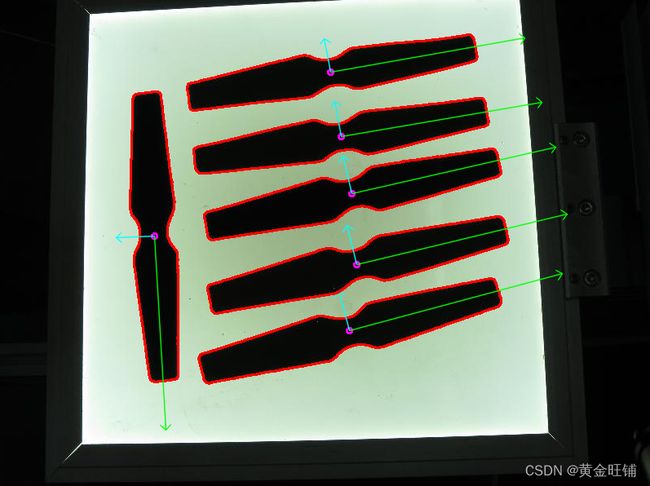
    # 找到每一个形状的方向
    getOrientation(c, src)

cv2.imshow('output', src)
cv2.waitKey()
cv2.destroyAllWindows()

【接口】

• PCACompute

cv2.PCACompute(	data, mean[, eigenvectors[, maxComponents]]	) ->	mean, eigenvectors
cv2.PCACompute(	data, mean, retainedVariance[, eigenvectors]	) ->	mean, eigenvectors
cv2.PCACompute2(	data, mean[, eigenvectors[, eigenvalues[, maxComponents]]]	) ->	mean, eigenvectors, eigenvalues
cv2.PCACompute2(	data, mean, retainedVariance[, eigenvectors[, eigenvalues]]	) ->	mean, eigenvectors, eigenvalues

wrap PCA::operator() , performs PCA

• data: 输入的数据
• mean: 均值，
• eigenvectors: 特征向量
• eigenvalues: 特征值
• maxComponents: 最多主成分数量, 默认就是所有的主成分
• retainedVariance: 主成分分析应保留的方差百分比。使用此参数将让PCA决定保留多少个组件，但它总是至少保留2个

【参考】

1. Introduction to Principal Component Analysis (PCA)
2. https://robospace.wordpress.com/2013/10/09/object-orientation-principal-component-analysis-opencv/
3. sources [1], [2] and special thanks to Svetlin Penkov for the original tutorial.
4. cv::PCA Class Reference
5. OpenCV: Operations on arrays