MATLAB绘制椭圆

一、根据椭圆方程：axx+bxy+cyy+dx+ey = f画椭圆

【例1】已知椭圆方程：xx + 2xy + 3yy + 4x + 5*y = 6
第一种方法： 调用MATLAB自带的ezplot函数画椭圆

ezplot('x^2+2*x*y+3*y^2+4*x+5*y = 6')
axis([-6 3 -3 3]);

图形如下所示：

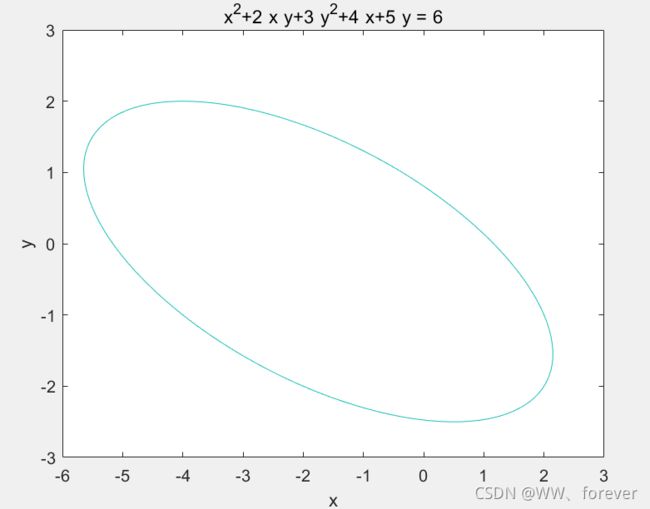
第二种方法： 调用自编的ellipsefig1函数画椭圆。
ellipsefig1函数的代码如下：

function  h = ellipsefig1(a,b,c,d,e,f)
% 画一般椭圆：ax*x+bx*y+c*y*y+d*x+e*y = f
delta = b^2-4*a*c;
if delta >= 0
    warning('这不是一个椭圆')
    return;
end
x0 = (b*e-2*c*d)/delta;
y0 = (b*d-2*a*e)/delta;
r = a*x0^2 + b*x0*y0 +c*y0^2 + f;
if r <= 0
    warning('这不是一个椭圆')
    return;
end

aa = sqrt(r/a);
bb = sqrt(-4*a*r/delta);
t = linspace(0, 2*pi, 60);
xy = [1 -b/(2*a);0 1]*[aa*cos(t);bb*sin(t)];
h = plot(xy(1,:)-x0,xy(2,:)-y0, 'k', 'linewidth', 2);

ellipsefig1函数的原理是通过配方将一般椭圆方程化为标准椭圆方程，作出标准椭圆曲线，然后通过坐标旋转和缩放得到所要的椭圆曲线图像。

ellipsefig1(1,2,3,4,5,6);

第三种方法： 调用自编的ellipsefig2函数画椭圆。ellipsefig2函数的代码如下：

function  h = ellipsefig2(a,b,c,d,e,f)
% 画一般椭圆：ax*x+bx*y+c*y*y+d*x+e*y = f
P = [a b/2;b/2 c];
delta = b^2-4*a*c;
if delta >= 0
    warning('这不是一个椭圆')
    return;
end
x0 = (b*e-2*c*d)/delta;
y0 = (b*d-2*a*e)/delta;
r = a*x0^2 + b*x0*y0 +c*y0^2 + f;
if r <= 0
    warning('这不是一个椭圆')
    return;
end

[V, D] = eig(P);
aa = sqrt(r/D(1));
bb = sqrt(r/D(4));
t = linspace(0, 2*pi, 60);
xy = V*[aa*cos(t);bb*sin(t)];
h = plot(xy(1,:)-x0,xy(2,:)-y0, 'k', 'linewidth', 2);

ellipsefig2函数的原理是利用线性代数中所讲的二次型化标准型的办法将一般椭圆方程化为标准椭圆方程，先作出标准椭圆曲线，然后通过坐标旋转得到所要的椭圆曲线图像。

ellipsefig2(1,2,3,4,5,6);

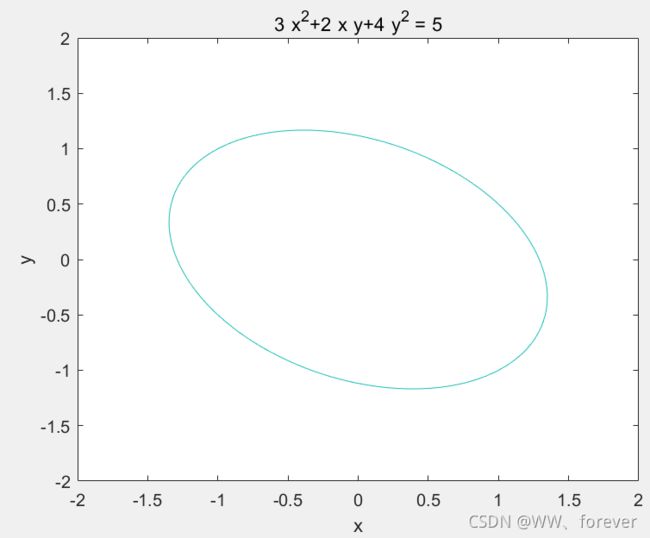
【例2】已知椭圆方程：[x,y][3, 1;1, 4][x,y]’ = 5，即3xx + 2xy + 4yy = 5
可用MATLAB自带的ezplot函数，或自编的ellipsefig1和ellipsefig2函数画此椭圆，命令分别如下：

ezplot('3*x^2+2*x*y+4*y^2 = 5')
axis([-2 2 -2 2])

ellipsefig1(3,2,4,0,0,5);

ellipsefig2(3,2,4,0,0,5);

图形如下所示：

二、根据椭圆中心坐标、长半轴、偏心率和方向角画椭圆

【例3】已知椭圆中心坐标为[1, 2]，长半轴为10，短半轴为5，方向角为45°。
调用MATLAB自带的ellipse1函数画此椭圆，ellipse1函数根据椭圆中心坐标、长半轴、偏心率和方向角画椭圆。

ecc = axes2ecc(10,5);  % 根据长半轴和短半轴计算椭圆偏心率
[elat,elon] = ellipse1(1,2,[10 ecc],45);
plot(elat,elon)

图形如下所示：

【ellipse1函数】
语法：
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid,angleUnit,npts)

参考

Matlab如何画椭圆（总结帖）