【PyTorch】深度学习实践之 CNN基础篇——卷积神经网络跑Minst数据集
本文目录
- 1. 全连接神经网络与卷积神经网络
- 2. 图像的本质
- 3. 卷积运算
- 3.1 单通道卷积运算
- 3.2 三通道卷积运算
- 3.3 卷积层其他的权重
- 4. 池化运算(下采样)
- 5. 实现简单的卷积神经网络
- 实现代码:
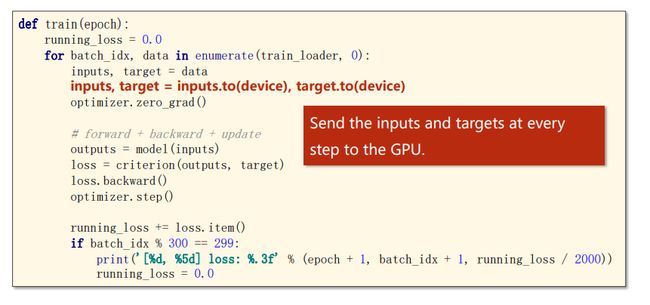
- 使用gpu跑模型
- 结果:
- 课后练习:实现更复杂的CNN
- 实现代码:
- 结果:
- 学习资料
- 系列文章索引
1. 全连接神经网络与卷积神经网络
之前学习的网络为全连接神经网络,一层一层的全部连接,也就是前一层的每一个节点都会和后面一层的所有节点进行连接。全连接网络在数值计算的时候,会把信息拉成一维的,这样会丧失掉图片特征中的一些空间的信息。
卷积神经网络可以很好的保留图像的空间特征,其基本工作方式如下:
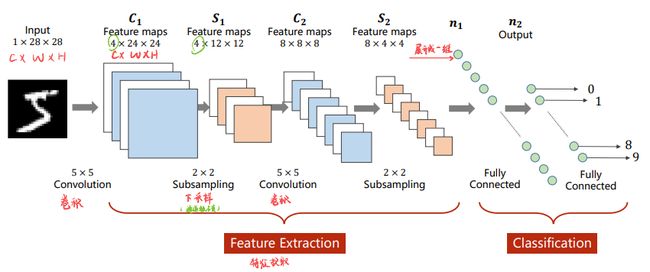
- 输入一张图像,先进行卷积操作,然后通过下采样减少元素数量,降低运算的需求 … 最终为了实现分类,输出还是一个10维的向量。中间的过程可以采样不同的方式。
总的来看,首先经过卷积层,进行特征提取,经过特征提取之后,图片信息变成了一个向量;而后将向量接入一个全连接网络进行分类处理。
卷积和下采样称为特征提取器,全连接层作为分类器。
2. 图像的本质
图像一般是栅格图像,每一个格子代表一个像素,图像信息一般有W(宽)H(高)C(通道)。一般通道分为RGB,如图右侧所示。
3. 卷积运算
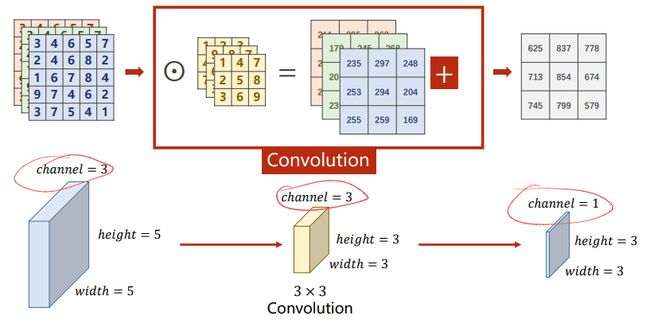
3.1 单通道卷积运算
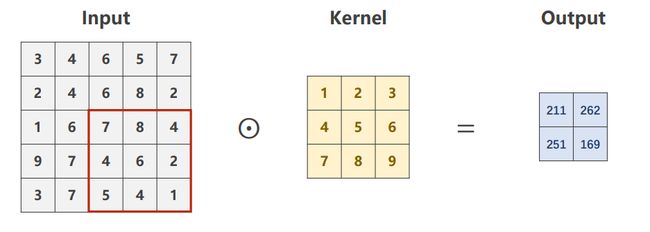
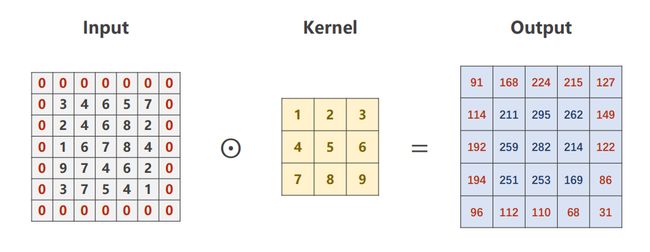
如图所示,选择 1 x 5 x 5 的单通道图像,3 x 3 的卷积核,进行卷积运算:
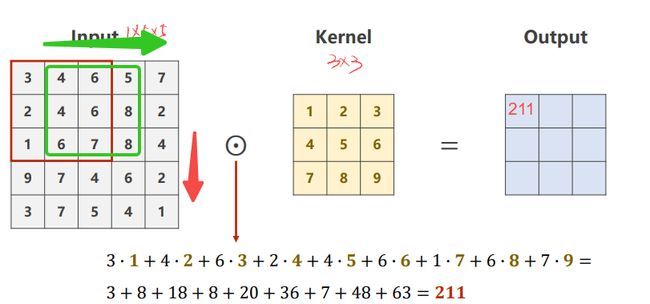
步骤:先在输入图像中,画出一个卷积核大小的(3x3)的窗口,而后将该窗口与卷积核做数乘+求(对应元素相乘);然后将该窗口从左往右、从上到下做遍历(华东),每一次都进行数乘求和运算,最终由这些数乘求和数值组成的矩阵,就是卷积后的结果。
3.2 三通道卷积运算
对于输入图像,每一个通道都会配一个卷积核**(输入图像的通道数 == 卷积核的通道数)**
每个通道根据上面讲的单通道的计算方式计算,得到一个矩阵,一共可以得到三个矩阵,将这三个矩阵求和,最终得到的结果就是三通道卷积的结果。

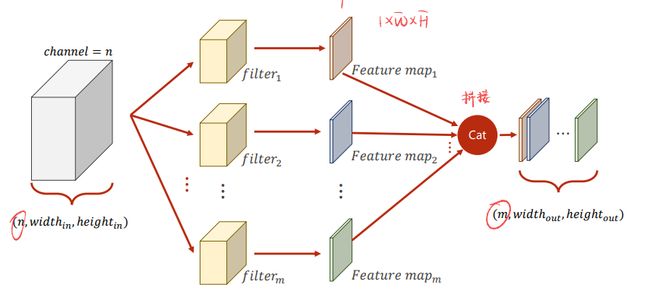
可以看到,只有一个卷积核,最终输出的是一个通道的结果。怎么输出多个通道呢?
在pytorch里面,卷积核kernel_size = 常数,代表是一个常数x常数的卷积核,而kernel_size也可以设置为一个元组,比如kernel_size=(5,3)代表卷积核的大小为长方形5x3,但是我们经常使用的卷积核还是kernel_size=3,代表3x3这样的卷积核。
定义一个卷积层:输入通道、输出通道、卷积核大小。如下图:

3.3 卷积层其他的权重
填充padding:例如我们输入一个5x5大小的输入图像,通过3x3的卷积核进行卷积,此时输出图像为3x3。但是此时我们想要输出图像的大小和输入图像的大小是一样大,此时我们就需要进行对输入图像进行填充,padding = 3/2 = 1,此时就需要在输入图像填充一圈使其变成7x7。
假如我们使用5x5大小的卷积核进行卷积,然后要求输出图像大小等于输入图像大小,此时我们需要填充padding = 5/2 = 2,填充2圈,使得原图像变成9x9。
B:batch_size
C: 通道数
W:图像或卷积核的宽度
H:图像或卷积核的高度
O: 输出通道数
I:输入通道数
stride:步长,就是卷积核窗口在遍历图像时,每走一步的步长。
v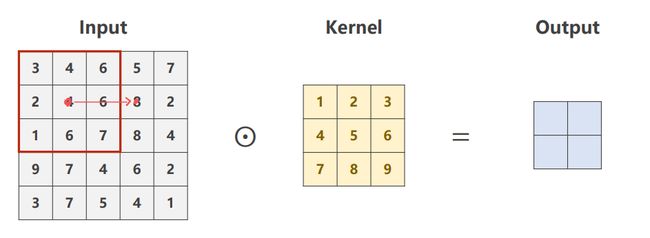
从左到右、从上到下都是每次移动两步。这个可以有效地降低特征图的宽度和高度。

4. 池化运算(下采样)
池化运算常用的是最大池化,它是没有权重的,2x2的池化默认stride=2。

做最大池化,只是在一个通道内进行,不同的通道不会最大池化。所以说,做最大池化,通道的数量不会发生变化,只是2x2的最大池化,图像的大小会变为原来的一半。

5. 实现简单的卷积神经网络
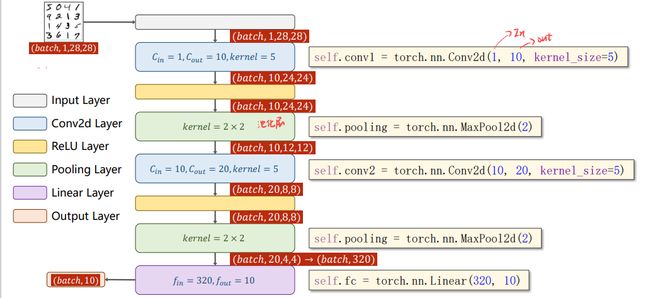
- 选择 5 x 5 的卷积核,输入通道为 1,输出通道为 10:此时图像矩阵经过 5 x 5 的卷积核后会小两圈,也就是4个数位,变成 24 x 24,输出通道为10;
- 选择 2 x 2 的最大池化层:此时图像大小缩短一半,变成 12 x 12,通道数不变;
- 再次经过 5 x 5 的卷积核,输入通道为 10,输出通道为 20:此时图像再小两圈,变成 8 *8,输出通道为20;
- 再次经过 2 x 2 的最大池化层:此时图像大小缩短一半,变成 4 x 4,通道数不变;
- 最后将图像整型变换成向量,输入到全连接层中:输入一共有 4 x 4 x 20 = 320 个元素,输出为 10.
注意:5x5的卷积核就是少两圈,也就是图像大小 -4;3x3卷积核少一圈,图像 -2;2x2池化层图像大小缩小一半。
实现代码:
import torch
import torch.nn as nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as f
import torch.optim as optim
import matplotlib.pyplot as plt
# 准备数据集
batch_size = 64
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.1307,],std=[0.3081,])
])
train_dataset = datasets.MNIST(root="./mnist_data/",train=True,transform=transform,download=False)
test_dataset = datasets.MNIST(root="./mnist_data/",train=False,transform=transform,download=False)
train_dataloader = DataLoader(dataset=train_dataset,batch_size=batch_size,shuffle=True)
test_dataloader = DataLoader(dataset=test_dataset,batch_size=batch_size,shuffle=True)
# 网络模型
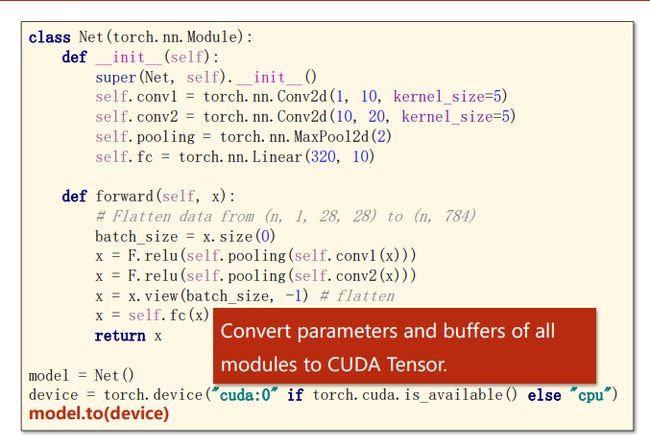
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.conv1 = nn.Conv2d(1,10,kernel_size=5)
self.conv2 = nn.Conv2d(10,20,kernel_size=5)
self.pooling = nn.MaxPool2d(2)
self.fc = nn.Linear(320,10)
def forward(self,x):
# Flatten data from (n,1,28,28) to (n,784)
x = f.relu(self.conv1(x))
# batch_size = x.size(0)
x = self.pooling(x)
x = f.relu(self.conv2(x))
x = self.pooling(x)
x = x.view(x.size()[0],-1)
x = self.fc(x)
return x
# x = f.relu(self.pooling(self.conv1(x)))
# x = f.relu(self.pooling(self.conv2(x)))
# x = x.view(x.size(0), -1)
# x = self.fc(x)
# return x
model = Model()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)
# 优化器和损失函数
criterion = nn.CrossEntropyLoss(reduction='mean')
optimizer = optim.SGD(model.parameters(),lr = 0.01,momentum=0.5)
# 训练
epoch_list = []
def train(epoch):
running_loss = 0.0
epoch_list.append(epoch+1)
# for epoch in range(10):
for i, data in enumerate(train_dataloader, 0):
input, target = data
input, target = input.to(device),target.to(device)
y_pred = model(input)
loss = criterion(y_pred, target)
# print(i+1,epoch+1,loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()
if i % 300 == 299:
print("{} {} loss:{:.3f}".format(epoch + 1, i + 1, running_loss / 300))
running_loss = 0.0
# 测试
accuracy_list = []
def test():
total = 0
correct = 0
with torch.no_grad():
for i,data in enumerate(test_dataloader,0):
input,target = data
input, target = input.to(device), target.to(device)
y_pred = model(input)
predicted = torch.argmax(y_pred.data,dim=1)
total += target.size(0)
correct += (predicted==target).sum().item()
accuracy = correct/total
accuracy_list.append(accuracy)
print("Accuracy on test set:{:.2f} %".format(100*correct/total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
#画图
plt.plot(epoch_list,accuracy_list)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.grid()
plt.show()
使用gpu跑模型
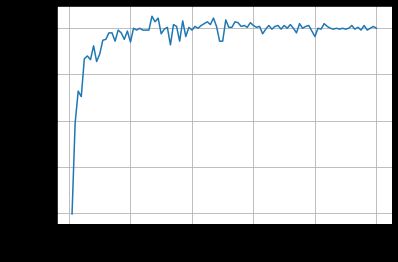
结果:
训练轮数增加可以看到准确率提高。
课后练习:实现更复杂的CNN
实现更复杂的CNN,查看与上述CNN性能区别。
实现代码:
更改了模型
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.conv1 = nn.Conv2d(1,16,kernel_size=3) # (1,28,28) to (16,26,26)
self.conv2 = nn.Conv2d(16,32,kernel_size=3) # (16,13,13) to (32,11,11)
self.conv3 = nn.Conv2d(32,64,kernel_size=3) # (32,5,5) to (64,3,3)
self.pooling = nn.MaxPool2d(2)
self.fc1 = nn.Linear(64,32)
self.fc2 = nn.Linear(32,16)
self.fc3 = nn.Linear(16,10)
def forward(self,x):
x = f.relu(self.conv1(x))
x = self.pooling(x)
x = f.relu(self.conv2(x))
x = self.pooling(x)
x = f.relu(self.conv3(x))
x = self.pooling(x)
x = x.view(x.size()[0],-1)
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
return x
结果:
和原来的CNN网络相比没有太大区别,只是看起来前期的acc曲线上升更快。
学习资料
- https://blog.csdn.net/qq_42585108/article/details/108220096
- https://blog.csdn.net/lizhuangabby/article/details/125730151?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_title~default-0-125730151-blog-108220096.pc_relevant_default&spm=1001.2101.3001.4242.1&utm_relevant_index=3
系列文章索引
教程指路:【《PyTorch深度学习实践》完结合集】 https://www.bilibili.com/video/BV1Y7411d7Ys?share_source=copy_web&vd_source=3d4224b4fa4af57813fe954f52f8fbe7
- 线性模型 Linear Model
- 梯度下降 Gradient Descent
- 反向传播 Back Propagation
- 用PyTorch实现线性回归 Linear Regression with Pytorch
- 逻辑斯蒂回归 Logistic Regression
- 多维度输入 Multiple Dimension Input
- 加载数据集Dataset and Dataloader
- 用Softmax和CrossEntroyLoss解决多分类问题(Minst数据集)
- CNN基础篇——卷积神经网络跑Minst数据集
- CNN高级篇——实现复杂网络
- RNN基础篇——实现RNN
- RNN高级篇—实现分类