Python - Order in chaos 混乱中的秩序之随机点中值连线
一.引言
刷短视频刷到了一个有趣的图形变化,随机给定 N 个点,将 N 个点首尾连接生成一个多边形,随后将每个边的中点连接并得到新的多边形,如此多次循环,最终总会得到一个椭圆形。
A.初始化 N 个点并生成多边形
B.取多边形中点依次连接生成新的多边形
C.持续执行多次
循环多次取中点连线操作 ......
D.最终得到椭圆形
二.Python 实现
1.随机生成N个点并生成多边形
A.获取随机点
# 随机生成(x,y) x,y 为 (0-100) 的整数
def getRandomPoint():
x = int(random.uniform(0, 100))
y = int(random.uniform(0, 100))
return x, yB.生成多边形
# pointNum = N 为指定的 N 个点
for num in range(0, pointNum):
x, y = getRandomPoint()
x_arr.append(x)
y_arr.append(y)
# 这里尾巴添加首个点,达到首尾相连的目的
x_arr.append(x_arr[0])
y_arr.append(y_arr[0])
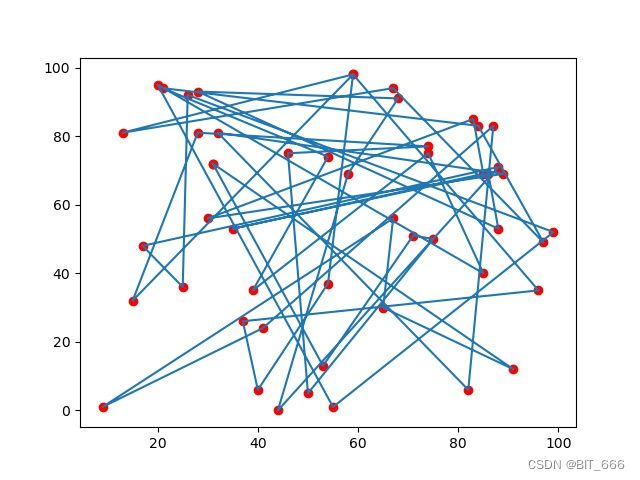
plt.plot(x_arr, y_arr)
plt.show()随机 50 个点,得到第一幅初始图像:
2.多次循环最终得到椭圆
这里循环执行取中点并连接生成多边形的操作,由于 plot 会根据坐标自动调整比例,所以我们看到的图像总是一样大,但是仔细观察坐标系,可以发现原始多边形已经在不断变下,如果这些图放到一个比例下,最终得到的椭圆在我们视角里会接近一个点。
x_arr_new = []
y_arr_new = []
lastIndex = len(x_arr) - 1
for i in range(0, len(x_arr)):
# 防止数组越界
if (i != lastIndex):
x_mid = (x_arr[i] + x_arr[i + 1]) / 2
y_mid = (y_arr[i] + y_arr[i + 1]) / 2
x_arr_new.append(x_mid)
y_arr_new.append(y_mid)
else:
x_mid = (x_arr[i] + x_arr[0]) / 2
y_mid = (y_arr[i] + y_arr[0]) / 2
x_arr_new.append(x_mid)
y_arr_new.append(y_mid)
# 保证收尾连接
x_arr_new.append(x_arr_new[0])
y_arr_new.append(y_arr_new[0])
plt.plot(x_arr_new, y_arr_new)
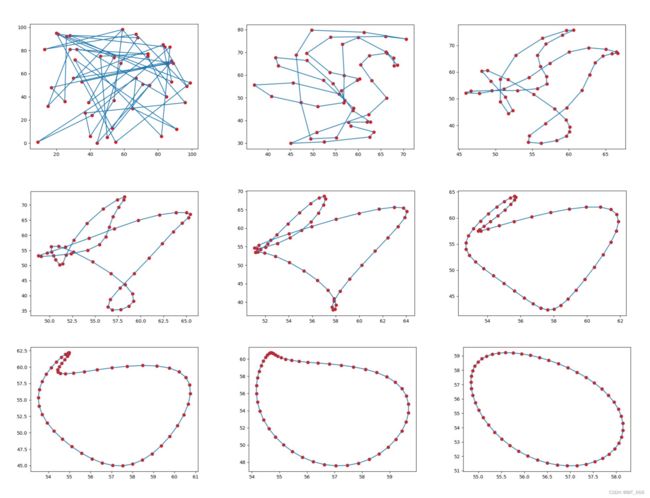
plt.show()上图为原始图形经过2次中点连接后形状的转变,可以看到比例尺也在相应的不断减小,下面用9张图观察图像的变化趋势:
3.将完整流程生成 GIF
为了观察整个流程,我们可以调用 python 库例如 imageio 等将上述生成的图片依次保存并最终生成 gif 图像。
# 生成图形
frames = []
for i in range(0, epoch):
imageName = target_path + str(i) + ".jpg"
frames.append(imageio.imread(imageName))
# 生成 GIF 图形
duration = 10
gifPath = target_path + "all.gif"
imageio.mimsave(gifPath, frames, 'GIF', duration=duration) # 选择'GIF'类型下面展示随机初始化 20 个点并进行 100 次迭代达到的椭圆效果:
4.换个参数试试
原文中取均值中点,下面尝试➗3 取 1/3 节点连接会有什么区别:
换成 1/3 后最终得到的椭圆似乎更圆润一些,不过这里只做了有限次随机试验,不能下太肯定的结论,有兴趣的同学也可以自己修改代码中的方法,看看不同情况下的图像情况。
三.混乱中的秩序
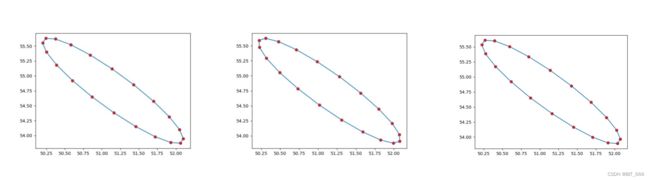
随着迭代次数的增多,最终的椭圆基本不会发生太大的变化:
下面尝试简单发现下其中蕴含什么奥秘,假设有 N 个点 {(x1,y1), (x2,y2), ..., (xn,yn)},经过 N 次迭代后,每一个元素的值为 [Tips: 这里仅计算横坐标、纵坐标同理]:
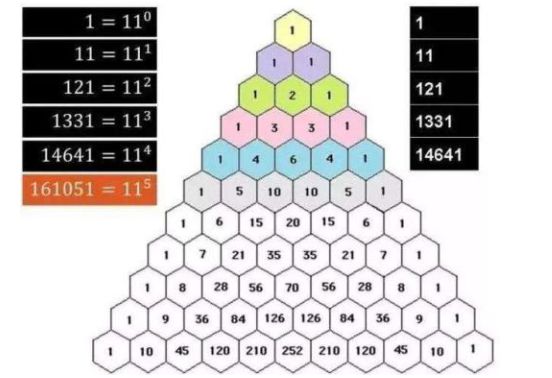
观察分子的系数,我们可以发现这里系数构成一个杨辉三角:
第一行每一个点的系数为 [1],第二行每一个点的构成元素系数为 [1,2,1],以此类推, [1,3,3,1]、[1,4,6,4,1]、[1,5,10,10,5,1] ... 其中每个点满足,即下面的元素由其上面两个元素的值相加而得:
C(n+1,i) = C(n,1) + C(n,i-1)
而分母的系数由于是不断的取二均值,所以满足:
![]()
关于为什么最终会呈现椭圆形,还需要更加严格的证明,通过上面简单的分析我们可以看到,随着迭代次数的增加,每一个点的值都会用到原始列表中的元素,且系数满足杨辉三角,最终的结果推导应该会满足一定规律,有兴趣的小伙伴可以自己动手推理一下。
四.总结
刷视频刷到了好玩的信息,虽然自己没有证明但是能够实现出来也很不错,java 写久了 python 都快忘的差不多了,实现的比较简易,有更高效的实现方法或者证明方法也欢迎大家多多交流,下面铺一下完整的代码:
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import random
import matplotlib.pyplot as plt
import os
import imageio
def getRandomPoint():
x = int(random.uniform(0, 100))
y = int(random.uniform(0, 100))
return x, y
def plotArr(pointNum=50, x_arr=[], y_arr=[], savePath=""):
if (len(x_arr) == 0 and len(y_arr) == 0):
for num in range(0, pointNum):
x, y = getRandomPoint()
x_arr.append(x)
y_arr.append(y)
x_arr.append(x_arr[0])
y_arr.append(y_arr[0])
plt.plot(x_arr, y_arr)
plt.scatter(x_arr, y_arr, c='r')
plt.savefig(savePath)
plt.cla()
return x_arr[:-1], y_arr[:-1]
else:
x_arr_new = []
y_arr_new = []
lastIndex = len(x_arr) - 1
for i in range(0, len(x_arr)):
if (i != lastIndex):
x_mid = (x_arr[i] + x_arr[i + 1]) / 2
y_mid = (y_arr[i] + y_arr[i + 1]) / 2
x_arr_new.append(x_mid)
y_arr_new.append(y_mid)
else:
x_mid = (x_arr[i] + x_arr[0]) / 2
y_mid = (y_arr[i] + y_arr[0]) / 2
x_arr_new.append(x_mid)
y_arr_new.append(y_mid)
x_arr_new.append(x_arr_new[0])
y_arr_new.append(y_arr_new[0])
plt.plot(x_arr_new, y_arr_new)
plt.scatter(x_arr_new, y_arr_new, c='r')
plt.savefig(savePath)
plt.cla()
return x_arr_new[:-1], y_arr_new[:-1]
if __name__ == '__main__':
epoch = 200
pointNum = 20
x_init = []
y_init = []
target_path = "/Users/xxx/..."
os.mkdir(target_path)
# 生成图形
frames = []
for i in range(0, epoch):
imageName = target_path + str(i) + ".jpg"
x_init, y_init = plotArr(pointNum, x_init, y_init, imageName)
frames.append(imageio.imread(imageName))
# 生成 GIF 图形
duration = 1
gifPath = target_path + "all.gif"
imageio.mimsave(gifPath, frames, 'GIF', duration=duration) # 选择'GIF'类型epoch 代表迭代次数,pointNum 代表初始化点的数量,运行结束后会在 target_path 下得到每一步的图像以及最终的 GIF 图像,快来试试吧: