基于pyspark图计算的算法实例
基于pyspark的图计算实例
- 引入
- 广度优先搜索
- 连通分量
- 强连通分量
- 标签传播
- PageRank
- 最短路径算法
- 三角形计数
引入
图算法指利用特制的线条算图求得答案的一种简便算法。无向图、有向图和网络能运用很多常用的图算法,这些算法包括:各种遍历算法(这些遍历类似于树的遍历),寻找最短路径的算法,寻找网络中最低代价路径的算法,回答一些简单相关问题(例如,图是否是连通的,图中两个顶点间的最短路径是什么,等等)的算法。图算法可应用到多种场合,例如:优化管道、路由表、快递服务、通信网站等。
GraphFrames提供与GraphX相同的标准图形算法套件以及一些新的算法。
目前,某些算法由GraphX的API实现的,因此在GraphFrames中可能没有比GraphX更可扩展的功能。
目前,我们的业务涉及到企业知识图谱,需要做路径搜索、社区发现、标签传播等基于图计算的应用,虽然neo4j也可以做,但是neo4j的分布式版本价格很高。于是考虑使用spark做分布式的图计算。
本文不介绍太多算法细节,主要展示官网和实际案例的代码实现。
广度优先搜索
广度优先搜索(Breadth-first search,简称BFS),是查找一个顶点到另外一个顶点的算法。
这里是用pyspark自带的friends数据集,实现路径搜索。
我们先看看friends数据集长啥样。
from pyspark import SparkContext
from pyspark.sql import SQLContext
from graphframes.examples import Graphs
# spark
sc = SparkContext("local", appName="mysqltest")
sqlContext = SQLContext(sc)
g = Graphs(sqlContext).friends()
g.vertices.show()
g.edges.show()
有7个节点代表7个人,然后用7个关系展示他们的人际关系,有friend和follow两种关系。
+---+-------+---+
| id| name|age|
+---+-------+---+
| a| Alice| 34|
| b| Bob| 36|
| c|Charlie| 30|
| d| David| 29|
| e| Esther| 32|
| f| Fanny| 36|
+---+-------+---+
+---+---+------------+
|src|dst|relationship|
+---+---+------------+
| a| b| friend|
| b| c| follow|
| c| b| follow|
| f| c| follow|
| e| f| follow|
| e| d| friend|
| d| a| friend|
+---+---+------------+
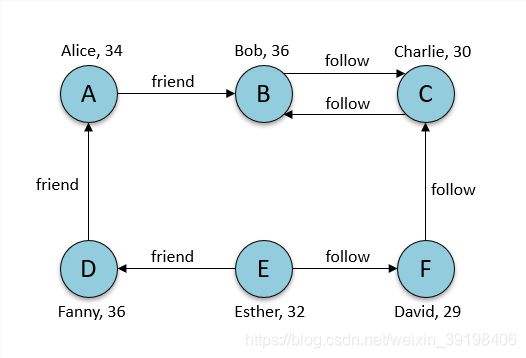
然后用BFS的API来做路径搜索,分别定义起点和终点的条件。
paths = g.bfs("name = 'Esther'", "age < 32")
paths.show()
+---------------+--------------+--------------+
| from| e0| to|
+---------------+--------------+--------------+
|[e, Esther, 32]|[e, d, friend]|[d, David, 29]|
+---------------+--------------+--------------+
可以看到,满足节点名称为Esther的有两条关系,但指向节点age小于32的只有David了,如图所示。

另外还可以使用edgeFilter限制边的条件,maxPathLength来定义链路的长度。
paths = g.bfs("name = 'Esther'", "age < 32", edgeFilter="relationship != 'friend'", maxPathLength=3)
paths.show()
+---------------+--------------+--------------+--------------+----------------+
| from| e0| v1| e1| to|
+---------------+--------------+--------------+--------------+----------------+
|[e, Esther, 32]|[e, f, follow]|[f, Fanny, 36]|[f, c, follow]|[c, Charlie, 30]|
+---------------+--------------+--------------+--------------+----------------+
同样起始条件是Esther,maxPathLength长度为3,且relationship必须不能是friend,找到下面的路径。

连通分量
连通分量(Connected Components),基于搜索算法,计算节点和节点之间能否双向抵达。
先看我们要分析的图结构。

原始数据是这样子:
people.csv
4,Dave,25
6,Faith,21
8,Harvey,47
2,Bob,18
1,Alice,20
3,Charlie,30
7,George,34
9,Ivy,21
5,Eve,30
10,Lily,35
11,Helen,35
12,Ann,35
links.csv
1,2,friend
1,3,sister
2,4,brother
3,2,boss
4,5,client
1,9,friend
6,7,cousin
7,9,coworker
8,9,father
10,11,colleague
10,12,colleague
11,12,colleague
先读取csv数据,由于csv中没有列名称也无法指定列数据类型,我们使用withColumnRenamed和withColumn来操作,也可以封装成函数方便后续使用。
from pyspark import SparkContext
from pyspark.sql import SQLContext
from graphframes import GraphFrame
from graphframes.examples import Graphs
# spark
sc = SparkContext("local", appName="mysqltest")
sc.setCheckpointDir("./ccpoint")
sqlContext = SQLContext(sc)
# g = Graphs(sqlContext).friends() # Get example graph
# 读取数据
links_df = sqlContext.read.csv("links.csv")
# 修改列名称
links_df = links_df.withColumnRenamed("_c0", "src")\
.withColumnRenamed("_c1", "dst")\
.withColumnRenamed("_c2", "relationship")
# 修改列类型
links_df = links_df.withColumn("src", links_df["src"].astype("int"))\
.withColumn("dst", links_df["dst"].astype("int"))
links_df.show()
# 读取数据
nodes_df = sqlContext.read.csv("people.csv")
# 修改列名称
nodes_df = nodes_df.withColumnRenamed("_c0", "id")\
.withColumnRenamed("_c1", "name")\
.withColumnRenamed("_c2", "age")
# 修改列类型
nodes_df = nodes_df.withColumn("id", nodes_df["id"].astype("int"))\
.withColumn("age", nodes_df["age"].astype("int"))
nodes_df.show()
+---+---+------------+
|src|dst|relationship|
+---+---+------------+
| 1| 2| friend|
...
+---+-------+---+
| id| name|age|
+---+-------+---+
| 4| Dave| 25|
...
然后使用内置Connected Components算法计算。
g = GraphFrame(nodes_df, links_df)
result = g.connectedComponents()
result.select("id", "component").orderBy("component").show()
输出节点的分组信息:
+---+---------+
| id|component|
+---+---------+
| 2| 1|
| 4| 1|
| 8| 1|
| 7| 1|
| 9| 1|
| 5| 1|
| 1| 1|
| 6| 1|
| 3| 1|
| 10| 10|
| 11| 10|
| 12| 10|
+---+---------+
强连通分量
from pyspark import SparkContext
from pyspark.sql import SQLContext
from graphframes import GraphFrame
from graphframes.examples import Graphs
# spark
sc = SparkContext("local", appName="mysqltest")
sc.setCheckpointDir("./ccpoint")
sqlContext = SQLContext(sc)
g = Graphs(sqlContext).friends()
result = g.stronglyConnectedComponents(maxIter=10)
result.select("id", "component").orderBy("component").show()
标签传播
标签传播算法(Label Propagation Algorithm,简称LPA),用来检测网络中的社区。
LPA不能保证会收敛,也可能会使每个节点都被识别为一个社区,但是计算消耗的资源很低廉。
from pyspark import SparkContext
from pyspark.sql import SQLContext
from graphframes import GraphFrame
from graphframes.examples import Graphs
# spark
sc = SparkContext("local", appName="mysqltest")
sc.setCheckpointDir("./ccpoint")
sqlContext = SQLContext(sc)
g = Graphs(sqlContext).friends()
result = g.labelPropagation(maxIter=5)
result.select("id", "label").show()
PageRank
PageRank的可以计算节点的权重排名。应用场景有很多,最著名的就是网页排名,还有以下应用场景:
- Twitter:个性化PageRank算法用于向用户推荐他们可能希望关注的账号。
- 用于给公共场所和街道排名,同时预测街道和人类的活动趋势。
- 在医疗和保险行业,作为欺诈探测系统,帮助医生或者供应商发现异常行为,并将其作为负样本给机器学习算法进行训练。

from pyspark import SparkContext
from pyspark.sql import SQLContext
from graphframes import GraphFrame
from graphframes.examples import Graphs
# spark
sc = SparkContext("local", appName="mysqltest")
sc.setCheckpointDir("./ccpoint")
sqlContext = SQLContext(sc)
g = Graphs(sqlContext).friends()
results = g.pageRank(resetProbability=0.15, tol=0.01)
results.vertices.select("id", "pagerank").show()
results.edges.select("src", "dst", "weight").show()
results2 = g.pageRank(resetProbability=0.15, maxIter=10)
results3 = g.pageRank(resetProbability=0.15, maxIter=10, sourceId="a")
results4 = g.parallelPersonalizedPageRank(resetProbability=0.15, sourceIds=["a", "b", "c", "d"], maxIter=10)
最短路径算法
最短路径,顾名思义,两点之间最短可到达方式。
shortestPaths计算的是图中每个顶点到landmarks中给定的顶点的最短路径。
from pyspark import SparkContext
from pyspark.sql import SQLContext
from graphframes import GraphFrame
from graphframes.examples import Graphs
# spark
sc = SparkContext("local", appName="mysqltest")
sc.setCheckpointDir("./ccpoint")
sqlContext = SQLContext(sc)
g = Graphs(sqlContext).friends()
results = g.shortestPaths(landmarks=["a", "d"])
results.select("id", "distances").show()
+---+----------------+
| id| distances|
+---+----------------+
| b| []|
| e|[d -> 1, a -> 2]|
| a| [a -> 0]|
| f| []|
| d|[d -> 0, a -> 1]|
| c| []|
+---+----------------+
三角形计数
三角形计数(Triangle count)一般用来分析社交网络。
通过Triangle Count能够提供集群的度,是进行聚类分析的重要依据和指标。
from pyspark import SparkContext
from pyspark.sql import SQLContext
from graphframes import GraphFrame
from graphframes.examples import Graphs
# spark
sc = SparkContext("local", appName="mysqltest")
sc.setCheckpointDir("./ccpoint")
sqlContext = SQLContext(sc)
g = Graphs(sqlContext).friends()
results = g.triangleCount()
results.select("id", "count").show()
