基于BP神经网络实现气凝胶加气混凝土抗压强度预测（附代码）

目录

前言

1. 背景

1.1 什么是加气混凝土 

1.2 传统AAC抗压强度测试方法

1.3 为什么选择BP神经网络 

2. MATLAB算法实现

2.1 训练集数据编辑

2.2 数据导入与整理

2.3 BP神经网络建立

3. 算法评价

3.1 算法运行结果

3.2 本算法的不足和待改进之处

 3.2.1 BP神经网络学习不稳定

 3.2.2 预测多个数据时出现预测值相同的情况

 3.2.3 该网络对数据的质量要求高

 3.2.4 每个自变量对于结果的影响程度不同

4. 总结 

附：MATLAB源代码

---

前言

随着人工智能技术的不断发展，各种AI产品已经逐步进入了我们的生活。土木工程作为一门古老的学科，亟需赶上时代的步伐，本文以一种轻质的加气混凝土砌块抗压强度预测为例，利用BP神经网络寻求简化传统复杂的试件制备工作，取得了较好的预测效果。

1. 背景

1.1 什么是加气混凝土 

加气混凝土（AAC）是以硅质材料（砂、粉煤灰及含硅尾矿等）和钙质材料（石灰、水泥）为主要原材料，掺加化学发气剂（铝粉），通过配料、搅拌、浇注、静停发气、预养、切割、蒸压、脱模、养护等工艺过程制成的轻质多孔硅酸盐制品。在外观上，相比普通混凝土，AAC有着更大更多的孔洞，这也使它具有出色的保温隔热能力，广泛应用于建筑行业。

​ 100mm×100mm×100mm立方体加气混凝土试件

​ 加气混凝土外表面发气过程

1.2 传统AAC抗压强度测试方法

传统AAC抗压强度测试需要按照国家规范制备试件若干组，每组三个，在研究因素较多时制模数量巨大，养护时间长，需要大量的材料、设备、时间和人工。

1.3 为什么选择BP神经网络 

我们知道有线性回归、支持向量机、随机森林、神经网络等一系列经典的预测算法。选择BP神经网络进行预测是因为它具有较强的自主学习和自主预测的能力，可调整的参数较多，泛化能力较强，容错能力较强。本问题实质为一个简单的预测问题， 应使预测结构尽量简单，同时又要保证结果的准确性。

---

2. MATLAB算法实现

2.1 训练集数据编辑

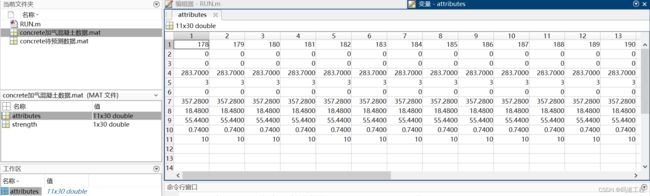
Step1：将文件 concrete加气混凝土数据.mat 导入Matlab

Step2：修改训练集数据

attributes表示混凝土的成分组成，（按行排列默认原材料1.水泥、2.矿粉、3.粉煤灰、4.水、5.外加剂、6.碎石、7.砂、8.石膏、9。石灰、10.铝粉、11.气凝胶的用量，单位g），当未掺加该组分时输入0；strength表示混凝土抗压强度（单位MPa）。

​ 加气混凝土试件组分参数训练集

Step3：保存数据

在Matlab左侧工作区选择训练集变量（Ctrl同时选择attributes和strength），右键另存为，覆盖原文件保存。

​

注：（1）同一容重、同一类型的加气混凝土数据才有预测价值。

       （2）测试集和待预测数据集的编辑方法同上。

       （3）训练数据集中的数据不能过少。

2.2 数据导入与整理

Step4：清空页面

clear all
clc
close all

Step5：导入加气混凝土试件数据

导入数据时将左侧文件夹打开至文件保存路径。

load concrete加气混凝土数据.mat;
load concrete待预测数据.mat; 

Step6：数据整理

用简单的字符代替复杂的文件名。

A=attributes;      %简化组分变量名为A
B=strength;        %简化强度变量名为B
C=A';              %组分矩阵转置
D=B';              %强度矩阵转置
E=attributes2;     %简化待预测组分变量名为E
F=E';              %待预测组分矩阵转置

Step7：划分训练集和测试集

randperm随机整数生成和随机打乱矩阵顺序，使数据没有规律性，size（c，1）表示矩阵c的行数，size（c，2）表示矩阵C的列数。

这里共设置了30个数据，我们让前20个数据作为训练集，后10个数据作为测试集。（数据划分可自行调整）

G = randperm(size(C,1)); 
P_train = C(G(1:20),:)';      %组分训练集——20个样本
T_train = D(G(1:20),:)';      %强度训练集——20个样本
P_test = C(G(20:end),:)';     %组分测试集——10个样本
T_test = D(G(20:end),:)';     %强度测试集——10个样本
N = size(P_test,2);           %提取组分测试集的列数，即组分测试集的样本数

Step8： 数据归一化

数据归一化即把全部数据转化为0-1之间的数值，这样可以加快梯度下降求最优解的速度，加快收敛。（归一化后的数据名称在此都用小写表示）

[p_train, p_input] = mapminmax(P_train,0,1);      %组分训练集归一化，以p_train作为输出
p_test = mapminmax('apply',P_test,p_input);       %组分测试集归一化，以p_test作为输出
[t_train, p_output] = mapminmax(T_train,0,1);     %强度训练集归一化，以t_train作为输出

2.3 BP神经网络建立

Step9：创建BP神经网络

利用归一化后的组分训练集和强度训练集创建神经网络，这里的1为采用单层单神经元的网络架构。（1输入层、1隐藏层、1输出层 ）

net = newff(p_train,t_train,1);
W1= net. iw{1, 1};                  %输入层到隐藏层的权值
B1 = net.b{1};                      %隐藏层神经元阈值
W2 = net.lw{2,1};                   %隐藏层到输出层的权值
B2 = net. b{2};                     %输出层神经元阈值

​ BP神经网络架构

Step10：设置训练参数 

学习率的选择这里采用人工调整学习率，根据经验值进行尝试，通常将初始学习率设为：0.1，0.01，0.001，0.0001。

net.trainParam.epochs = 1000;      %设置训练次数为1000
net.trainParam.goal = 1e-3;        %设置均方误差
net.trainParam.lr = 0.0001;        %设置学习率

Step11：训练神经网络

net = train(net,p_train,t_train);

Step12：仿真测试

t_sim = sim(net,p_test);      %利用Simulink函数将组分测试集归一化后的数据输入网络进行测试

Step13：数据反归一化

由于输入神经网络的数据为归一化的数据，输出时要展示原始类型数据，故要进行数据反归一化处理。

T_sim = mapminmax('reverse',t_sim,p_output); 

Step14：计算相对误差

相对误差用于反映测量的可信程度，这里表示原始数据与反归一化后数据的误差。

error = abs(T_sim - T_test)./T_test;

Step15：计算决定系数R²

决定系数R²介于0~1之间，用于评判拟合效果。当 R²越接近1，回归拟合效果越好，我们一般认为超过0.8的模型拟合优度比较高。

R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 

Step16：结果对比

以矩阵形式输出强度测试集、反归一化强度测试集、相对误差。（这里句末不加分号目的是让结果直接输出在命令行窗口）

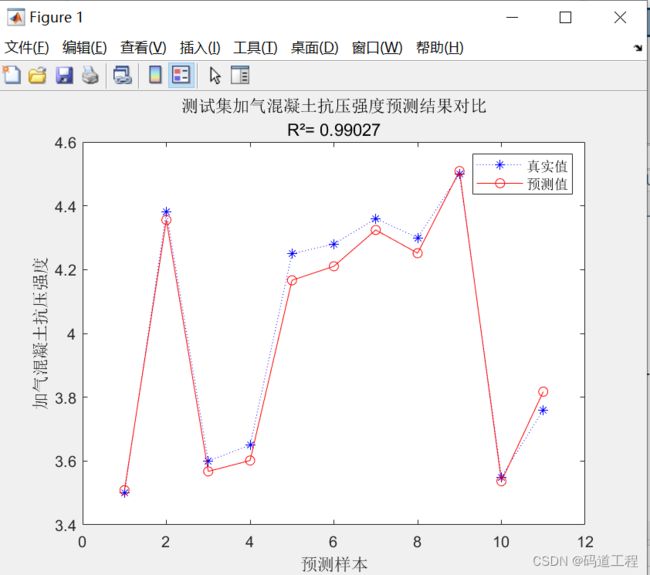
result = [T_test' T_sim' error']

Step17：绘制训练及测试效果图

figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('加气混凝土抗压强度')
string = {'测试集加气混凝土抗压强度预测结果对比';['R²= ' num2str(R2)]};   %num2str()将数字转为字符
title(string)

Step18：新数据预测

predict_y = zeros(1,1);       %初始化预测矩阵
P_result = sim(net, F(1,:)');   
predict_y = P_result;
predict_y = mapminmax('reverse',predict_y,p_output);      %反归一化处理
disp('预测值为：')
disp(predict_y)

---

3. 算法评价

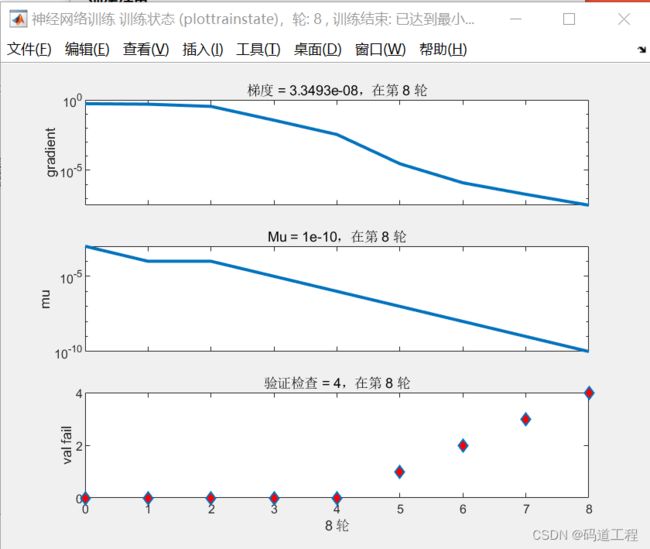
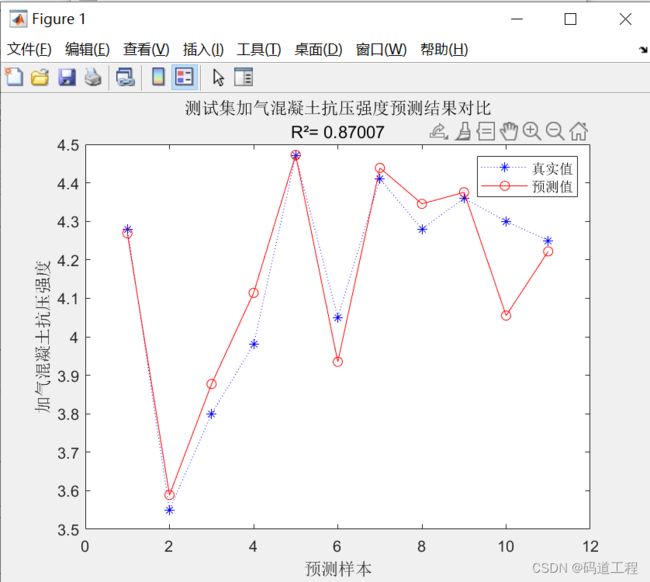
3.1 算法运行结果

由运行结果可知，本套算法采用莱文贝格－马夸特训练方法经过8轮迭代，达到最小梯度。决定系数R²为0.98207，R²接近1，回归拟合效果较好，对于新数据的预测经实验检验也较为准确。

​ 测试结果矩阵

​

​ 测试集加气混凝土抗压强度预测结果对比图

​ 神经网络训练

​ 神经网络训练性能

​ 神经网络训练状态

​ 神经网络回归结果

3.2 本算法的不足和待改进之处

本套算法是比较基础的预测方法，使用的架构也是浅层神经网络，作为新手一种初步的尝试和学习，可能存在较多不合理之处，望各位大佬批评指正。下面简单说一下我在设计时遇到的一些问题。

3.2.1 BP神经网络学习不稳定

从下图中可以看出，每次运算得到的决定系数R²很不稳定，拟合效果差异较大。

​

 ​

3.2.2 预测多个数据时出现预测值相同的情况

当采用下面循环语句进行预测时，出现了预测值相同的情况。（请各位大佬指点）

predict_y = zeros(8,1);       %初始化预测矩阵
for i = 1: 8
    P_result = sim(net, F(i,:)');   
    predict_y(i) = P_result;
    predict_y(i) = mapminmax('reverse',predict_y(i),p_output);    %反归一化处理
end
    disp('预测值为：')
    disp(predict_y)

3.2.3 该网络对数据的质量要求高

当数据间的差异稍大时，拟合结果就会出现不小的波动。

​

3.2.4 每个自变量对于结果的影响程度不同

加气混凝土是一种较为精细的混凝土，铝粉和气凝胶掺量是加气混凝土中重要的参数，1-2g的误差都会使抗压强度产生巨大的变化。另外，水、水泥也对抗压强度起着重要的作用。如何将这个问题考虑进去值得思考。

---

4. 总结 

本文以一种轻质的加气混凝土砌块抗压强度预测为例，利用BP神经网络寻求简化传统复杂的试件制备工作，取得了较好的预测效果。但由于本人正处于初步探索和学习阶段，算法可能会存在一些问题，并且在实际的使用过程中还需要更深入的设计，需要考虑得更加全面，希望能和各位同仁互相学习，给我提出宝贵的建议。

---

附：MATLAB源代码

%% 基于BP神经网络实现加气混凝土抗压强度预测MATLAB源代码 

%% 1.清空数据
clear all
clc
close all

%% 2.导入加气混凝土数据
load concrete加气混凝土数据.mat;     %训练数据越多，预测越精准
load concrete待预测数据.mat;         %导入待预测数据

%% 3.数据整理
A=attributes;             %简化组分变量名
B=strength;               %简化强度变量名
C=A';                     %组分矩阵转置
D=B';                     %强度矩阵转置
E=attributes2;            %简化待预测组分变量名为E
F=E';                     %待预测组分矩阵转置

%% 4.划分训练集和测试集
G = randperm(size(C,1));     %randperm随机整数生成和随机打乱矩阵顺序，使数据没有规律性，size（c，1）表示矩阵c的行数，size（c，2）表示矩阵C的列数
P_train = C(G(1:20),:)';     %组分训练集——20个样本
T_train = D(G(1:20),:)';     %强度训练集——20个样本
P_test = C(G(20:end),:)';    %组分测试集——10个样本
T_test = D(G(20:end),:)';    %强度测试集——10个样本
N = size(P_test,2);          %提取组分测试集的列数，即组分测试集的样本数

%% 5.数据归一化
[p_train, p_input] = mapminmax(P_train,0,1);       %组分训练集归一化，以p_train作为输出
p_test = mapminmax('apply',P_test,p_input);        %组分测试集归一化，以p_test作为输出
[t_train, p_output] = mapminmax(T_train,0,1);      %强度训练集归一化，以t_train作为输出

%% 6.创建BP神经网络
net = newff(p_train,t_train,3);     %利用归一化后的组分训练集和强度训练集创建神经网络，这里的1为采用单层单神经元的网络架构
W1= net. iw{1, 1};                  %输入层到隐藏层的权值
B1 = net.b{1};                      %隐藏层神经元阈值
W2 = net.lw{2,1};                   %隐藏层到输出层的权值
B2 = net. b{2};                     %输出层神经元阈值

%% 7.设置训练参数
net.trainParam.epochs = 1000;       %设置训练次数为1000
net.trainParam.goal = 1e-3;         %设置均方误差
net.trainParam.lr = 0.0001;         %学习率的选择这里采用人工调整学习率，根据经验值进行尝试，通常将初始学习率设为:0.1，0.01，0.001，0.0001

%% 8.训练神经网络
net = train(net,p_train,t_train);

%% 9.仿真测试
t_sim = sim(net,p_test);          %利用Simulink函数将组分测试集归一化后的数据输入网络进行测试

%% 10.数据反归一化
T_sim = mapminmax('reverse',t_sim,p_output);      %由于输入神经网络的数据为归一化的数据，输出时要展示原始类型数据，故要进行数据反归一化处理

%% 11. 性能评价（相对误差error）
error = abs(T_sim - T_test)./T_test;       %相对误差用于反映测量的可信程度，这里表示原始数据与反归一化后数据的误差。

%% 12. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));        
%决定系数R²介于0~1之间，用于评判拟合效果。当 R²越接近1，回归拟合效果越好，我们一般认为超过0.8的模型拟合优度比较高

%% 13. 结果对比
result = [T_test' T_sim' error']      %以矩阵形式输出强度测试集、反归一化强度测试集、相对误差

%% 14. 绘制训练及测试效果图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('加气混凝土抗压强度')
string = {'测试集加气混凝土抗压强度预测结果对比';['R²= ' num2str(R2)]};     %num2str()将数字转为字符
title(string)

%% 15. 新数据预测
predict_y = zeros(1,1);          %初始化预测矩阵
P_result = sim(net, F(1,:)');   
predict_y = P_result;
predict_y = mapminmax('reverse',predict_y,p_output);         %反归一化处理
disp('预测值为：')
disp(predict_y)