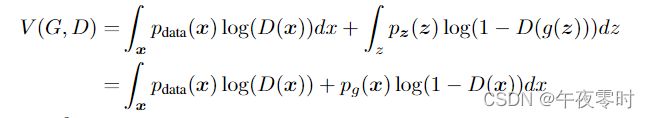GAN——Generative Adversarial Nets生成对抗网络总结
1.摘要Abstract
对抗网络模型新框架：
- G：generater生成器——优化目标是最大化D出错的概率
- D：discriminater鉴别器——优化目标是准确识别原始数据还是G的生成数据
这个框架对应于一个极小极大的两人博弈。在任意函数G和D的空间中，存在唯一的解，其中G恢复训练数据分布，D处处等于1 2。
2. 介绍Instruction
鉴别器由于反向传播算法有很好的表现，成果很多
生成器仍存在诸多限制
- 难以计算最大似然估计和相关策略中出现的许多难以处理的概率估计
- 难以利用分段线性单元处理的梯度优势
G和D使用的模型：多层感知机MLP和dropout法
3.相关工作 Related Work
方式一：最大化对数似然来训练模型
代表：deep Boltzmann machine
方式二：变分自动编码器variational autoencoders (VAEs)
与生成性对抗网络不同，VAE中的第二个网络是执行近似推理的识别模型
方式三：使用判别标准来训练生成模型
使用固定噪声中用来识别数据的那些权重来训练生成器
方式四：可预测性最小化
- 在训练其他网络时，G要保持独立
- 一个网络试图使输出相似，另一个网络试图使输出不同
- 优化目标是最小化目标函数
对抗性示例，即人类无法感知出区别的两个样本，模型却十分自信的给出不同的分类，证明现代的分类器网络并不是在模仿人类的感知属性，而是学习到一套自己的判断类别的属性。
4. 对抗网络Adversarial Nets
4.1值函数V（D，G）
D(x; θd)：带有可学习参数θd的模型D，将输入x判断为来自于真实数据(1)还是生成数据(0)，注意这里给出的是一个介于0-1之间的数，越接近于1，则判断为真实数据，越接近0则判断为生成数据
G(z; θg)：带有可学习参数θg的模型G，将输入的噪音z生成模仿数据x分布的G(z)
对于minG，从值函数V(D，G)考虑，如果D(G(z))被判断为1(真实数据的标签)，则对于log[1 - D(G(z))]的值为负无穷，故最小化G意味着使得所有G(z)被判断为真实数据，即生成的数据要能瞒过鉴别器
对于maxD，从值函数V(D，G)考虑，如果D(G(z))被判断为0(生成数据的标签)，D(x)被判断为1(真实数据的标签)，对于log(D(X))，则值为0，对与log[1 - D(G(z))]值也为0，为V(D,G)的最大值，所以最大化D意味着鉴别器能准确分辨出两类数据，不会被生成器所欺骗。
4.2图示
蓝色虚线：鉴别器的函数
黑色点线：真实数据生成的分布
绿色实线：生成器的数据分布
底下爱的平行直线：均匀采样的噪声分布z， 和数据分布x
箭头：从z到x的映射
图（a）———刚开始生成数据的分布与原始数据的分布很像，分类器的正确率还不高
图（b）———D被跟新为收敛于D∗(x) =p (x)/[p (x)+p(g(x))]
图（c）———对G更新，D的梯度流向G，指导G的数据分布像原数据靠拢
图（d）———经过几轮更新，达到一个最优值，两个分布相等，分类器无法区分二者
4.3实践表明
训练早期，D的效果非常好训练很快，导致D(G(x))所得的值接近于0，即值函数log[1 - D(G(z))]项变得很小，使得对G的误差反向传播很慢，因此使用log[D(G(z))]得到接近负无穷的数，利于反向传播，同时模型的最优解不变。然而一个接近负无穷的数又会带来数值表示等的一些问题，在本篇文章中未给出说明。
5.理论
算法：
对D做K步更新，使D接近与当前的给定的G的最优解，然后对G做一步更新，使G更接近原始数据分布。
5.1全局最优解
证明1：固定G，最优的D分布
。
对值函数算期望并合并
p与D无关，将D(x)写为y，则上式为 alog(y) + blog(1 −y)，其最大值点在a / (a + b)。
当D*(X)固定时， V（G，D）写为C（G）：
定理：C(G)达到最小值，当且仅当，且值为-log(4)
证明2：
5.2算法的收敛性
当G和D有足够的容量时，并且在算法的每一步都允许给定G的最优的D，当G按照公式更新时，最终Pg收敛到Pdata。
证明：由于D已经是最优，故将V(G, D) = U(Pg, D)，
，此时优化Pg(X)。由于Pg(X)是一个凸函数，所以是Pg(X)的函数，也是凸函数。故U(Pg, D)的上界函数也是凸函数，其最优解已经在5.1给出证明。
原文：
Ian Goodfellow et al. “Generative Adversarial Nets” Neural Information Processing Systems (2014)shishi