深度学习课程笔记(三)Backpropagation 反向传播算法
2017.10.06
材料来自:http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS17.html
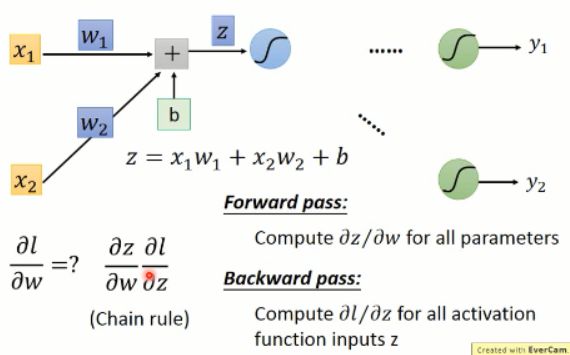
反向传播算法这里是用到 chain rule(链式法则)的,如下图所示:
这个应该没什么问题。大家都学过的。
我们知道总的loss 是由各个小的 loss 组合得到的,那么我们在求解 Loss 对每一个参数的微分的时候,只要对每一个 loss 都这么算就可以了。那么我们以后的例子都是以 loss 的为基础而来的。
这里我们的反向传播,主要依赖于前向传播和反向传播,其loss的计算也是依赖于链式法则:
有了上面 z 的表达式,我们分别对 w1 和 w2 进行求导,我们可以得到对应的结果,分别为: x1 and x2。其实就是连接权重的输入。
那么,很直观的,我们可以得到如下的结果:
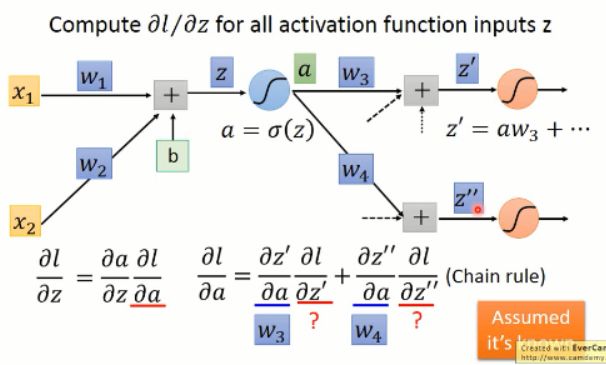
OK,现在我们求解出其中的一项了,那么,另外一项该怎么算呢?我们接着看:
这里的激活函数 a,我们用的 sigmoid,当然也可以是其他的函数了。我们对该激活函数进行求导,可以得到其微分,这个就是该项的左侧部分,那么右侧该怎么算呢?
我们知道,后面有可能又有很多的 layer,该结果可能影响后面所有的值。我们假设这里只有 2 个神经元,那么我们可以得到:
我们将右边那一项按照链式法则展开后,可以发现,又是这样子,输出对变量求导后就是输入,所以,展开后的两项的稀疏,都是已知的输入,即:w3 and w4。那么另外两项分别是什么呢?其实这个又是和后续有关的,这里我们假设这些值是已知的,那么我们就可以算出右侧的值了。
那么 l 对 z 求偏导之后的值,我们可以计算出来:
这里,其实有两种情况:
1. 此处是最后一层,那么我们就可以直接计算就行了:
2. 若不是最后一层呢?我们只要将后面计算出的值,带入到这里就行了。
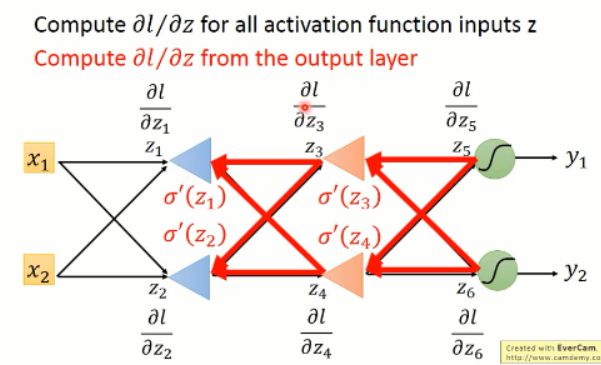
以上部分,是从输入端开始算起,所以每次都会遇到利用后面的值的问题,貌似计算量很大啊。。怎么办?
其实,没必要的啦,我们可以后面向前算,我们知道了后面的 loss,我们去求前一层的各种偏导数,然后依次向前算,就可以得到整个网络的各个偏导数的值啦。。。。
也就是说:
所以,这个过程其实就是反向传播算法啦。。。总结一下:
通过这样子的方法,我们得到了其偏微分,其实就是梯度啦。。。根据梯度下降的方法,我们就可以更改权重,使得 loss 最小,从而就完成了神经网络的训练。。。。