图像去雾及Matlba实现

图像去雾及Matlab实现

一、暗通道先验及求解推导

  对于图像去雾算法，最经典且实现效果最好的便是何凯明博士的暗通道去雾算法，其算法原理基于暗通道先验，即在绝大多数非天空的图像区域内，总存在某一些像素的至少一个颜色通道有一个很低的值。其数学定义如下，对于任意输入图像$J$，其暗通道为：
$$J^{dark}(x)=\underset{y\in \Omega (x)}{\min }(\underset{c\in \{r,g,b\}}{\min }(J^c(y))$$简而言之，便是计算一副图像的每一个像素点的RGB三个通道中的最小值，存入一副与原始图像大小相同的灰度图中，再对这副灰度图进行最小值滤波，所得到的所有点的最小值即定义为$J^{dark}$，何凯明博士通过对大量图像的实验，发现$J^{dark}$几乎都是一个很小的值。故暗通道先验理论指出：
$$J^{dark}\to 0$$  实际生活中造成暗原色中低通道值主要有三个因素：a)汽车、建筑物和城市中玻璃窗户的阴影，或者是树叶、树与岩石等自然景观的投影；b)色彩鲜艳的物体或表面，在RGB的三个通道中有些通道的值很低,比如绿色的草地，红色或黄色的花朵，或者蓝色的水面；c)颜色较暗的物体或者表面，例如灰暗色的树干和石头。总之，自然景物中到处都是阴影或者彩色，这些景物的图像暗原色总是很灰暗的。
  此处选用最小值滤波半径为7，其暗通道求解Matlab代码如下：

function win_dark = getdarkimg(I)
%% 暗通道求解代码
% 参数I为原图像
% 输出win_dark为暗通道图
[h, w, ~] = size(I);  		
win_size = 0;               % 滤波半径     
win_dark = ones(h, w);      % 暗通道图像
 
%计算分块深度darkchannel
for j = 1 + win_size : w - win_size
    for i = win_size + 1 : h - win_size
        m_pos_min = min(I(i, j, :));
        for n = j - win_size : j + win_size    
            for m = i - win_size : i + win_size
                if (win_dark(m, n) > m_pos_min)
                    win_dark(m, n) = m_pos_min;
                end
            end
        end
    end
end

取部分图像计算其暗通道结果如下：

通过上图可看出，在有雾区域，其暗通道灰度值往往较高，并且上述例子中，也可看出暗通道先验理论的普遍性，即一幅图像中往往有$J^{dark}\to 0$。而对于无雾图像的暗通道图像，此处亦找了一些图像，计算得到对应的暗通道图像如下：

通过上图，更加可以看出暗通道理论的普遍性，同时也可以发现，天空情景下对应的暗通道与有雾区域的相似，即灰度值不接近0，这也印证了为什么初代暗通道先验算法对于图像去雾的应用中，对于天空、大范围留白图片不适用的结论。有了暗通道先验的相关认识，接下来便是进行一些数学推导，以找出有雾图像与去雾图像之间的转换关系。
  在较为传统的雾天图像退化模型描述中，有雾图像的定义如下：
$$I(x)=J(x)e^{-rd(x)}+A(1-e^{-rd(x)})$$ 其中$I$为所观察到的有雾图像，$J$为待恢复的无雾图像，$A$为全局大气光成分，$r$为大气散射系数，$d$为景物深度。其中$A$一般设定与空间坐标无关。$e^{-rd(x)}$即代表空间坐标$x$处的透射率，使用$t(x)$代替，则上式可转变为：
$$I(x)=J(x)t(x)+A(1-t(x))$$上式其实较容易理解，有雾图像即为原景观与大气光的线性组合。通过上式便可转换得到待恢复的无雾图像的表达式为：
$$J^c(x)=\frac{I^c(x)-A^c}{t(x)}+A^c$$  在观察图像$I$已知的情况下，要实现图像去雾便需要求解大气光成分$A$以及$x$处的透射率$t(x)$。

二、大气光成分A的求解

  在论文中提到对于大气光成分$A$的求解借助于暗通道图，其步骤如下：

1. 从暗通道图中按照亮度的大小取前0.1%的像素，即取前0.1%个较大值；
2. 在这些像素所对应的原始有雾图像中，寻找对应具有最高亮度的像素点，即RGB三通道数值的加权平均最大的像素点，以该像素点的RGB数值担任大气光成分A。

通过上述求解即可得到大气光成分$A$的取值，其Matlab代码如下。

function A = getLight(darkimg, srcimg)
%% 计算大气光值A
% 参数darkimg为图像暗通道图，参数srcimg为原图像
% 输出A为大气光成分
[h, w] = size(darkimg);
darksize = h * w;
topsize = darksize / 1000;
A = zeros(1, 3);

darkcopy = darkimg(:);
[~, index] = sort(darkcopy, 'descend');
max = 0;
for i = 1 : topsize
    row = rem(index(i), h);
    col = ceil(index(i) / h);
    if (row == 0)
        row = h;
    end
    nowavg = (srcimg(row, col, 1) + srcimg(row, col, 2) + srcimg(row, col, 3)) / 3;
    if (max < nowavg)
        max = nowavg;
        A = [srcimg(row, col, 1), srcimg(row, col, 2), srcimg(row, col, 3)];
    end
end

三、透射率t(x)的求解

  上述假设前提下，大气光成分$A$与空间坐标无关，即为一个大于0的常向量，因此若等式两端同时除以$A^c$，即大气光成分RGB通道中的任意一个，则有：
$$\frac{I^c(x)}{A^c}=\frac{J^c(x)}{A^c}t(x)+(1-t(x))$$其中上标$c$表示RGB三个通道中的任意一个通道，若对上式应用暗通道先验结论，则需要对等式两边求两次最小值运算，如下式所示：
$$\underset{y\in \Omega (x)}{\min }(\underset{c}{\min }\frac{I^c(y)}{A^c})=\underset{y\in \Omega (x)}{\min }(\underset{c}{\min }\frac{J^c(x)}{A^c}t(x))+(1-t(x))$$根据上述按通道先验理论有：
$$J^{dark}(x)=\underset{y\in \Omega (x)}{\min }(\underset{c}{\min }(J^c(y))=0$$则可得：
$$\underset{y\in \Omega (x)}{\min }(\underset{c}{\min }\frac{J^c(x)}{A^c}t(x))=0$$设空间坐标$x$处的投射率为$\tilde{t}(x)$，则：
$$\tilde{t}(x)=1-\underset{y\in \Omega (x)}{\min }(\underset{c}{\min }\frac{I^c(y)}{A^c})$$即利用暗通道先验结论，即可求解空间坐标$x$处的透射率$t(x)$。通过上述暗通道示例已知，暗通道不是天空、大面积留白区域合适的先验，但幸运的是，在有雾图像中，天空与大气光A非常相似，则有：
$$\underset{y\in \Omega (x)}{\min }(\underset{c}{\min }(\frac{I^c(y)}{A^c}))\to 1,\tilde{t}(x)\to 0$$  由于天空在无限远处，则透射率趋近于0，因此锁推导的待恢复无雾图像也是可以满足的。同时，考虑到视觉效果，完全去除雾霾会使图像看起来不自然且丢失了深度信息，因此选择对雾霾进行少量的保存，则在上述投射率的计算公式中引入了恒参$w$，一般取$w=0.95$：
$$\tilde{t}(x)=1-w\underset{y\in \Omega (x)}{\min }(\underset{c}{\min }\frac{I^c(y)}{A^c})$$即实现了透射率的求解。仍旧采用上述示例，利用上述推导，求得图像的透射率图如下：

通过上图可看出，此时所求得的透射率整体上符合初始观察图片中的雾霾的分布情况，但同时也可看出，此时的透射率结果是较为粗糙的，如上图中树叶处的处理并不满足人意，即丧失了边缘信息。若以此时的透射率直接进行求解，则所得到的去雾结果如下：

通过上图非常容易看出，通过上述推导实现的图像去雾算法对于边缘的实现效果非常差。无论是树林与天空的交界处，还是天安门建筑的屋顶都不是那么的满足观感，因此需要对所求得的透射率进行细化以获得更好的结果。何凯明博士提出图像软抠图与导向滤波两种方法，其中图像软抠图因为其耗时过长，虽然最终实现结果较好，但不能满足实际应用；而导向滤波便有着较快的实现速度与不赖的图像去雾结果，故下文将对导向滤波进行介绍。此处实现的Matlab代码如下。

function R = anyuanseGF(m_img, win_dark)
%% 求解去雾图像
% 参数m_img为原图像，参数win_dark为暗通道图
% 输出R为去雾图像
I = double(m_img) / 255;
[h, w, ~] = size(I);  
img_size = h * w;

% 大气光求解
A = getLight(win_dark, I);
avgA = sum(A) / 3;
% 透射率求解
for cc = 1 : img_size
    win_dark(cc) = 1 - 0.95 * (win_dark(cc) / avgA);
end

% 利用导向滤波细化透射率，此处可先略过这一函数调用
win_dark = guidedfilter(rgb2gray(I), win_dark, 50, 0.0001);

% 计算原图像
R = zeros(h, w ,3);
for i = 1 : 3
    for j = 1 : h
        for l = 1 : w
            R(j, l, i) = (I(j, l, i) - A(i)) / win_dark(j, l) + A(i);
        end
    end
end

三、导向滤波细化透射率

  对于噪声和边缘的区别，噪声一般周围的像素梯度变化较大，并且以其为中心，向四周的梯度大体相似。而边缘出现了梯度的阶跃，并且梯度最大的方向在边缘的法线方向，其他方向远离法线方向逐渐变小。一般的滤波无法区分噪声和边缘，于是对其统一处理，因此很多情况下，滤波的同时，边缘也被处理模糊了。故导向滤波的提出便是为了解决边缘模糊问题。

从图中可以看出，导向滤波的输入有两个，一个是原始图像$p$，一个是引导图象$I$，其中引导图像$I$可与原始图像$p$相同。输出为$q$，即：
$$q_i=\sum W_{ij}(I)\cdot p_j$$该公式中$W_{ij}(I)$为$p_j$加权平均时所用到的权值，该滤波器相对于$p$时线性的。导向滤波的一个重要假设是输出图像和引导图像在滤波窗口上存在局部线性关系，即：
$$q_i=a_k{I}_i+b_k,\forall i\in w_k$$对于一个以$r$为半径的确定的窗口$w_k$，其所对应的$a_k、b_k$也将是唯一确定的常量系数，这就保证了在一个局部区域内，如果引导图像$I$有一个边缘的时候，输出图像$q$也保持边缘不变性，因为对于响铃的像素点而言，存在$\nabla q=a\nabla I$，即引导图像存在梯度的像素点处，输出图像也会存在梯度，即保证了边缘的保留。同时，认为输入图像中非边缘区域又不平滑的地方为噪声$n$，因此有$q_i=p_i-n_i$，最终目标便是最小化这个噪声，则其最小二乘表示为：
$$argmin\sum _{i\in w_k}(q_i-p_i{)}^2=argmin\sum _{i\in w_k}(a_k{I}_i+b_k-p_i{)}^2$$最后，引入一个正则化参数$ϵ$避免$a_k$过大，即需要保证输出图像与引导图像的梯度差距不要过大，则最终滤波窗口的损失函数为：
$$E(a_k,b_k)=\sum _{i\in w_k}((a_k{I}_i+b_k-p_i{)}^2+ϵa_k^2)$$通过最小二乘求解可得到：
$$a_k=\frac{\frac{1}{|w|}{\sum }_{i\in w_k}{I}_i{p}_i-{\mu }_k{\bar{p}}_k}{{\sigma }_k^2+ϵ}$$$$b_k={\bar{p}}_k-a_k{\mu }_k$$其中，${\mu }_k$是引导图像$I$在窗口$w_k$中的平均值，${\sigma }_k$是引导图像$I$在窗口$w_k$中的方差，$|w|$是窗口$w_k$中像素的数量，${\bar{p}}_k$是待滤波图像$p$在窗口$w_k$中的均值。在计算每个窗口的线性系数时，可以发现一个像素会被多个窗口包含，也就是说，每个像素都由多个线性函数所描述。因此，如之前所说，要具体求某一点的输出值时，只需将所有包含该点的线性函数值平均即可，如下：
$$q_i=\frac{1}{|w|}\sum _{k:i\in w_k}(a_k{I}_i+b_k)={\bar{a}}_i{I}_i+{\bar{b}}_i$$此处，$w_k$是所有包含像素$i$的窗口，$k$是其中心位置。最后得到的算法为：

其中的$f_{mean}$是指具有窗口半径$r$的均值滤波。在图像去雾中使用原图像的灰度图作为引导图像，使用所计算出的透射率图作为导向滤波的原始图像，即实现对透射率的细化，其Matlab实现如下：

function q = guidedfilter(I, p, r, eps)
%% 导向滤波
% 输入参数I为引导图像，在图像去雾中使用原图像的灰度图作为引导图像
% 输入参数p为原始图像，在图像去雾中使用透射率图作为原始图像
% 输入参数r为滤波半径
% 输入参数eps为正则化参数
[hei, wid] = size(I);
N = boxfilter(ones(hei, wid), r); 

mean_I = boxfilter(I, r) ./ N;
mean_p = boxfilter(p, r) ./ N;
mean_II = boxfilter(I.*I, r) ./ N;
mean_Ip = boxfilter(I.*p, r) ./ N;
% this is the covariance of (I, p) in each local patch.
var_I = mean_II - mean_I .* mean_I;
cov_Ip = mean_Ip - mean_I .* mean_p; 

a = cov_Ip ./ (var_I + eps); 
b = mean_p - a .* mean_I; 

mean_a = boxfilter(a, r) ./ N;
mean_b = boxfilter(b, r) ./ N;

q = mean_a .* I + mean_b; 
end

其中函数boxfilter为均值滤波函数，其Matlab程序如下：

function imDst = boxfilter(imSrc, r)
%% 均值滤波函数
% 输入参数imSrc为原始窗口，输入参数r为均值滤波半径
[hei, wid] = size(imSrc);
imDst = zeros(size(imSrc));

%cumulative sum over Y axis
imCum = cumsum(imSrc, 1);
%difference over Y axis
imDst(1:r+1, :) = imCum(1+r:2*r+1, :);
imDst(r+2:hei-r, :) = imCum(2*r+2:hei, :) - imCum(1:hei-2*r-1, :);
imDst(hei-r+1:hei, :) = repmat(imCum(hei, :), [r, 1]) - imCum(hei-2*r:hei-r-1, :);

%cumulative sum over X axis
imCum = cumsum(imDst, 2);
%difference over Y axis
imDst(:, 1:r+1) = imCum(:, 1+r:2*r+1);
imDst(:, r+2:wid-r) = imCum(:, 2*r+2:wid) - imCum(:, 1:wid-2*r-1);
imDst(:, wid-r+1:wid) = repmat(imCum(:, wid), [1, r]) - imCum(:, wid-2*r:wid-r-1);
end

可以看出，在自实现的均值滤波函数中，没有对求得数值进行归一化，因此在导向滤波中对于mean_I等变量的求解皆除了N，即进行了归一化。对于均值滤波，也可以使用Matlab中自带的imboxfit函数进行，但其在图像边缘处的处理不如自实现的boxfilter好。
那么，使用导向滤波对所求得的透射率进行细化（事实上，双边滤波也可以实现细化，因为双边滤波也具有边缘保留，但其需要经过调参才能获得较好的去雾结果），一般设均值滤波半径为求解暗通道时使用的最小值滤波半径的4~8倍。其主函数为：

clc;
clear; 

%% -----------图像去雾算法----------------
% 加载图片
img = imread('testImages\test1.png');
figure;imshow(img)

% 暗通道图
win_dark = getdarkimg(double(img) / 255);

% 基于导向滤波的去雾图像
De_Gf_img = anyuanseGF(img, win_dark);
figure;imshow(De_Gf_img);

其余函数皆在上文中给出，笔者制作了一个简单的gui，以实现修改导向滤波半径和正则化系数时，去雾结果差异的直观展示，下面展示几个实现效果较好的去雾例子：




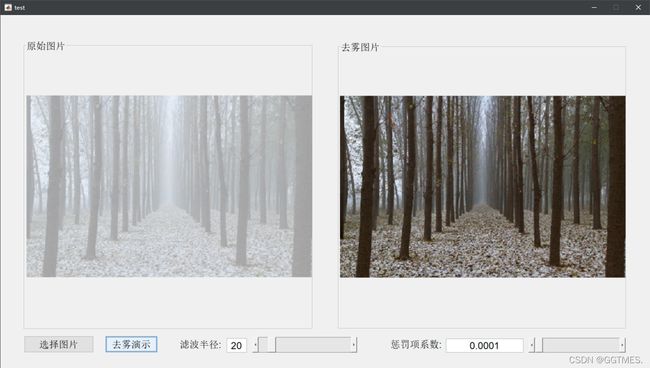
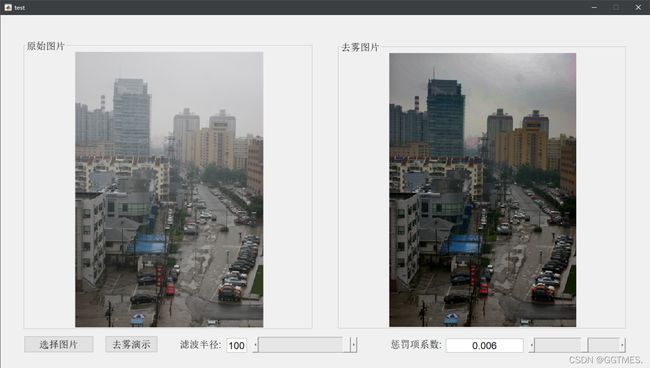
通过上述实际运用可以看出，在普遍情况下，对于利用导向滤波进行去雾的效果还是很明显的并且耗费的时间是很短的，基本可以实现实时求解。但同时，通过上述最后两个示例可以看出，利用导向滤波进行图像去雾时，在大面积留白区域的效果并不是很好，这是便需要进行对于导向滤波细化透射率的调参，最终才可以得到一个不那么奇怪的结果。但是，对于普遍的含雾图像而言已经可以取得较好的结果。