线性判别分析(LDA)二分类的原理及python实现
问题引入
已知一个样本存在两个属性,根据属性的不同可以分为三个类别,现需要依据下面的训练集,给出某样本的属性值判断该样本属于下面的哪一个类别。
| 属性1 | 属性2 | 类别 |
|---|---|---|
| 4 | 2 | 1 |
| 2 | 4 | 1 |
| 2 | 3 | 1 |
| 3 | 6 | 1 |
| 4 | 4 | 1 |
| 9 | 10 | 0 |
| 6 | 8 | 0 |
| 9 | 5 | 0 |
| 8 | 7 | 0 |
| 10 | 8 | 0 |
符号说明
n n n表示列属性的个数。
x i \textbf{x}_i xi为nx1的列向量,在表格中代表一个不包括类别属性的行。
c = 0 , 1 , ⋯ , k , ⋯ c={0,1,\cdots,k,\cdots} c=0,1,⋯,k,⋯表示类别的集合,对应上述表格中的0、1。
m k m^k mk表示类别为c的样本总个数。
X k \textbf{X}^k Xk表示类别k组成的矩阵,大小为 m k × n m^k\times{n} mk×n。
x i k , k ∈ c \textbf{x}_i^k,k\in{c} xik,k∈c为nx1列向量,在表格中表示类别为k的属性行。
m = ∑ k ∈ c m k m=\sum_{k\in{c}}{m^k} m=∑k∈cmk表示所有样本数。
θ \theta θ表示位于直线 l l l上的nx1的单位列向量。
基本思想
之前我们讲过logistic回归进行分类,现在我们要以一种新的方式LDA进行分类,LDA常常用于二分类问题以及多分类的降维处理,本篇文章先讲解关于二分类的问题。
由于两类数据过于繁多,导致无法直接对数据属于哪一类进行判断,LDA的基本思想是对于两类数据,想办法将两类数据映射到一条合适的直线上,此时只需要找到直线上一个可以将两类数据分开到两边的点,就可以直观且简便地判断某个样本数据属于哪一类了。
但并不是所有直线都可以找到这个分界点,如下图所示,紫色与红色分别代表两类数据,左侧将两类数据的一部分映射到一起了显然增加了判断难度,右侧可以找到一个蓝色的点将两类数据区分开来,相对于左侧图像而言,右侧映射到直线的数据,具有类内尽可能聚集,不同类数据尽可能分散的特点,如何利用数学公式去描述这种特点,就是Linear Discriminant Analysis(LDA)的任务了。
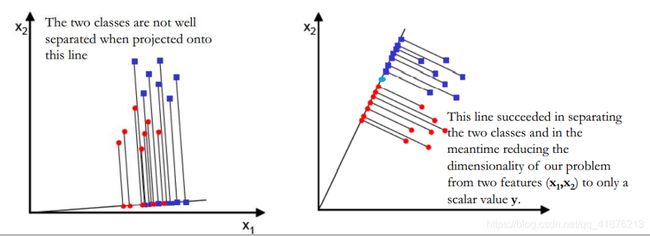
推导过程
首先需要理解映射的概念,具体内容在PCA降维的投影部分中讲解过,简单来说,若单位向量 θ \theta θ是直线 l l l上的单位向量,那么样本数据 x i \textbf{x}_i xi在直线 l l l上的投影距离为 θ T x i \theta^T\textbf{x}_i θTxi。
类别k的样本平均向量为
u k = 1 m k ∑ i = 1 m k x i , k ∈ c (1) \textbf{u}^{k}=\frac{1}{m^k}\sum_{i=1}^{m^k}\textbf{x}_i,k\in{c}\tag{1} uk=mk1i=1∑mkxi,k∈c(1)
基本思想中说类内距离尽可能小,描述类内距离的方式千千万,让所有样本向量向平均向量聚集却不失为一种好的策略,那么类别k中的样本向量 x i k \textbf{x}_i^k xik在映射到直线 l l l之后,与平均向量之间的距离(注意该距离不是欧式距离)可以表示为
∑ i = 1 m k ( θ T x i k − θ T u k ) 2 \sum_{i=1}^{m^k}(\theta^T\textbf{x}_i^k-\theta{^T}\textbf{u}^k)^2 i=1∑mk(θTxik−θTuk)2
所有类别的距离和为
∑ k ∈ c ∑ i = 1 m k ( θ T x i k − θ T u k ) 2 \sum_{k\in{c}}\sum_{i=1}^{m^k}(\theta^T\textbf{x}_i^k-\theta{^T}\textbf{u}^k)^2 k∈c∑i=1∑mk(θTxik−θTuk)2
这就表示我们在基本思想中提到过的类内距离和。
全局最小并不代表每一类中都是最小的,即便存在某条直线 l 1 l1 l1,使其中某一类的类内距离比在 l l l中还要小,但是求全局最小也不失为一种比较好的策略。
将该公式改写成下面的形式
∑ k ∈ c ∑ i = 1 m k ( θ T x i k − θ T u k ) 2 = ∑ k ∈ c ∑ i = 1 m k [ θ T ( x i k − u k ) ] [ θ T ( x i k − u k ) ] = ∑ k ∈ c ∑ i = 1 m k [ θ T ( x i k − u k ) ] [ ( x i k − u k ) T θ ] = ∑ k ∈ c ∑ i = 1 m k θ T ( x i k − u k ) ( x i k − u k ) T θ = θ T [ ∑ k ∈ c ∑ i = 1 m k ( x i k − u k ) ( x i k − u k ) T ] θ = θ T S w θ \begin{matrix} \begin{aligned} &\sum_{k\in{c}}\sum_{i=1}^{m^k}(\theta^T\textbf{x}_i^k-\theta{^T}\textbf{u}^k)^2\\ =&\sum_{k\in{c}}\sum_{i=1}^{m^k}[\theta^T(\textbf{x}_i^k-\textbf{u}^k)][\theta^T(\textbf{x}_i^k-\textbf{u}^k)]\\ =&\sum_{k\in{c}}\sum_{i=1}^{m^k}[\theta^T(\textbf{x}_i^k-\textbf{u}^k)][(\textbf{x}_i^k-\textbf{u}^k)^T\theta]\\ =&\sum_{k\in{c}}\sum_{i=1}^{m^k}\theta^T(\textbf{x}_i^k-\textbf{u}^k)(\textbf{x}_i^k-\textbf{u}^k)^T\theta\\ =&\theta^T[\sum_{k\in{c}}\sum_{i=1}^{m^k}(\textbf{x}_i^k-\textbf{u}^k)(\textbf{x}_i^k-\textbf{u}^k)^T]\theta\\ =&\theta^T\textbf{S}_w\theta \end{aligned} \end{matrix} =====k∈c∑i=1∑mk(θTxik−θTuk)2k∈c∑i=1∑mk[θT(xik−uk)][θT(xik−uk)]k∈c∑i=1∑mk[θT(xik−uk)][(xik−uk)Tθ]k∈c∑i=1∑mkθT(xik−uk)(xik−uk)TθθT[k∈c∑i=1∑mk(xik−uk)(xik−uk)T]θθTSwθ
数学感觉较好的网友肯定可以意识到, S w \textbf{S}_w Sw(w表示within class)就是所有类别的散度矩阵和了,本人虽然没有拜读过先人们的论文,但能隐约地感觉到散度矩阵就是像这样慢慢地抽象并产生其数学意义的。
我们已经了解到类内距离了,接下来开始表述类间距离。
对于二分类问题,类间距离可以定义为两类平均向量之间的距离,如下。
( θ T u 0 − θ T u 1 ) 2 = θ T ( u 0 − u 1 ) ( u 0 − u 1 ) T θ = θ T S b θ (2) \begin{matrix} \begin{aligned} &(\theta^T\textbf{u}^0-\theta^T\textbf{u}^1)^2\\ =&\theta^T(\textbf{u}^0-\textbf{u}^1)(\textbf{u}^0-\textbf{u}^1)^T\theta\\ =&\theta^T\textbf{S}_b\theta \end{aligned} \end{matrix}\tag2 ==(θTu0−θTu1)2θT(u0−u1)(u0−u1)TθθTSbθ(2)
与 S w \textbf{S}_w Sw相似, S b \textbf{S}_b Sb(b表示between class)表示类间的散度矩阵。
在基本思想中我们提到,需要使类间距离最大,类内距离最小,我们的求解目标变为
arg max θ θ T S b θ θ T S w θ (3) \arg\max_{\theta}\frac{\theta^T\textbf{S}_b\theta}{\theta^T\textbf{S}_w\theta}\tag3 argθmaxθTSwθθTSbθ(3)
即存在分子又存在分母,利用求导的方式求导求极值比较复杂,分母求最小值,总会存在一个最小值t使 θ T S w θ = t \theta^T\textbf{S}_w\theta=t θTSwθ=t,t为一个常数,一般我们默认求极小值,分子部分可以加个负号,变为 − θ T S b θ -\theta^T\textbf{S}_b\theta −θTSbθ,此时求解目标变为
arg min θ − θ T S b θ θ T S w θ = t (4) \begin{matrix} \arg \min_{\theta}-\theta^T\textbf{S}_b\theta\\ \theta^T\textbf{S}_w\theta=t \end{matrix}\tag4 argminθ−θTSbθθTSwθ=t(4)
教材中的求解方式都是以分数形式(3)求解的,个人认为直接列出公式(4)求解也并无不妥,此时就可以利用拉格朗日求极值。
J ( θ ) = − θ T S b θ + λ ( θ T S w θ − t ) J(\theta)=-\theta^T\textbf{S}_b\theta+\lambda(\theta^T\textbf{S}_w\theta-t) J(θ)=−θTSbθ+λ(θTSwθ−t)
求导数,令其为0。
d J ( θ ) d θ = − 2 S b θ + λ 2 S w θ = 0 \frac{dJ(\theta)}{d\theta}=-2\textbf{S}_b\theta+\lambda{2\textbf{S}_w\theta=0} dθdJ(θ)=−2Sbθ+λ2Swθ=0
⟺ \iff ⟺
S b θ = λ S w θ (5) \textbf{S}_b\theta=\lambda\textbf{S}_{w}\theta\tag{5} Sbθ=λSwθ(5)
由(2)知
S b θ = ( u 0 − u 1 ) ( u 0 − u 1 ) T θ \textbf{S}_b\theta=(\textbf{u}^0-\textbf{u}^1)(\textbf{u}^0-\textbf{u}^1)^T\theta Sbθ=(u0−u1)(u0−u1)Tθ
由于 ( u 0 − u 1 ) T θ (\textbf{u}^0-\textbf{u}^1)^T\theta (u0−u1)Tθ是一个常量,不妨令 λ θ = ( u 0 − u 1 ) T θ \lambda_\theta=(\textbf{u}^0-\textbf{u}^1)^T\theta λθ=(u0−u1)Tθ
那么
S b θ = ( u 0 − u 1 ) λ θ = λ S w θ \textbf{S}_b\theta=(\textbf{u}^0-\textbf{u}^1)\lambda_\theta=\lambda\textbf{S}_{w}\theta Sbθ=(u0−u1)λθ=λSwθ
最终可以求得
θ = S w − 1 ( u 0 − u 1 ) λ θ λ \theta=\textbf{S}_w^{-1}(\textbf{u}^0-\textbf{u}^1)\frac{\lambda_\theta}{\lambda} θ=Sw−1(u0−u1)λλθ
由于 θ \theta θ是与直线 l l l同向的向量,所以常数项可以省略,最终目标解 θ ∗ \theta^{*} θ∗为
θ ∗ = S w − 1 ( u 0 − u 1 ) (6) \theta^{*}=\textbf{S}_w^{-1}(\textbf{u}^0-\textbf{u}^1)\tag6 θ∗=Sw−1(u0−u1)(6)
同时,这一结论也表明LDA在二分类中,只能求得一类平行的向量。
计算步骤以及python代码
1.计算平均值 u k u^k uk
2.计算散度矩阵 S w \textbf{S}_w Sw
3.计算逆 S w − 1 \textbf{S}_w^{-1} Sw−1
4.计算 θ ∗ = t e x t b f S w − 1 ( u 0 − u 1 ) \theta^*=textbf{S}_w^{-1}(\textbf{u}^0-\textbf{u}^1) θ∗=textbfSw−1(u0−u1)
5.计算样本在直线上的位置 θ T x i \theta^T\textbf{x}_i θTxi
将上述问题计算之后,并绘图

计算结果

python代码
import matplotlib.pyplot as plt
import numpy as np
def draw1(data,theta,num,colors):
x=[[] for i in range(2)]
for ele in data:
x[ele[-1]].append(ele[:-1])
#绘制原始数据
for i in range(num):
x[i]=np.array(x[i])
plt.scatter(x[i][:,0],x[i][:,1],color=colors[i])
#绘制被的映射直线
plt.plot([0,theta[0]*15],[0,theta[1]*15])
#绘制映射到直线上的点
for i in range(num):
for ele in x[i]:
ta=theta*np.dot(ele,theta)
plt.plot([ele[0],ta[0]],[ele[1],ta[1]],color=colors[i],linestyle="--")
plt.scatter(ta[0],ta[1],color=colors[i])
plt.show()
def c2(data,num):
n=data.shape[1]-1
#存储x值
x=[[] for i in range(num)]
#存储u值
u=[[]for i in range(num)]
#存储Sw
sw=np.zeros([n,n])
for ele in data:
x[ele[-1]].append(ele[:-1])
for i in range(num):
x[i]=np.array(x[i])
u[i]=np.mean(x[i],axis=0)
print("1计算平均值:\n",u)
for i in range(num):
x[i]=x[i]-u[i]
sw=sw+np.dot(x[i].T,x[i])
print("2x_i去中心化:\n",x)
print("3计算散度矩阵S_w:\n",sw)
#计算theta
theta=np.dot(np.linalg.inv(sw),(u[0]-u[1]).T)
#单位化
fm=0
for i in range(n):
fm=fm+theta[i]**2
return theta/np.sqrt(fm)
data=np.array([[4,2,1],[2,4,1],[2,3,1],[3,6,1],[4,4,1],[9,10,0],[6,8,0],[9,5,0],[8,7,0],[10,8,0]])
colors=['red','green']
theta=c2(data,2)
print("4计算直线向量theta:\n",theta)
draw1(data,theta,2,colors)