Andrew Ng吴恩达深度学习Course_2笔记
术语概念
NLP::自然语言处理
CV(computer vision):计算机视觉
超参数:
正则化:
Mini-batch:子训练集,面对训练集样本过多的情况,梯度下降迭代一次时间过长,因此分为多个子集
RMSprop:root meam square prop,加速梯度下降
第一周 深度学习的实用层面
训练/验证/测试集
过去:验证集和测试集的比例常用7 : 3,如果没有明确设置验证集,也可以用60%训练、20%验证和20%测试集来划分
现在:数据达到百万级别,所需验证/测试集数量的比例大大降低,训练集占比可达99%以上
最好确保验证集和测试集的数据来自同一分布
如果不需要无偏评估,则可以不需要独立的测试集(验证集中包含)
偏差和方差
衡量训练集和验证集的错误率,偏差反映拟合程度,方差反映量化能力
训练集错误率高,偏差大;训练集和验证集之间的错误率差值高,方差大

L2正则化
正则化通常有助于避免过拟合或减少网络误差
如今越来越倾向使用L2 regularization模型,因为L1所占存储空间更大
L2正则化简单理解就是为了泛化特征,使网络不要太依赖某些太明显的特征
常用λ(lambda)来表示正则化
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) + λ 2 m ∣ ∣ w ∣ ∣ 2 J(w,b)=\frac1m\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})+\frac{\lambda}{2m}||w||^2 J(w,b)=m1i=1∑mL(y^(i),y(i))+2mλ∣∣w∣∣2
在python中避免保留字段冲突,我们用lambd代替lambda来表示正则化参数
下图有误,应是w:(n[l],n[l-1]),n[l-1]表示隐藏单元的数量,n[l]表示l层单元的数量
∣ ∣ ⋅ ∣ ∣ F 2 ||·||^2_F ∣∣⋅∣∣F2表示frobenius范数,即矩阵L2范数(但一般不说是L2),表示一个矩阵中所有元素的平方和
∣ ∣ w [ l ] ∣ ∣ F 2 = ∑ i = 1 n [ l ] ∑ j = 1 n [ l − 1 ] ( w i j [ l ] ) 2 ||w^{[l]}||^2_F=\sum_{i=1}^{n^{[l]}}\sum_{j=1}^{n^{[l-1]}}(w^{[l]}_{ij})^2 ∣∣w[l]∣∣F2=i=1∑n[l]j=1∑n[l−1](wij[l])2
紫字:在原本梯度下降公式上新增的正则化,重新定义dw
d w [ l ] = ( f r o m b a c k p r o p ) + λ m w [ l ] → w [ l ] = w [ l ] − α d w [ l ] dw^{[l]}=(from\quad backprop)+\frac{\lambda}mw^{[l]}\\ \to w^{[l]}=w^{[l]}-\alpha dw^{[l]} dw[l]=(frombackprop)+mλw[l]→w[l]=w[l]−αdw[l]
绿字:解释原理,相当于给矩阵w乘以了 ( 1 − α λ m ) (1-\frac{\alpha\lambda}m) (1−mαλ) 倍的权重,因此L2正则化也被称为“权重衰减”,λ越大,w越小
正则化之所以能减少过拟合,是因为减小了部分权重w,即减弱了隐藏单元对全局的影响。以tanh()举例,w越小,z越小,z的取值范围越接近线性
Dropout正则化
随机失活几个隐藏节点,精简每个样本训练所需神经网络
Inverted dropout反向随机失活
举例:在一个l=3的神经网络中,d3构造一个随机的只有0和1的矩阵,a3是原矩阵,然后对应元素相乘,0的位置的节点会被消除。keep-prob=0.8,意味着d3的元素有0.8的概率为1,即有20%的节点被失活。每一层的keep-drop可以不一样。
核心思想:此算法随机去掉一部分节点,就相当于L2正则化的变线简化,只不过这个算法是去除掉了。但是最后训练时通过除以keep-prob保证结果期望值不变,做到了简化+保持概率正则化。
测试阶段不会执行dropout
dropout预防过拟合
通过随机消除节点,可以防止前后层节点产生依赖,使权重趋于分散(平均),不会使某个节点的权重远大于其他的权重,防止随着学习过程加深导致过拟合。
dropout被作为一种正则化的代替形式,类似于L2正则化
其他正则化方法
数据增广
early stopping
归一化输入
将数据化为标准分布, μ \mu μ和 σ 2 \sigma^2 σ2都是由训练集数据计算来的
如果输入特征处于不同范围,将特征值归一化( μ \mu μ=0, σ 2 \sigma^2 σ2=1),可以帮助学习算法运行得更快
梯度消失和梯度爆炸
梯度消失:当w略小于1的时候,激活函数将指数式递减
梯度爆炸:当w略大于1的时候,激活函数将爆炸式增长
为了解决梯度消失和梯度爆炸的问题,要谨慎选择初始化参数,随机产生的数据要满足标准分布(让一部分略大于1,一部分略小于1)
w[L]=np.random.randn(shape)*np.sqrt(2/n[l-1])
让每一层输出的方差降低因权重而受到的影响,避免权重矩阵随着层数越深而越来越大或者越来越小
梯度逼近和梯度检验
梯度逼近
双边逼近求导,非直接求导(拉格朗日?)
f ( θ + ε ) − f ( θ − ε ) 2 ε ≈ g ( θ ) f ′ ( θ ) = lim ε → 0 f ( θ + ε ) − f ( θ − ε ) 2 ε \frac{f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon}\approx g(\theta)\\ f'(\theta)=\lim_{\varepsilon\rightarrow0}\frac{f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon} 2εf(θ+ε)−f(θ−ε)≈g(θ)f′(θ)=ε→0lim2εf(θ+ε)−f(θ−ε)

梯度检验
check:
∣ ∣ d θ a p p r o x − d θ ∣ ∣ 2 ∣ ∣ d θ a p p r o x ∣ ∣ 2 + ∣ ∣ d θ ∣ ∣ 2 \frac{||d\theta_{approx}-d\theta ||_2}{||d\theta_{approx}||_2+||d\theta ||_2} ∣∣dθapprox∣∣2+∣∣dθ∣∣2∣∣dθapprox−dθ∣∣2
三角验证,分母表示三角形两条边长度之和,分子表示第三条长度,这样比值总是落在[0 ,1]之间
如果检验值很小,则说明代码计算的梯度和另外检验的梯度很接近
注意事项:
- 只在debug中使用检验,训练过程不用
- 如果算法的梯度检验失败,要检查所有项来找出bug
- 记得使用正则化
- 梯度检验不能和dropout一起使用
第二周 优化算法
Mini-batch梯度下降法
mini-batch一步梯度下降法原理如下,假设训练集有500万个样本,取m=1000的mini-batch(共5000个mini-batch)。使用batch,遍历一代只能做一次梯度下降,而使用mini-batch,一代能做5000个梯度下降
mini-batch的成本函数会产生振荡,是因为每次训练用的集不一样,可能会有一些噪音数据,如x{1} 和 x{2}的训练难度不同
紫字:当mini-batch size=1时,每个样本都是一个单独的mini-batch,被称为随机梯度下降法
绿字:一般mini-batch大小取值在(1,m)之间
- 如果mini-batch大小为1,则会失去mini-batch示例中矢量化带来的的好处。
- 如果mini-batch的大小是m,那么你会得到批量梯度下降,这需要在进行训练之前对整个训练集进行处理。
注意事项:
-
当batch大小在2000以下时,建议直接使用batch
-
一般mini-batch大小取64,128,256,512(符合CPU/GPU内存)
-
mini-batch的大小为一个重要的变量,需要多尝试几个不同的值,找到能够最有效地减少成本函数的那个
步骤
我们要使用mini-batch要经过两个步骤:
-
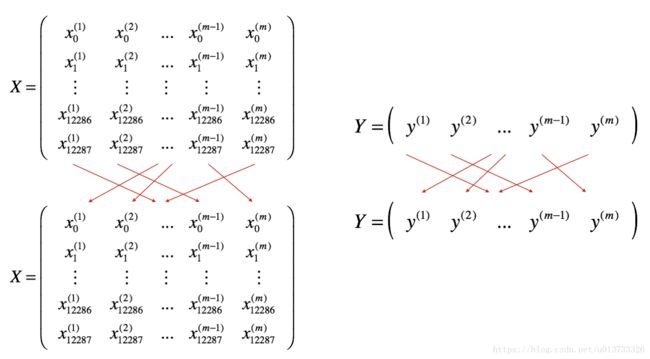
把训练集打乱,但是X和Y依旧是一一对应的,之后,X的第i列是与Y中的第i个标签对应的样本。乱序步骤确保将样本被随机分成不同的小批次。如下图,X和Y的每一列代表一个样本
-
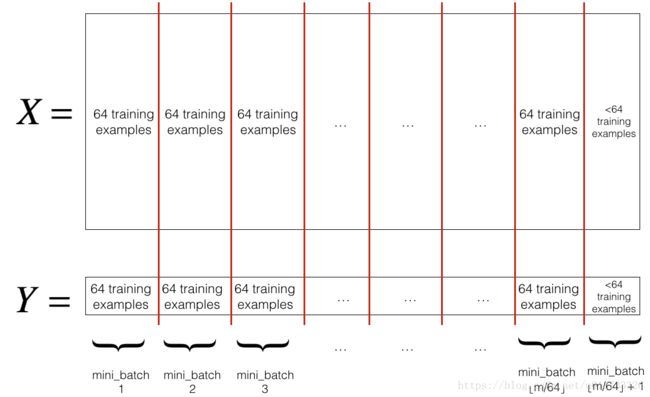
切分,我们把训练集打乱之后,我们就可以对它进行切分了。这里切分的大小是64,如下图:
指数加权平均
以伦敦气温为例
V t = β V t − 1 + ( 1 − β ) θ t V_t=βV_{t-1}+(1-β)θ_t Vt=βVt−1+(1−β)θt
不断调整平均数,β大小决定曲线波动 ,增加β会使红线稍微向右移动,减少β会在红线内产生更多的振荡。
0.910 约等于0.35,即10天影响力下降近三分之一
偏差修正
当β=0.98时,因为v0=0,v1=0.02 * θ1,远小于当天温度θ1,前几天的偏差较大
因此 V t V_t Vt可修正为 V t 1 − β t \frac{V_t}{1-\beta^t} 1−βtVt,结果从紫线变绿线
动量梯度下降法
计算梯度的指数加权平均数,并利用该梯度更新权重,减缓梯度下降的幅度。
V d w = β V d w + ( 1 − β ) d w V d b = β V d b + ( 1 − β ) d b → w = w − α V d w , b = b − α V d b V_{dw}=\beta V_{dw}+(1-\beta)dw\\ V_{db}=\beta V_{db}+(1-\beta)db\\ \to w=w-\alpha V_{dw}, \quad b=b-\alpha V_{db} Vdw=βVdw+(1−β)dwVdb=βVdb+(1−β)db→w=w−αVdw,b=b−αVdb
纵轴方向运动变小,横轴方向运动变快。
紫字:本质上能够最小化碗装函数,想象dw、db等微分项给了从山上滚下来的雪球一个加速度,动量momentum项相当于速度,β始终小于1,相当于摩擦阻力,使得球不会无限加速下去。
RMSprop
用斜率控制波动,把波动曲线当成wb的二维函数,消除摆动
S d w = β S d w + ( 1 − β ) ( d w ) 2 S d b = β S d b + ( 1 − β ) ( d b ) 2 → w = w − α d w S d w , b = b − α d b S d b S_{dw}=\beta S_{dw}+(1-\beta)(dw)^2\\ S_{db}=\beta S_{db}+(1-\beta)(db)^2\\ \to w=w-\alpha \frac{dw}{\sqrt{S_{dw}}}, \quad b=b-\alpha \frac{db}{\sqrt{S_{db}}} Sdw=βSdw+(1−β)(dw)2Sdb=βSdb+(1−β)(db)2→w=w−αSdwdw,b=b−αSdbdb
和上一个动量momentum不一样的是,这里是梯度平方的加权平均。上一个没有平方,把梯度看作向量,因此在振荡方向上的db会被抵消,降低了震荡;这里把梯度当作标量,平方之后开方,因此梯度值较大的db会被削减较多,降低了震荡。
两种方法目的相同,都是为了消除梯度下降中的震荡,同时允许使用一个更大的学习率加快算法学习速度。
紫字:实际运算过程会加一个 ε = 1 0 − 8 \varepsilon=10^{-8} ε=10−8,防止出现 S d w S_{dw} Sdw过小,导致出现 d w S d w \frac{dw}{\sqrt{S_{dw}}} Sdwdw 过大的情况
Adam优化算法
相当于动量momentum和RMSprop结合
V d w c o r r e c t = V d w 1 − β 1 t , V d b c o r r e c t = V d b 1 − β 1 t S d w c o r r e c t = S d w 1 − β 2 t , S d b c o r r e c t = S d b 1 − β 2 t w = w − α V d w c o r r e c t S d w c o r r e c t + ε , b = b − α V d b c o r r e c t S d b c o r r e c t + ε V_{dw}^{correct}=\frac{V_{dw}}{1-\beta_1^t},\quad V_{db}^{correct}=\frac{V_{db}}{1-\beta_1^t}\\ S_{dw}^{correct}=\frac{S_{dw}}{1-\beta_2^t},\quad S_{db}^{correct}=\frac{S_{db}}{1-\beta_2^t}\\ w=w-\alpha \frac{V_{dw}^{correct}}{\sqrt{S_{dw}^{correct}}+\varepsilon},\quad b=b-\alpha \frac{V_{db}^{correct}}{\sqrt{S_{db}^{correct}}+\varepsilon} Vdwcorrect=1−β1tVdw,Vdbcorrect=1−β1tVdbSdwcorrect=1−β2tSdw,Sdbcorrect=1−β2tSdbw=w−αSdwcorrect+εVdwcorrect,b=b−αSdbcorrect+εVdbcorrect

总结:具有动量的梯度下降通常可以有很好的效果,但由于小的学习速率和简单的数据集所以它的影响几乎是轻微的。另一方面,Adam明显优于小批量梯度下降和具有动量的梯度下降,如果在这个简单的模型上运行更多时间的数据集,这三种方法都会产生非常好的结果,然而,我们已经看到Adam收敛得更快。
Adam的一些优点包括相对较低的内存要求(虽然比梯度下降和动量下降更高)和通常运作良好,即使对参数进行微调(除了学习率α αα)
学习率衰减
绿色:学习率α在后期减小,可以使得曲线在最小值附近的一小块区域内摆动,而非大幅度摆动
第三周 超参数调试、batch正则化与程序框架
调试处理
需调试的超参数:
α >
β(β1、β2) = hidden units隐藏单元 = mini-batch size >
layers隐藏层数 = learning rate decay学习率衰减
常用方法:将超参设为坐标轴,随机取点,而不是网格搜索,因为你不知道哪些超参数比其他的更重要
举一个很极端的例子,就比如在Adam算法中防止除零操作的ε的值,一般为1的负8次方,但是和学习率α相比,ε就显得不那么重要了
为超参数选取合适的范围
有些超参数(如学习率α)非常敏感,变化0.001就会有很大的差别,如果采用均匀分布取值,对调参是不利的,所以会采用如下的对数形式
α = 1 0 r \alpha = 10^r α=10r,对r均匀分布取值
β也是一个非常重要的超参数,越靠近1,变化的影响越大,因此1-β后同样采用对数形式,这样越靠近1,取值的间隔就越小,远离1的取值间隔变大
超参数训练的实践:Pandas VS Caviar
只照顾一个模型(使用熊猫策略)还是一起训练大量的模型(鱼子酱策略)在很大程度上取决于在你能力范围内,你能够拥有多大的计算能力(就是高性能电脑和低性能电脑的区别)
batch norm归一化
batch归一化的适用不仅是输入层,还适用于深度隐藏层
正则化网络的激活函数
先进行标准归一化处理定位,然后让机器自动学习合适的归一化参数(γ,β)重缩放
μ = 1 m ∑ i z ( i ) σ 2 = 1 m ∑ i ( z ( i ) − μ ) 2 z n o r m ( i ) = z ( i ) − μ σ 2 + ε z ^ ( i ) = γ z n o r m ( i ) + β \mu = \frac1m\sum_iz^{(i)}\\ \sigma^2=\frac1m\sum_i(z^{(i)}-\mu)^2\\ z^{(i)}_{norm}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\varepsilon}} \\\hat{z}^{(i)}=\gamma z^{(i)}_{norm}+\beta μ=m1i∑z(i)σ2=m1i∑(z(i)−μ)2znorm(i)=σ2+εz(i)−μz^(i)=γznorm(i)+β

注意:归一化里的β和优化算法里的β不是同一个参数
实践中,batch归一化通常和训练集的mini-batch一起使用
参数b是一个恒定的常数,会被均值消减法抵消,因此在batch归一化中不考虑,也可视作被归纳进β学习
这里的平均值是横向的,不同的z向量上同一位置神经元的平均值,这些在Z矩阵中处于同一行上的值自然用同一b值,所以b平均=b
batch norm的作用
因为参数w,b的作用,每一层的输出和输入分布都不太一样,对于特别多层的网络,比如Google的动不动上百层,后面的累积分布差异跟原数据分布完全不一样,然后每换一个batch,分布又可能往另一种方式差异化,形象点,对于后面的layer来说,每次学的东西可能都天差地别,不知道自己在干啥。
batch norm(归一化)使得每一层的值围绕固定的均值和方差变动,稳定了每层的输入值,增强了每层的独立性,有助于加速整个网络的学习
可以把batch norm和dropout一起使用,得到更强大的正则化效果,而使用较大的mini-batch大小可以减少正则化效果
但是不要把batch归一化当作正则化,把它当作归一化隐藏单元激活值并加速学习的方式,正则化只是副作用
测试时的batch norm
将mini-batch中计算好的 μ , σ 2 \mu,\sigma^2 μ,σ2放到测试集中测试要逐个处理,不能整体算平均,要使用指数加权平均值来估计mini-batch的情况
softmax回归模型
logstic回归的一般形式,能实现多样化分类,最终的输出为一个向量,表示概率,元素总和为1
无隐藏层的情况下,任何两个分类之间的决策边界都是线性的
本质还是二分法
softmax的损失函数
L ( y ^ , y ) = − ∑ j = 1 C y i l o g y j ^ L(\hat{y},y)=-\sum_{j=1}^Cy_ilog\hat{y_j} L(y^,y)=−j=1∑Cyilogyj^
极大似然估计法
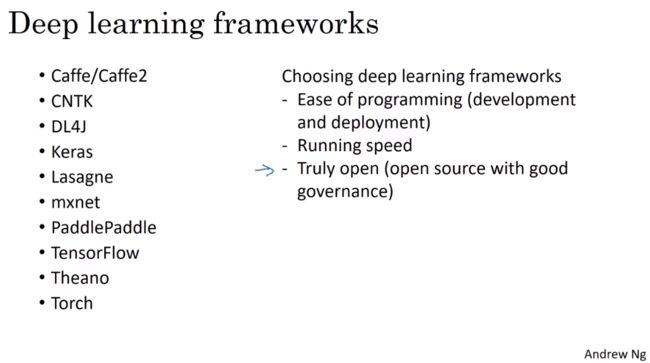
深度学习框架
通过编程框架,可以使用比低级语言(如Python)更少的代码来编写深度学习算法。即使一个项目目前是开源的,项目的良好管理有助于确保它即使在长期内仍然保持开放,而不是仅仅为了一个公司而关闭或修改。
详细情况网上查阅