国科大模式识别导论作业3:神经网络
目录
- 题目
- 代码
-
- data.py
- utils.py
- network.py
- main.py
- 结果
整理一下近期作业中的编程题,仅供交流学习
题目
本题使用的数据如下:
第一类 10 个样本(三维空间):
[ 1.58, 2.32, -5.8], [ 0.67, 1.58, -4.78], [ 1.04, 1.01, -3.63],
[-1.49, 2.18, -3.39], [-0.41, 1.21, -4.73], [1.39, 3.16, 2.87],
[ 1.20, 1.40, -1.89], [-0.92, 1.44, -3,22], [ 0.45, 1.33, -4.38],
[-0.76, 0.84, -1.96]
第二类 10 个样本(三维空间):
[ 0.21, 0.03, -2.21], [ 0.37, 0.28, -1.8], [ 0.18, 1.22, 0.16],
[-0.24, 0.93, -1.01], [-1.18, 0.39, -0.39], [0.74, 0.96, -1.16],
[-0.38, 1.94, -0.48], [0.02, 0.72, -0.17], [ 0.44, 1.31, -0.14],
[ 0.46, 1.49, 0.68]
第三类 10 个样本(三维空间):
[-1.54, 1.17, 0.64], [5.41, 3.45, -1.33], [ 1.55, 0.99, 2.69],
[1.86, 3.19, 1.51], [1.68, 1.79, -0.87], [3.51, -0.22, -1.39],
[1.40, -0.44, -0.92], [0.44, 0.83, 1.97], [ 0.25, 0.68, -0.99],
[ 0.66, -0.45, 0.08]
- 请编写两个通用的三层前向神经网络反向传播算法程序,一个采用批量方式更新权
重,另一个采用单样本方式更新权重。其中,隐含层结点的激励函数采用双曲正切
函数,输出层的激励函数采用 sigmoid 函数。目标函数采用平方误差准则函数。 - 请利用上面的数据验证你写的程序,分析如下几点:
(a) 隐含层不同结点数目对训练精度的影响;
(b) 观察不同的梯度更新步长对训练的影响,并给出一些描述或解释;
(c) 在网络结构固定的情况下,绘制出目标函数值随着迭代步数增加的变化曲线
代码
以下文件在同一目录下
data.py
# 存储处理好的数据
import numpy as np
from numpy import ones, zeros_like
# 每类取7个作为训练数据,3个作为测试数据
x1 = np.array([[1.58, 2.32, -5.8], [0.67, 1.58, -4.78], [1.04, 1.01, -3.63], [-1.49, 2.18, -3.39], [-0.41, 1.21, -4.73],
[1.39, 3.16, 2.87], [1.20, 1.40, -1.89], [-0.92, 1.44, -3.22], [0.45, 1.33, -4.38],
[-0.76, 0.84, -1.96]], dtype=float).reshape(-1, 3)
y1 = np.zeros_like(x1)
y1[:, 0] = ones([len(y1)], dtype=float)
x1 = np.hstack((x1, y1))
ext = np.ones(len(x1))
ext = ext.reshape(10, -1)
x1 = np.hstack((ext, x1))
x2 = np.array([[0.21, 0.03, -2.21], [0.37, 0.28, -1.8], [0.18, 1.22, 0.16], [-0.24, 0.93, -1.01], [-1.18, 0.39, -0.39],
[0.74, 0.96, -1.16], [-0.38, 1.94, -0.48], [0.02, 0.72, -0.17], [0.44, 1.31, -0.14],
[0.46, 1.49, 0.68]]).reshape(-1, 3)
y2 = zeros_like(x2)
y2[:, 1] = ones([len(y2)], dtype=float)
x2 = np.hstack((ext, x2, y2))
x3 = np.array([[-1.54, 1.17, 0.64], [5.41, 3.45, -1.33], [1.55, 0.99, 2.69],
[1.86, 3.19, 1.51], [1.68, 1.79, -0.87], [3.51, -0.22, -1.39],
[1.40, -0.44, -0.92], [0.44, 0.83, 1.97], [0.25, 0.68, -0.99],
[0.66, -0.45, 0.08]]).reshape(-1, 3)
y3 = zeros_like(x3)
y3[:, 2] = ones([len(y3)], dtype=float)
x3 = np.hstack((ext, x3, y3))
train_data = np.vstack((x1[:7], x2[:7], x3[:7]))
test_data = np.vstack((x1[7:], x2[7:], x3[7:]))
utils.py
# 记录需要用到的公式
from numpy import exp, ones_like
import math
# 双曲正切函数
def tan_h(x):
return math.tanh(x)
def diff_tang_h(x):
return 1.0 / (1 + pow(x, 2))
# sigmoid
def sigmoid(x):
return 1.0 / (1 + exp(-x))
# sigmoid 求导
def diff_sigmoid(x):
out = sigmoid(x)
return out * (1 - out)
# 线性函数
def linear(x):
return x
# 线性函数求导
def diff_linear(x):
return ones_like(x) # 对线性函数求导 结果全是1
network.py
# 定义神经网络
from numpy import dot, zeros, random, multiply
import matplotlib.pyplot as plt
from data import *
from utils import *
class Network:
# 参数列表:输入层、隐藏层、输出层的节点数
def __init__(self, input_layer_num, hidden_layer_num, output_layer_num):
self.input_layer_num = input_layer_num
self.hidden_layer_num = hidden_layer_num
self.output_layer_num = output_layer_num
self.data_i = ones(self.input_layer_num)
self.data_net_hidden = ones(self.hidden_layer_num)
self.data_net_output = ones(self.output_layer_num)
self.data_y = ones(self.hidden_layer_num)
self.data_z = ones(self.output_layer_num)
self.f0_net_k = ones(self.output_layer_num)
self.delta_k = ones(self.output_layer_num)
# 初始化权重
self.wi = random.random((self.hidden_layer_num, self.input_layer_num))
self.wo = random.random((self.hidden_layer_num, self.output_layer_num))
self.delta_wi_temp = self.wi
self.delta_wo_temp = self.wo
# 正向计算过程
def forward(self, input):
self.data_i = input
self.data_net_hidden = dot(self.wi, self.data_i) # nxd x dx1 -- nx1
self.data_y = np.array(list(map(tan_h, self.data_net_hidden)))
self.data_net_output = dot(self.data_y, self.wo) # 1xn nxc
self.data_z = list(map(sigmoid, self.data_net_output))
return self.data_z
# 反向传播
def BP(self, target, updata_flag, rate_1, rate_2):
loss_t_k = target - self.data_z
for i in range(self.output_layer_num):
self.f0_net_k[i] = diff_sigmoid(self.data_net_output[i])
self.delta_k = np.multiply(self.f0_net_k, loss_t_k)
data_y_temp = self.data_y.reshape(-1, 1)
delta_wo = dot(data_y_temp, self.delta_k.reshape(1, 3))
epsilon = zeros(self.hidden_layer_num).reshape(-1, 1)
for i in range(self.hidden_layer_num):
epsilon[i] = multiply(self.delta_k, self.wo[i:i + 1][0]).sum()
delta_wi = rate_2 * dot(epsilon, self.data_i.reshape(1, -1))
self.delta_wo_temp = self.delta_wo_temp + delta_wo
self.delta_wi_temp = self.delta_wi_temp + delta_wi
if updata_flag == 1:
self.wo = self.wo + rate_2 * delta_wo
self.wi = self.wi + rate_1 * delta_wi
loss = 0.5 * dot((target - self.data_z), (target - self.data_z).reshape(-1, 1))
return loss
def train(self, patterns, input_data, rate_1, rate_2):
loss_set = []
acc_set = []
step = 0
sample_len = len(patterns)
sample_num = 0
rate_temp = 0
for m in range(5000):
step += 1
updata_flag = 1
for p in patterns:
sample_num += 1
inputs = p[1:4].reshape(-1, 1)
targets = p[4:]
if sample_num == sample_len:
updata_flag = 1
self.forward(inputs)
loss = self.BP(targets, updata_flag, rate_1, rate_2)
rate = self.test(input_data)
rate_temp = rate_temp + rate
# 每100步输出一次当前状态
if step % 100 == 0:
loss_set.append(loss)
print("loss:", loss, "acc:", rate)
if step % 10 == 0:
rate_temp = rate_temp / 10
acc_set.append(rate_temp)
rate_temp = 0
return loss_set, acc_set
def test(self, input_data):
correct_num = 1
for p in input_data:
inputs = p[1:4].reshape(-1, 1)
targets = p[4:]
output = self.forward(inputs)
out_class = np.where(output == np.max(output))
if targets[out_class] == 1:
correct_num = correct_num + 1
rate = correct_num / len(input_data)
return rate
def plot_plot(self, loss_set0, loss_set1, loss_set2):
set_len = len(loss_set1)
plt.plot(range(set_len), loss_set0, range(set_len), loss_set1, range(set_len), loss_set2)
plt.legend(['rate=0.001', 'rate=0.005', 'rate=0.1'])
# plt.title('learning_rate:'+name_num)
plt.show()
main.py
此处为了多画不同的图,需要调整Network()括号内的参数并运行
from network import *
if __name__ == '__main__':
rate_1 = 0.001
rate_2 = 0.005
rate_3 = 0.1
# 输入层 隐藏层 输出层
network1 = Network(3, 6, 3)
loss_set0, acc0 = network1.train(train_data, test_data, rate_1, rate_1)
network2 = Network(3, 6, 3)
loss_set1, acc1 = network2.train(train_data, test_data, rate_2, rate_2)
network3 = Network(3, 6, 3)
loss_set2, acc2 = network2.train(train_data, test_data, rate_3, rate_3)
network3.plot_plot(loss_set0, loss_set1, loss_set2)
结果
通过调整学习率与隐藏层节点数量,运行编写得到的main.py(如附录),可以得到以下三幅图像:
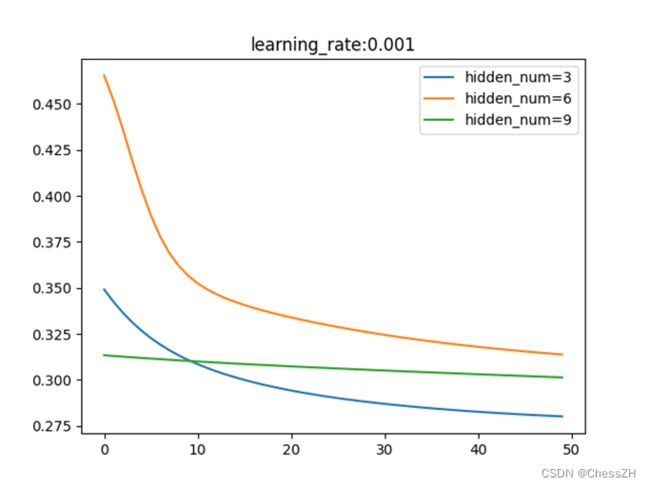

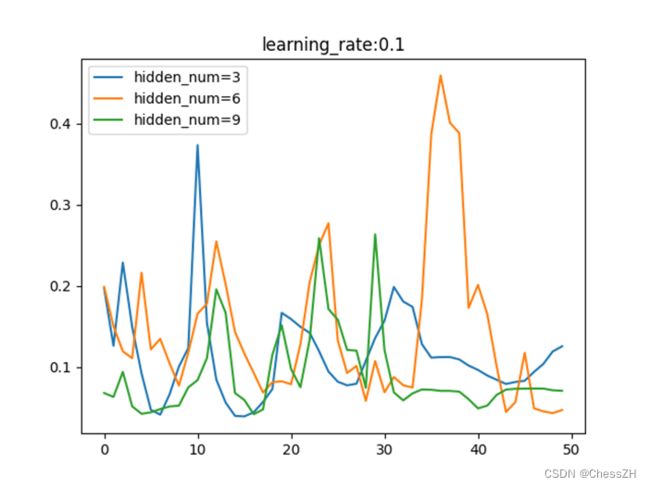
通过分析以上图像,我们可以简单归纳以下结论:
1) 在一定范围内,隐藏层结点个数越多,虽然网络复杂度提升了,但是训练精度也提高了;
2) 在一定范围内,梯度更新步长会使目标函数值收敛速度加快,但是一旦步长过大,会变得难以收敛;
3) 同一种结构的目标函数值变化曲线如下图所示。
