一文搞定有穷状态自动机(FA)——DFA、NFA区别、转换以及DFA化简
有穷状态自动机(Finite Automata, FA)分为确定的和不确定的,简称为DFA和NFA。
确定有穷自动机(DFA)
不确定的有穷自动机(NFA)
形式定义:
DFA与NFA的区别
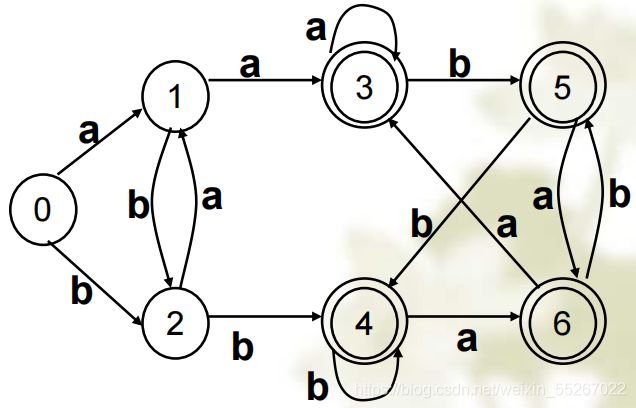
DFA与NFA的区别在于,NFA的状态转换过程中可以有空串,如下图即为NFA。

这就导致了一个问题:开始之后,在给出字符a或b之前,我们能够确定当前是处于1状态还是2状态吗?很显然,我们是无法确定的,因此才被称为不确定的有穷自动机,因为空串的存在,我们无法确定当前的具体状态是什么。
所以NFA的不确定表现我们可以概括为:
- 多值映射
- 带空转移
因此在很多时候,我们都需要将NFA转换为DFA。
NFA转换为DFA
理论准备:
定义1的意思便是,在当前状态下,我们首先将当前状态以及经过空串能够到达的状态放到一起组成一个闭包。
定义2的意思便是,将该闭包中的每个状态,都加上一个确定的输入,如外界输入一个a,从而进入到新的状态,再将这些新的状态以及这些新的状态加上空串能够到达的状态放到一起组成一个新的闭包。
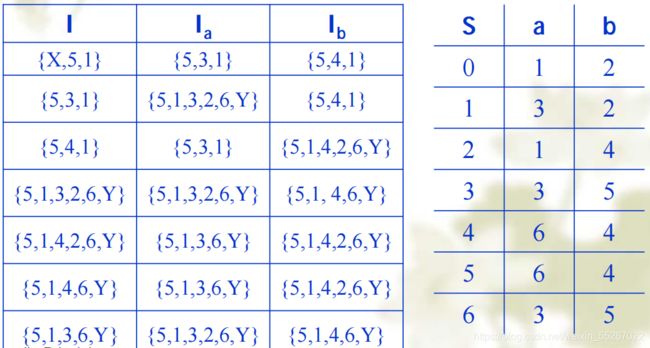
则经过确定化可以得到如下表格:

以第一行为例,一开始的起始状态为X,经过空串能够到达的状态有5和1,因此第一个闭包为{X, 5, 1},然后输入一个a,则X输入a,没有任何新的状态,5输入a还是5,1输入a进入到3,又因为5经过空串可以到达1,因此输入一个a得到的新的闭包为{5, 3, 1},同理可得输入一个b得到的新的闭包。然后后面再将得到的新的闭包作为一个状态,根据输入a或b又得到新的闭包,以此往复,直至再没有新的闭包产生为止。
经过确定化处理之后,我们可以发现,已经没有空串了,每个状态都是确定的。
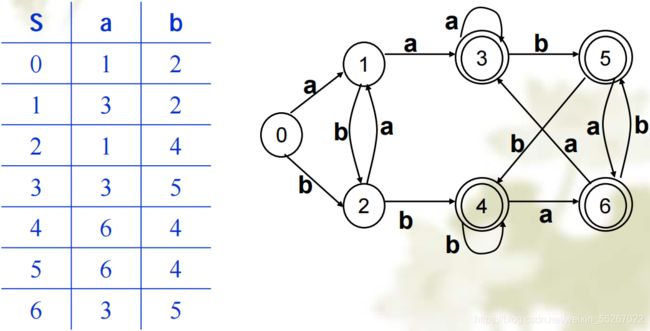
到这里,转换过程便是结束了,可以发现的是,对于原来的正规式,转换成NFA之后,我们还是能够马上看出其要表达的意思,但是转换成DFA之后,整个问题就变的很抽象了,完全就不知道其对应的正规式是什么了,因此这也是DFA的一个缺点吧。
DFA的化简
等价状态:若分别从状态 s 和 t 出发而停于终态能读出同一个串α,则称s, t 为等价状态;反之则称为可区别状态。
其中,终态与非终态一定是可区别的。
则首先状态集S={0, 1, 2, 3, 4, 5, 6}可以分为S1={0, 1, 2}和S2={3, 4, 5, 6}
那么对于S1,0,1,2是可区别的吗?
由于0状态下输入a进入状态1,输入b进入状态2;1状态输入a进入终态3,输入b进入状态2;2状态输入a进入状态1,输入b进入终态4。
可以发现,0,1,2状态进入终态的路径集合都不相同,因此相互之间都是可区别的。
对于S2,由于3,4,5,6状态输入a,b都能够直接进入到终态,即进入终态的路径集合都是一样的,因此是等价状态。
综上所述,S最终可以被分割为(0)S11={0},(1)S12={1},(2)S13={2}以及(3)S2={3, 4, 5, 6},DFA简化为: