手把手教做无人驾驶算法(二十六)--基于终端约束的MPC 控制
关于MPC终端约束问题,其实就是稳定性与可行性的分析,欢迎感兴趣的一起交流探讨,如有错误,还请指正,不胜感激。
基于终端约束的MPC控制,理论部分可以参考资料:
【Linear MPC入门】Model Predictive Control Algorithm, Feasibility and Stability - 知乎
这里,终端约束数据可以用数据驱动来代替,这样就可以把MPC与数据驱动相结合起来,但是好处不仅仅是为了与数据驱动联合,终端约束有什么好处呢?上面的参考资料也给出了参考。
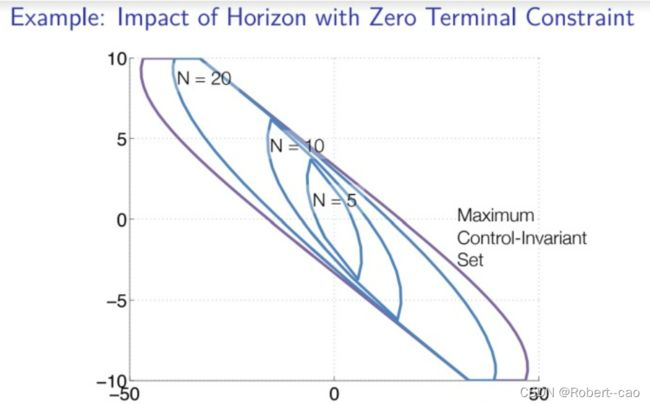
对于一般MPC而言,相当于零点为终点,不过,使用Zero Terminal Constraint是非常苛刻的,导致可行域减少了很多。同时,MPC的预测的步数N越少,可行域也越少。
对于可行域使用凸多面体表示,如上图:
function [ invariantGoalSet ] = computeInvariantGoalSet( A, B, Q, R )
[K,~,~] = dlqr(A,B,Q,R);
Acl = A-B*K;
w_max = 0.05;
W = Polyhedron([w_max w_max; w_max -w_max; -w_max -w_max; -w_max w_max]);
X{1} = zeros(size(Acl,1),1); % Initialize the set
for i = 1:10000
Set = Acl*X{i} + W; % Propagate the uncertanty
Set.minHRep() % Compute minimal representation
Set.minVRep() % Compute minimal representation
X{i+1} = Set;
% Check if the algorithm has covnerged
if i > 1
if (X{i+1}.contains(X{i})) && (X{i}.contains(X{i+1}))
invariantGoalSet = X{i+1}; % Set invaraint to the current iterate
disp(['Invariant set computed in i = ',num2str(i),' iterations'])
break
end
end
end
end下面给出一个例子:
这里,首先使用MPC去解除有效的解,即状态值,输入值,同时使用这些量可以计算出状态量,形成安全集,使用这些安全集SS作为终端约束以及代价约束,核心部分代码如下:
def addTrajectory(self, x, u):
# Add the feasible trajectory x and the associated input sequence u to the safe set
self.SS.append(copy.copy(x))
self.uSS.append(copy.copy(u))
# Compute and store the cost associated with the feasible trajectory
cost = self.computeCost(x, u)
self.Qfun.append(cost)
# Initialize zVector
self.zt = np.array(x[self.ftocp.N])
# Augment iteration counter and print the cost of the trajectories stored in the safe set
self.it = self.it + 1
print("Trajectory added to the Safe Set. Current Iteration: ", self.it)
print("Performance stored trajectories: \n", [self.Qfun[i][0] for i in range(0, self.it)])
def computeCost(self, x, u):
# Compute the cost in a DP like strategy: start from the last point x[len(x)-1] and move backwards
for i in range(0,len(x)):
idx = len(x)-1 - i
if i == 0:
cost = [np.dot(np.dot(x[idx],self.Q),x[idx])]
else:
cost.append(np.dot(np.dot(x[idx],self.Q),x[idx]) + np.dot(np.dot(u[idx],self.R),u[idx]) + cost[-1])
# Finally flip the cost to have correct order
return np.flip(cost).tolist()上面为计算SS安全集以及代价值
# Terminal Constraint if SS not empty --> enforce the terminal constraint
if SS is not None:
constr += [SS * lambVar[:,0] == x[:,self.N], # Terminal state \in ConvHull(SS)
np.ones((1, SS.shape[1])) * lambVar[:,0] == 1, # Multiplies \lambda sum to 1
lambVar >= 0] # Multiplier are positive definite
# Cost Function
cost = 0
for i in range(0, self.N):
# Running cost h(x,u) = x^TQx + u^TRu
#ost += quad_form(x[:,i], self.Q) + norm(self.R**0.5*u[:,i])**2
# cost += quad_form(x[:,i], self.Q) + quad_form(u[:,i], self.R)
cost += norm(self.Q**0.5*x[:,i])**2 + norm(self.R**0.5*u[:,i])**2
# Terminal cost if SS not empty
if SS is not None:
cost += Qfun[0,:] * lambVar[:,0] # It terminal cost is given by interpolation using \lambda
else:
cost += norm(self.Q**0.5*x[:,self.N])**2 # If SS is not given terminal cost is quadratic
这里代码是终端约束以及终端代价约束。
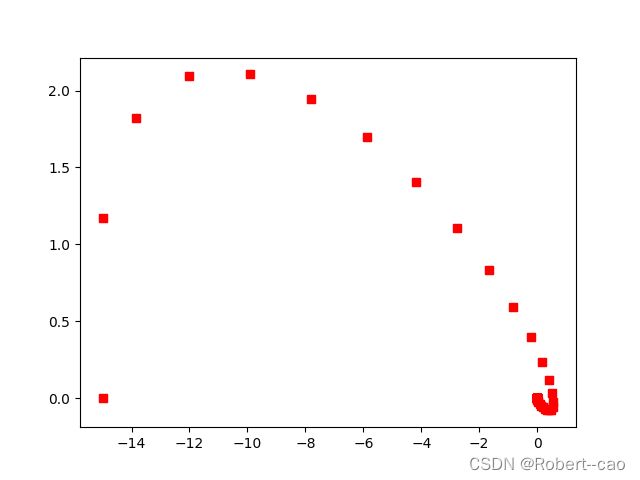
没有终端约束的轨迹:
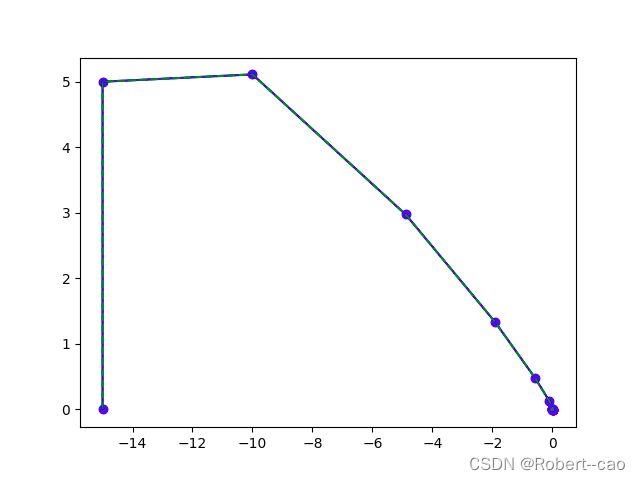
带有终端约束的轨迹:
具体代码地址,这个代码为python 写的:
MPC/LinearLMPC at main · caokaifa/MPC · GitHub