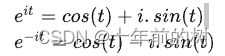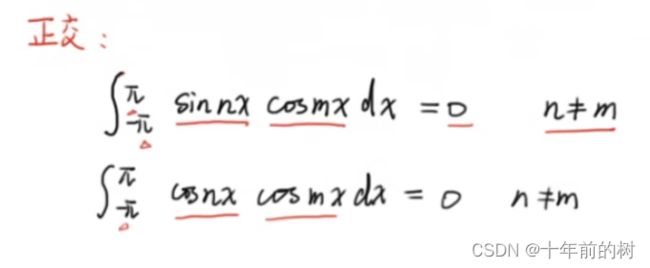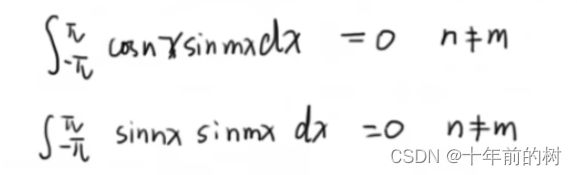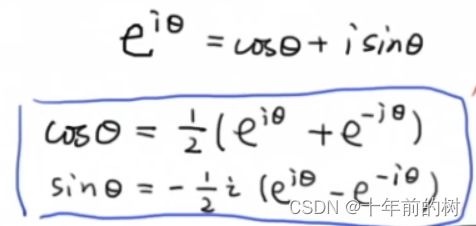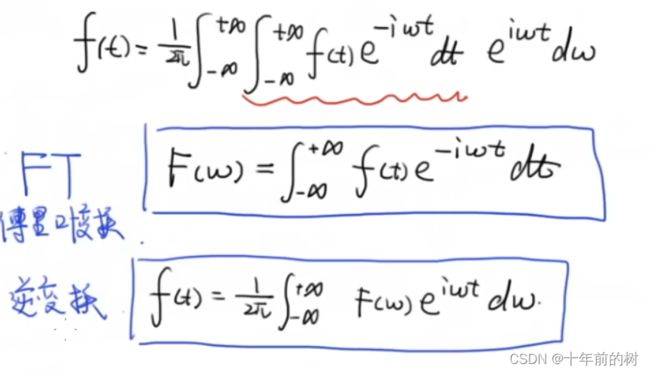傅里叶变换
目录
零、参考文献
一、时域和频域的概念
1、时域(时间域)
2、频域(频率域)
二、相位谱
0)前言
1)相位谱引入
2)完整立体图
三、傅里叶变换
0)前言
1)引入
2)欧拉公式
(1)虚数 i 的理解
(2)欧拉公式的作用
3)指数形式的傅里叶变换
4)理论总结
四、数学推导
1)三角函数的正交性
(1)三角函数系的概念编辑
(2)正交性是什么
编辑
2)周期为2Π的函数展开为傅里叶级数
3)周期为2L(T)的函数展开为傅里叶级数
4)傅里叶级数的复数形式简化表达式
5)从傅里叶级数推导傅里叶变换
6)应用
零、参考文献
【官方双语】形象展示傅里叶变换_哔哩哔哩_bilibili
傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎
纯干货数学推导_傅里叶级数与傅里叶变换_Part1_三角函数的正交性_哔哩哔哩_bilibili
【官方双语】形象展示傅里叶变换_哔哩哔哩_bilibili
图形计算器
一、时域和频域的概念
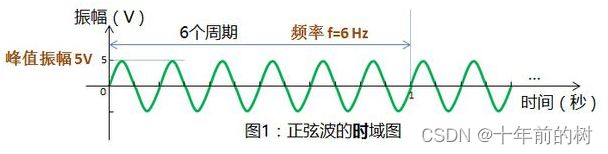
1、时域(时间域)
自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x(t)是描述信号在不同时刻取值的函数。
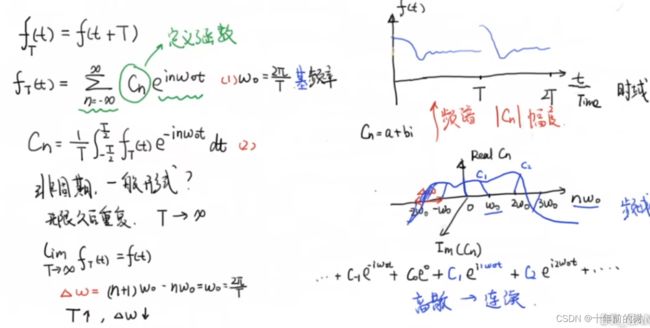
2、频域(频率域)
自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。
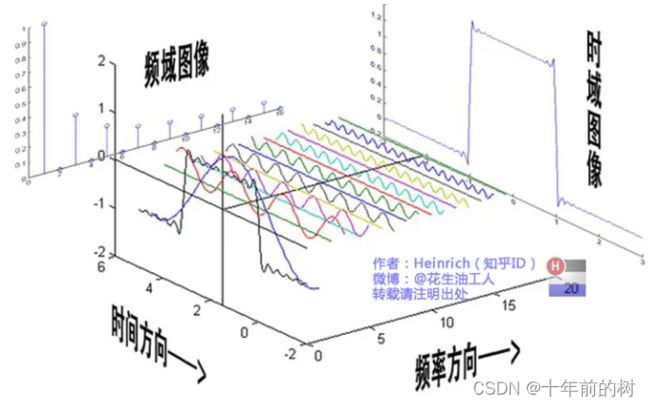
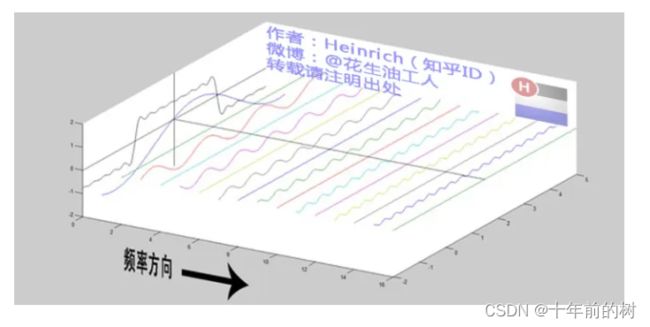
下面的图片更清楚:(从侧面的角度去看)
每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为0的正弦波,也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。cos(0t)就是一个周期无限长的正弦波,也就是一条直线,所以在频域,0频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
二、相位谱
0)前言
很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
1)相位谱引入
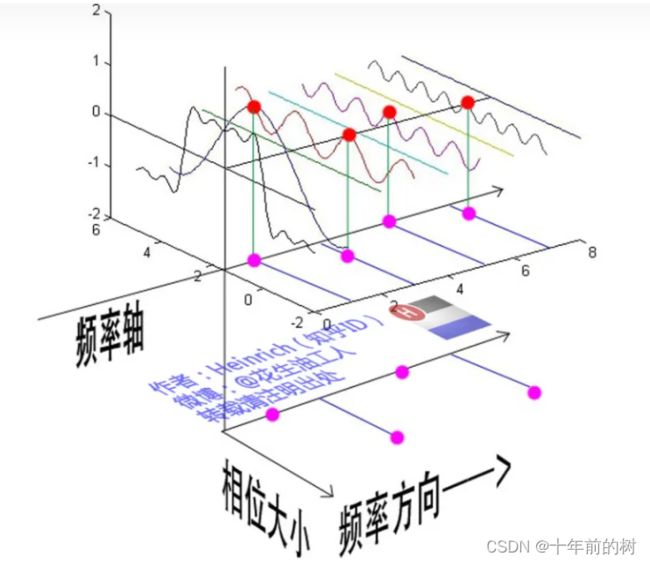
通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。
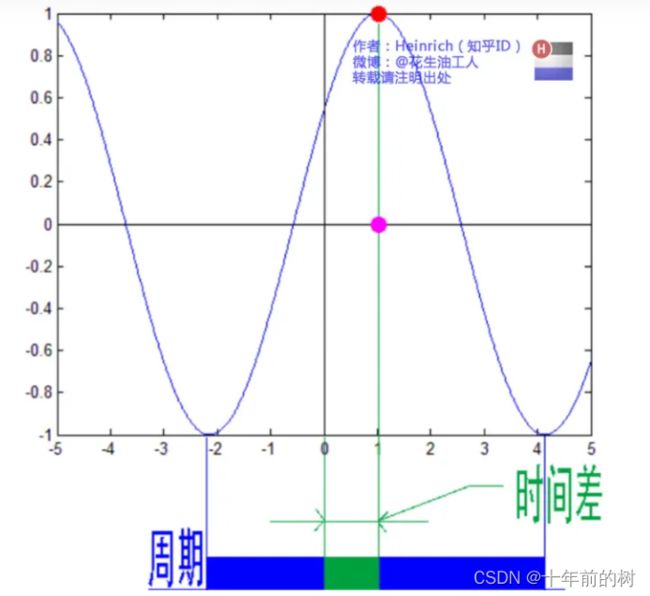
鉴于正弦波是周期的,我们需要设定一个用来标记正弦波位置的东西。在图中就是那些小红点。小红点是距离频率轴最近的波峰,而这个波峰所处的位置离频率轴有多远呢?为了看的更清楚,我们将红色的点投影到下平面,投影点我们用粉色点来表示。当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。
这里需要纠正一个概念:时间差并不是相位差。如果将全部周期看作2Pi或者360度的话,相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi,就得到了相位差。
2)完整立体图
相位谱的值域为(-pi,pi]
频谱是从侧面看,相位谱是从下面看
傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数
三、傅里叶变换
0)前言
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的
1)引入
傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。
而在我们接下去要讲的傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号,或者也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换
不过通过这样两幅图去比较,应该可以理解如何从离散谱变成了连续谱的了吧?原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。
2)欧拉公式
(1)虚数 i 的理解
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以3的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了180度。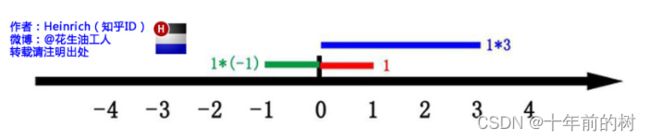
乘-1其实就是乘了两次 i 使线段旋转了180度,那么乘一次 i 呢——答案很简单——旋转了90度。同时,我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面,也称复平面。这样我们就了解到,乘虚数 i 的一个功能——旋转。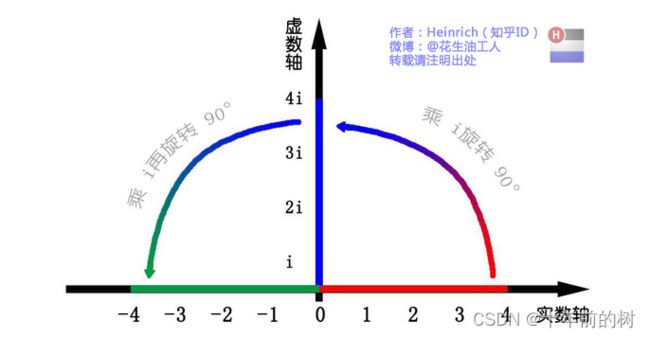
(2)欧拉公式的作用
这个公式关键的作用,是将正弦波统一成了简单的指数形式
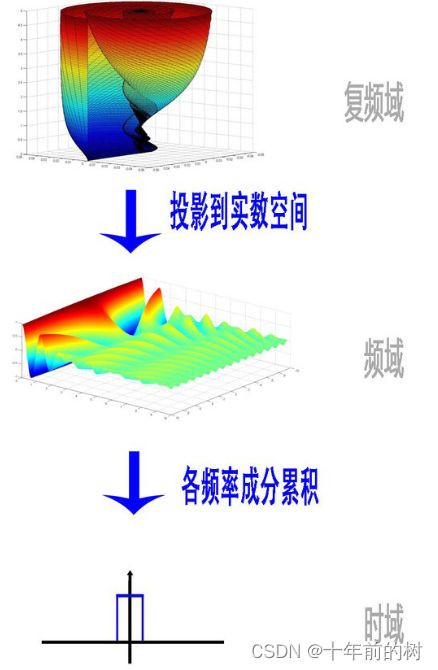
欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
3)指数形式的傅里叶变换
有了欧拉公式的帮助,我们便知道:正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。傅里叶变换出来的频谱不仅仅是可见光这样频率范围有限的叠加,而是频率从0到无穷所有频率的组合
这里,我们可以用两种方法来理解正弦波:
第一种前面已经讲过了,就是螺旋线在实轴的投影。
另一种需要借助欧拉公式的另一种形式去理解:
将以上两式相加再除2,得到:
这个式子可以怎么理解呢?
我们刚才讲过,e^(it)可以理解为一条逆时针旋转的螺旋线,那么e^(-it)则可以理解为一条顺时针旋转的螺旋线。而cos(t)则是这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了
4)理论总结
四、数学推导
1)三角函数的正交性
(1)三角函数系的概念
(2)正交性是什么
1.首先理解向量的正交,是当两个向量的夹角为90°时,它们的点积为0
2.将向量拓展到n维,点积表达式如下
3.如果a和b是一个函数,则点积表达式如下,如果在这个积分范围内等于0说明两个函数正交
4.对于三角函数而言,任取两个三角函数(m!= n)系在-pai到pai的积分为0
(证明可用积化和差公式)
对于第一个和第三个式子,n=m的时候也等于0
对于第二个和第四个式子,n=m的时候等于pai
2)周期为2Π的函数展开为傅里叶级数
利用正交性的性质
最终结果:
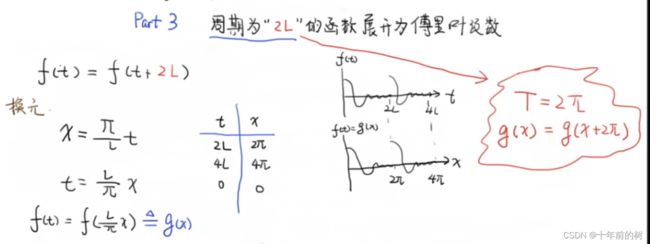
3)周期为2L(T)的函数展开为傅里叶级数
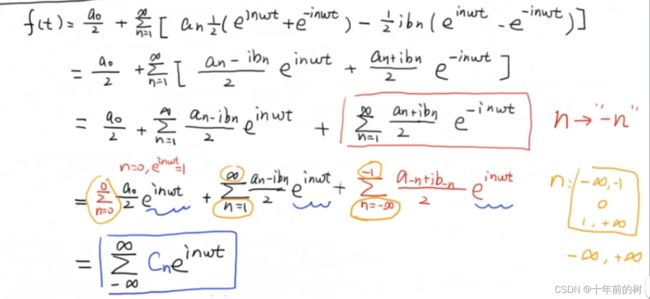
4)傅里叶级数的复数形式简化表达式
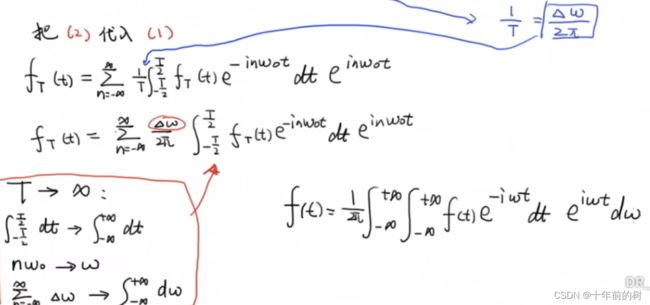
5)从傅里叶级数推导傅里叶变换
对于傅里叶变换公式的理解可以看3Blue1Brown的视频
(首先注意输出函数F(w)得到的是虚数)
一个旋转矢量做顺时针旋转,它的长度是时域信号在某一时间的大小,也可以理解为时域信号做w角频率(或者是f频率)的缠绕,做积分可以理解为,求在积分时间内,这个缠绕图形的质心的位置*积分时间(也就是时间越长,质心与原点距离越长),而F(w)则是记录这个质心的实部,也就是f频率下的幅值。
如果w的大小(其实w=2*pai*f)满足时域信号的分量的频率*2*pai,那么质心位置不动,经过积分就可得到质心的实部,也就是f频率下的幅值;对于其他不满足的,质心的位置会发生改变,经过积分虽可得到质心的实部,但是随着时间的增加,缠绕图像更可能在圆上均匀分开,积分会被削弱。
这也就使得频域图像振幅更加分散。
6)应用
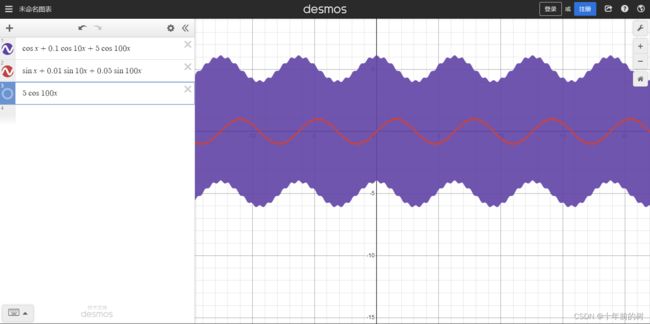
滤波处理
通过傅里叶变换得到频谱图,通过积分器滤除高频信号(一次积分或者二次积分)