深蓝学院-视觉SLAM课程-第2讲笔记--三维空间刚体运动

课程Github地址：https://github.com/wrk666/VSLAM-Course/tree/master

0. 内容

C++没有矩阵的运算，用别人的库来进行矩阵运算，其中Eigen库能够进行刚体运动的一些计算，由3部分构成：

• Core：矩阵的表达；
• Dense：稠密矩阵的计算，矩阵求逆，稠密矩阵的分解等；
• Geometry：旋转矩阵，欧拉角，四元数等。

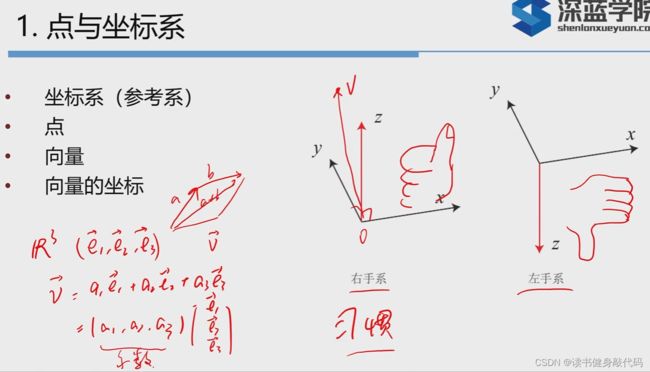
1. 点与坐标系

三维空间常用正交基来表示（常用右手系），一个向量是基底的线性组合，其系数就是这个向量在此空间的坐标

内积（点积）的结果是标量，
外积（叉积）的结果是向量

axb可以按行列式来写，也可以按照 a^ 来理解，写成a^b.若两向量平行，则叉积为0，此处的a^是一个反对称矩阵（罗德里格斯公式）

在SLAM中，坐标系有世界坐标系，机器人坐标系（不同传感器有各自的坐标系）

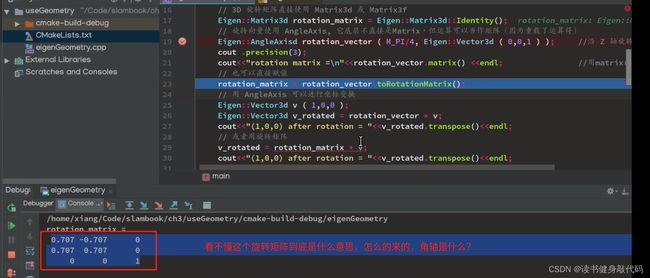
2. 旋转矩阵

R称为旋转矩阵：

• R是一个正交矩阵：$R^{-1}=R^T$, $R^{T}R=I$
• $det(R)=1$
  
  SO:Sepcial Orthogonal Group特殊正交群。

2->1的旋转：$a_1=R_{12}{a}_2$，其中$R_{12}$表示从2->1的旋转矩阵，从右读。（PPT上写错了）

$R$是[3,3]的向量，$t$是[3,1]的向量

为方便运算，构造向量
$$\tilde{a}=\left[\begin{array}{c}a\\ 1\end{array}\right]$$

则

$$\widetilde{a^{{}^{\prime }}}=\left[\begin{array}{c}{a}^{{}^{\prime }}\\ 1\end{array}\right]=\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\tilde{a}=T\tilde{a}$$
T叫变换矩阵。同理构造$\tilde{b}=T_1\tilde{a}$，$\tilde{c}=T_2\tilde{b}$，其中$T_1$，$T_2$在这里是[4,4]矩阵，可以进行运算，所以由a->c就可以简化表示为：
$$\tilde{c}=T_2{T}_1\tilde{a}$$

平移不是简单取反，还有旋转部分的逆的关系。（这里也算是个小坑，当时用四元数+平移来验证变换矩阵时踩了坑。）

齐次坐标乘以任意非零常数后仍然表达同一坐标。上面构造的转换矩阵$T$属于特殊欧式群$SE(3)$（下一讲介绍）

$$SE(3)=\left[\begin{array}{cc}{R}_{3\ast 3}& a_{3\ast 1}\\ 0^T& 1\end{array}\right]$$

3. 旋转向量和欧拉角

旋转向量的每个量都是一个角度和一个轴组成，旋转向量性质如下：

转换：
$\theta \ast n$(旋转向量)->旋转矩阵$R$：罗德里格斯公式
旋转矩阵$R$->$\theta \ast n$旋转矩阵转向量的公式（也可以使用对数映射，但是不常用）
$n$可以看作$R$的特征值为1的特征向量。

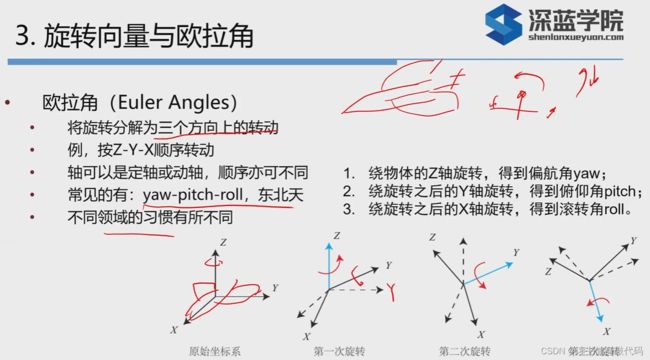
yaw-pitch-roll的定义有很多种（跟我之前做的陀螺仪加速度计的四元数姿态解算很密切），用之前要清楚到底是按照原来的轴转还是绕着旋转之后的轴转。

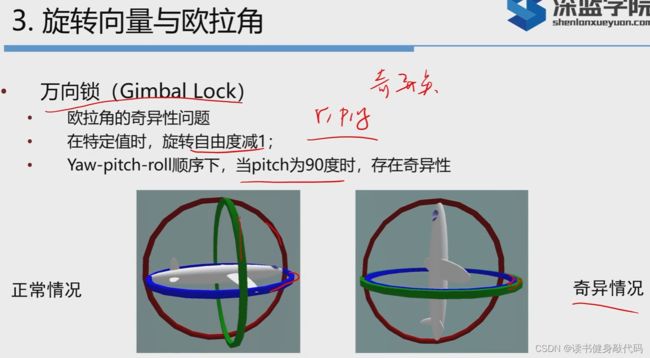
如上图，当pitch=90时，yaw和roll重叠了，只剩下两个自由度，这种情况叫做万向锁，可以证明，任何3自由量来描述3维旋转的情况都会碰到奇异点，任意一种欧拉角都会有奇异点，只是不同的定义方式下出现的情况不同。

4. 四元数（Quarterian）

由二维的单位复数扩展到3维的多个复数（3个虚部）
虚部的运算：和自己像复数，和别人算像叉积。

用实部和虚部部分组成一个向量来表示四元数

1. 上图中$q_a{q}_b$展开式的最后一行中应该是$+(s_a{z}_b+x_a{y}_b-x_b{y}_a+z_a{s}_b)k$。第三项错了。
   按照$[s_a{v}_a]$和$[s_b{v}_b]$的形式更好理解$q_a{q}_b$，标量乘向量不变，，再加上个向量的叉积（见第1节）
2. 定义共轭（虚部相反）
3. 定义四元数范数
4. 求逆，若是单位四元数，则其逆是其共轭
5. 数乘
6. element wise乘法

四元数乘法可以写成矩阵乘法，详见作业第5题：

接下来是四元数<->角轴

四元数如何使用呢？（如何表示一个空间点的旋转呢？）

用此三维点的坐标和0来构建一个虚四元数$p$，假设旋转后为$p^{{}^{\prime }}$，可以证明$p^{{}^{\prime }}$仍然是一个纯虚的四元数（到时候见作业）。实践中四元数用得较多，只用4个数，且没有歧义。

5. 实践–Eigen的初步使用

这里不太懂，等复习一下线性代数和矩阵论的知识后再来看看。