差分进化(DE)算法的Python实现

差分进化算法

差分进化算法(Differential Evolution Algorithm，DE)是一种高效的全局优化算法。它也是基于群体的启发式搜索算法，群中的每个个体对应一个解向量。

简单来说DE算法可用于求函数的极值点，例如：函数 的最小值点在，最小值为0。

差分进化算法对于不可导或者不连续也可以进行求解。

原理

这里只讲一下算法的思路，具体的细节可以在这里查看。

算法的主体分成4个步骤，下面以优化目标函数   求得最小值点为例：

1.初始化种群

这里需要确定的参数有：

种群大小，这表示种群中个体的个数，一般来说越大的值搜索到更优化的解的可能性更高，这里选取

每个个体（解）的维度，这是由目标函数决定的， 的输入有x1与x2两个参数，因此维度为2

以及解的搜索区间，这里限定，，即。

在给定搜索区间内随机生成5个可能的解，称为个体，假设他们分别是 (-0.3, 0.2), (0.1, 0.4), (0.9, -0.6), (-0.8, 0.4), (-0.1, 0.1)。这5个个体被称作种群。

2.产生变异个体

得到初始种群后，DE算法通过差分的方法生成变异个体。产生的方法是从种群中选择三个不同的个体a, b, c, 通过一下方式计算得到变异个体n：

其中F为缩放因子factor，它控制着变异程度。F越大，越不容易陷入局部极值点；F越小，越有利于收敛到局部极值点。对于例子中的目标函数，局部最小值点与全局最小值点重合，因此选择较小的F值得到的最终结果会更加精确。但是实际使用到DE算法进行优化的目标函数往往不满足这一特征，需要考虑F值的设置平衡精确度与搜索范围。

这里我们使用 举例：从种群中随机抽取 a=(-0.3, 0.2), b=(0.1, 0.4), c=(0.9, -0.6) 这三个个体，变异得到的新个体n即是

重复上述过程得到一组变异个体

3.变异个体与原始种群交叉

然后我们以一定概率让新产生的变异个体与原种群中个体进行交叉重组，这个概率记作，示例中令CR=0.5

例如2中得到的变异个体让它与原始种群中的进行交叉，这意味着-0.7有50%的概率被替换为0.9，0.7有50%的概率被替换为-0.6，最终我们得到的一个可能结果是 ，即0.7被替换为-0.6.

重复上述过程，我们得到了与原始种群交叉过后的新变异种群，

4.从变异个体和原始种群中筛选优秀个体

最后通过计算目标函数值，比较原始种群以及变异种群中的个体，选出下一代的原始种群。

例如原始种群中个体与变异种群个体进行比较，前者的目标函数值是1.17，后者的目标函数值是0.85，后者更接最小值点，因此我们选择保留变异个体n，替换掉前者的个体，作为新的原始种群。

 

按照上述2-4步骤进行迭代后，得到的种群逐渐接近函数的最小值点，这个迭代次数可以由参数Round控制，更大的迭代次数可以使得收敛效果提高。最终我们只需要输出种群中目标函数值最小的个体即可。

Python代码

Github传送门

import numpy as np
import random

class Population:
    def __init__(self, min_range, max_range, dim, factor, rounds, size, object_func, CR=0.75):
        self.min_range = min_range
        self.max_range = max_range
        self.dimension = dim
        self.factor = factor
        self.rounds = rounds
        self.size = size
        self.cur_round = 1
        self.CR = CR
        self.get_object_function_value = object_func
        # 初始化种群
        self.individuality = [np.array([random.uniform(self.min_range, self.max_range) for s in range(self.dimension)]) for tmp in range(size)]
        self.object_function_values = [self.get_object_function_value(v) for v in self.individuality]
        self.mutant = None

    def mutate(self):
        self.mutant = []
        for i in range(self.size):
            r0, r1, r2 = 0, 0, 0
            while r0 == r1 or r1 == r2 or r0 == r2 or r0 == i:
                r0 = random.randint(0, self.size-1)
                r1 = random.randint(0, self.size-1)
                r2 = random.randint(0, self.size-1)
            tmp = self.individuality[r0] + (self.individuality[r1] - self.individuality[r2]) * self.factor
            for t in range(self.dimension):
                if tmp[t] > self.max_range or tmp[t] < self.min_range:
                    tmp[t] = random.uniform(self.min_range, self.max_range)
            self.mutant.append(tmp)

    def crossover_and_select(self):
        for i in range(self.size):
            Jrand = random.randint(0, self.dimension)
            for j in range(self.dimension):
                if random.random() > self.CR and j != Jrand:
                    self.mutant[i][j] = self.individuality[i][j]
                tmp = self.get_object_function_value(self.mutant[i])
                if tmp < self.object_function_values[i]:
                    self.individuality[i] = self.mutant[i]
                    self.object_function_values[i] = tmp

    def print_best(self):
        m = min(self.object_function_values)
        i = self.object_function_values.index(m)
        print("轮数：" + str(self.cur_round))
        print("最佳个体：" + str(self.individuality[i]))
        print("目标函数值：" + str(m))

    def evolution(self):
        while self.cur_round < self.rounds:
            self.mutate()
            self.crossover_and_select()
            self.print_best()
            self.cur_round = self.cur_round + 1

#测试部分
if __name__ == "__main__":
    def f(v):
        return -(v[1]+47)*np.sin(np.sqrt(np.abs(v[1]+(v[0]/2)+47))) - v[0] * np.sin(np.sqrt(np.abs(v[0]-v[1]-47)))
    p = Population(min_range=-513, max_range=513, dim=2, factor=0.8, rounds=100, size=100, object_func=f)
    p.evolution()

使用函数

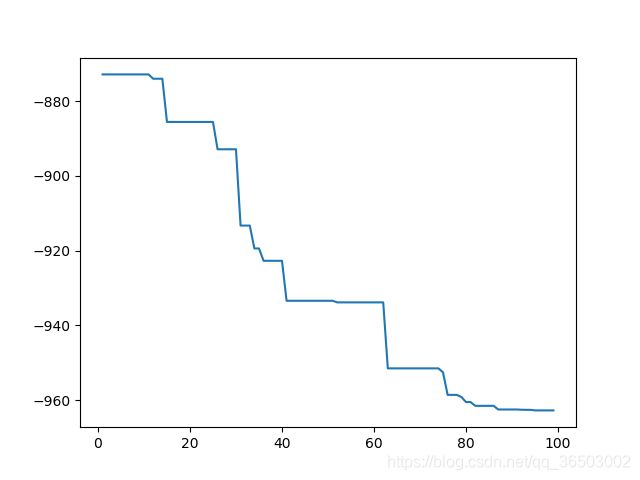
作为目标函数，迭代次数为100轮，缩放因子0.8，种群大小为100，交叉概率0.75，给定范围为 (-513, 513) 优化过程输出结果为：

轮数：1
最佳个体：[493.01612105 447.47813495]
目标函数值：-890.8481390250429
轮数：2
最佳个体：[493.01612105 447.47813495]
目标函数值：-890.8481390250429
轮数：3
最佳个体：[493.01612105 447.47813495]
目标函数值：-890.8481390250429
轮数：4
最佳个体：[493.01612105 447.47813495]
目标函数值：-890.8481390250429
轮数：5
最佳个体：[493.01612105 447.47813495]
目标函数值：-890.8481390250429

………………

轮数：96
最佳个体：[512.95350587 404.43219485]
目标函数值：-962.2366145844203
轮数：97
最佳个体：[512.95350587 404.43219485]
目标函数值：-962.2366145844203
轮数：98
最佳个体：[512.95350587 404.43219485]
目标函数值：-962.2366145844203
轮数：99
最佳个体：[512.95350587 404.43219485]
目标函数值：-962.2366145844203

目标函数值随优化轮次的变化曲线为：

求得极值点在(512.95, 404.43)