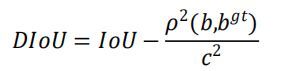手写实现IOU, CIOU, DIOU

IOU的背景

• 本文试图让您明白IOU和一些扩展复现出来加深您的理解
• IOU的发展史: L1Loss/L2Loss -> SmoothL1Loss -> IoULoss -> GIoULoss -> CIoU/DIoULoss

SmoothL1

• 最早我们使用L1loss或者L2Loss来做做boundingbox误差回归的loss函数

Faster-Rcnn作者发现

• 当误差比较大时，L2Loss容易出现梯度爆炸(平方)造成训练的不稳定,原因有可能是脏数据
• 当误差比较小时，L1Loss的梯度是常量值1，本身已经接近真值，梯度为1太- 大，容易出现在0点周围震荡
• 而误差大时，使用L1Loss梯度为1，能够稳定训练过程。误差小时，L2Loss的梯度为2x，随着误差变小而变小，接近真值时梯度也很小，更适合使用L2Loss针对误差小的情况
• 结合二者，其结果就是SmoothL1Loss干的事情

• Loss定义为：

相关公式

• $$loss(x,y)=\frac{1}{n}\sum _i{z}_i$$

• 这里的$Z_i$取值为：
  $$z_i=\{\begin{array}{ll}0.5(x_i-y_i{)}^2,& \text{if }|x_i-y_i|<1\\ |x_i-y_i|-0.5,& \text{otherwise }\end{array}$$

• 后面大家发现直接算IOU Loss来的更加直接，后面搞出GIOU, CIOU

python 魔术方法的回顾

add(self, other) 定义加法的行为：+
sub(self, other) 定义减法的行为：-
mul(self, other) 定义乘法的行为：*
truediv(self, other) 定义真除法的行为：/
floordiv(self, other) 定义整数除法的行为：//
mod(self, other) 定义取模算法的行为：%
divmod(self, other) 定义当被 divmod() 调用时的行为
pow(self, other[, modulo]) 定义当被 power() 调用或 ** 运算时的行为
lshift(self, other) 定义按位左移位的行为：<<
rshift(self, other) 定义按位右移位的行为：>>
and(self, other) 定义按位与操作的行为：&
xor(self, other) 定义按位异或操作的行为：^
or(self, other) 定义按位或操作的行为：|

boundingbox python 代码 (by Hope)

import math

def euclidean_distance(p1, p2):
    '''
    计算两个点的欧式距离
    '''
    x1, y1 = p1
    x2, y2 = p2
    return math.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)

class BBox:
    def __init__(self, x, y, r, b):
        self.x, self.y, self.r, self.b = x, y, r, b
    
    def __xor__(self, other):
        '''
        计算box和other的IoU
        '''
        cross = self & other
        union = self | other
        return cross / (union + 1e-6)
    
    def __or__(self, other):
        '''
        计算box和other的并集
        '''
        cross = self & other
        union = self.area + other.area - cross
        return union
        
    def __and__(self, other):
        '''
        计算box和other的交集
        '''
        xmax = min(self.r, other.r)
        ymax = min(self.b, other.b)
        xmin = max(self.x, other.x)
        ymin = max(self.y, other.y)
        return BBox(xmin, ymin, xmax, ymax).area
    
    def boundof(self, other):
        '''
        计算box和other的边缘外包框，使得2个box都在框内的最小矩形
        '''
        xmin = min(self.x, other.x)
        ymin = min(self.y, other.y)
        xmax = max(self.r, other.r)
        ymax = max(self.b, other.b)
        return BBox(xmin, ymin, xmax, ymax)
    
    def center_distance(self, other):
        '''
        计算两个box的中心点距离
        '''
        return euclidean_distance(self.center, other.center)
    
    def bound_diagonal_distance(self, other):
        '''
        计算两个box的bound的对角线距离
        '''
        bound = self.boundof(other)
        return euclidean_distance((bound.x, bound.y), (bound.r, bound.b))
    
    @property
    def center(self):
        return (self.x + self.r) / 2, (self.y + self.b) / 2
        
    @property
    def area(self):
        return self.width * self.height
    
    @property
    def width(self):
        return self.r - self.x
    
    @property
    def height(self):
        return self.b - self.y
    
    def __repr__(self):
        return f"{self.x}, {self.y}, {self.r}, {self.b}"

IOU实现

• IOU（交并比）是指预测边界框与真实边界框相交部分与预测边界框与真实边界框并集的比例。这是一种常用于目标检测的度量，值接近1表示预测边界框与真实边界框有较好的重叠。

def IoU(a, b):
    return a ^ b

a = BBox(10, 10, 100, 200)
b = BBox(50, 50, 150, 180)
IoU(a, b)

实现GIOU

GIoU（广义交并比）是IOU的扩展，它还考虑了预测边界框和真实边界框并集以外的区域。这有助于提高度量的准确性，当边界框的大小或形状显着不同时。

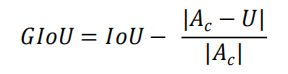
def GIoU(a, b):
    bound_area = a.boundof(b).area
    union_area = a | b
    return IoU(a, b) - (bound_area - union_area) / bound_area

GIoU(a, b)

实现DIOU

• DIoU（距离交并比）类似于IOU，但它还考虑了预测边界框和真实边界框的中心点之间的距离。当边界框远离时，这有助于提高度量的准确性。

def DIoU(a, b):
    d = a.center_distance(b)
    c = a.bound_diagonal_distance(b)
    return IoU(a, b) - (d ** 2) / (c ** 2)

DIoU(a, b)

实现CIOU

• （完整交并比）是IOU的扩展，它还考虑了边界框的大小和形状。它旨在对边界框的尺度和宽高比变化更加稳健。
• 

def CIoU(a, b):
    v = 4 / (math.pi ** 2) * (math.atan(a.width / a.height) - math.atan(b.width / b.height)) ** 2
    iou = IoU(a, b)
    alpha = v / (1 - iou + v)
    return DIoU(a, b) - alpha * v

CIoU(a, b)

总的来说，这些度量有助于评估目标检测算法的性能，并且可以用于比较不同目标检测方法的结果。