利用python通过三点法计算两个坐标系之间的位姿变换矩阵

calPoseFrom3Points

功能

已知坐标系a的原点、x轴正半轴上任一点和y轴正半轴上任一点在坐标系b下的坐标，求解坐标系a到坐标系b的旋转矩阵R和平移矩阵T。

原理

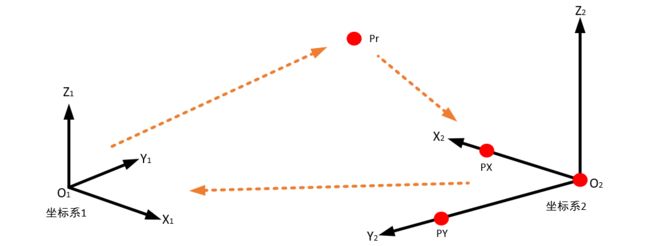
如图所示，点$$O_2$$为坐标系2的原点，$$P_X$$、$$P_Y$$分别在坐标系2的x、y轴的正半轴上。

由点$P{X}_1、P{Y}_1、O_{21}$三点构造出一个坐标系3（$P{X}_1、P{Y}_1、O_{21}$为坐标系1下各点的坐标），即$O_{21}-X_3{Y}_3{Z}_3$，坐标系3的XYZ轴指向与坐标系2相同。其中，$O_{21}$为坐标系3原点，$O_{21}$指向$P{X}_1$为X轴正方向，$O_{21}$指向$P{Y}_1$为Y轴正方向，Z轴由X轴和Y轴叉乘得到。即：
$$O21P{X}_1=P{X}_1-O21$$
$$O21P{Y}_1=P{Y}_1-O21$$
$$O21P{Z}_1=O21P{X}_1\times O21P{Y}_1$$

单位化：
$$O{X}_1=O21P{X}_1/||O21P{X}_1||$$
$$O{Y}_1=O21P{Y}_1/||O21P{Y}_1||$$
$$O{Z}_1=O21P{Z}_1/||O21P{Z}_1||$$

记：
$$O{X}_1=(a_1,b_1,c_1)$$
$$O{Y}_1=(a_2,b_2,c_2)$$
$$O{Z}_1=(a_3,b_3,c_3)$$

$O{X}_1,O{Y}_1,O{Z}_1$在坐标系3中的矢量表示为：
$$O{X}_3=(1,0,0)$$
$$O{Y}_3=(0,1,0)$$
$$O{Z}_3=(0,0,1)$$

坐标系3到坐标系1的旋转矩阵为：
$$R_{31}=\left[\begin{array}{ccc}{a}_1& a_2& a_3\\ b_1& b_2& b_3\\ c_1& c_2& c_3\end{array}\right]$$
由于坐标系3坐标轴指向与坐标系2坐标轴指向完全相同，因此坐标系3与坐标系2的旋转矩阵为单位矩阵，所以坐标系2到坐标系1的旋转矩阵$R_{21}=R_{31}$。

由于$O_{21}=R_{21}\cdot O_2+T$且$O_2=(0,0,0)$，因此$T_{21}=O_{21}$

使用

输入

坐标系a的原点在坐标系b下的坐标$O_{ab}(x_1,y_1,z_1)$

坐标系a的x轴正半轴上任一点在坐标系b下的坐标$P_{xb}(x_2,y_2,z_2)$

坐标系a的y轴正半轴上任一点在坐标系b下的坐标$P_{xb}(x_3,y_3,z_3)$

输出

坐标系a到坐标系b的旋转矩阵$R_{ab}$和平移矩阵$T_{ab}$

DEMO

import geomeas as gm
import numpy as np

Oab = np.array([-37.84381632, 152.36389864, 41.68600167])
Pxb = np.array([-19.59820338, 139.58818292, 45.55380309])
Pyb = np.array([-38.23270656, 157.3130709, 59.86810327])

print(gm.Pose().calPoseFrom3Points(Oab, Pxb, Pyb))

链接

https://gitee.com/huangzhexiaohao/geo-meas/blob/master/src/geomeas.py