反卷积的计算与加速
反卷积的计算与加速
-
- 介绍
- 插值补零法
- 交错相加法
- 小卷积核法
介绍
反卷积(标准叫法为转置卷积),是卷积的一种逆运算(注意:是卷积的逆运算,不是卷积的逆过程),属于上采样的一种,在计算机视觉的深度学习领域中被广泛用作超分辨率重建等。反卷积的详细推导过程可以看这篇。反卷积(Transposed Convolution)详细推导
本文将介绍三种反卷积计算方法(三种计算方法在数学上完全等价),并且简述每种方法的优劣。可以根据不同的加速平台选择不同的计算部署方法。
首先我们列举几个参数如下,
i : i n p u t s i z e o : o u t p u t s i z e k d : k e r n e l s i z e o f d e c o n v s d : s t r i d e o f d e c o n v p d : p a d d i n g o f d e c o n v \begin{aligned} i:&input\ size \\ o:&output\ size \\ k_d:&kernel\ size\ of \ deconv \\ s_d:&stride\ of\ deconv \\ p_d:&padding\ of\ deconv \end{aligned} i:o:kd:sd:pd:input sizeoutput sizekernel size of deconvstride of deconvpadding of deconv
其中 k d k_d kd, s d s_d sd分别是反卷积的kernel size和stride, s d s_d sd可以理解为feature map的放大倍数(在实际的超分网络中 s d s_d sd常见为2,3,4,分别代表将feature map放大2倍,3倍,4倍)。
在本文介绍的每个方法下面用一个相同的例子来说明这些算法的等价性(golden数据采用TF的计算方式):
input( i = 3 × 3 i=3\times 3 i=3×3): [ 1 2 3 4 5 6 7 8 9 ] \left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{matrix} \right] ⎣⎡147258369⎦⎤,
kernel( k d × k d = 3 × 3 k_d\times k_d= 3\times 3 kd×kd=3×3): [ 1 0 1 − 1 1 0 0 − 1 0 ] \left[ \begin{matrix} 1 & 0 & 1 \\ -1 & 1 & 0 \\ 0 & -1 & 0 \\ \end{matrix} \right] ⎣⎡1−1001−1100⎦⎤,
stride( s d = 2 s_d=2 sd=2),
output( o = 6 × 6 o=6\times 6 o=6×6): [ 1 0 3 0 5 0 − 1 1 − 2 2 − 3 3 4 − 1 9 − 2 11 − 3 − 4 4 − 5 5 − 6 6 7 − 4 15 − 5 17 − 6 − 7 7 − 8 8 − 9 9 ] \left[ \begin{matrix} 1 & 0 & 3 & 0 & 5 & 0 \\ -1 & 1 & -2 & 2 & -3 & 3 \\ 4 & -1 & 9 & -2 & 11 & -3 \\ -4 & 4 & -5 & 5 & -6 & 6 \\ 7 & -4 & 15 & -5 & 17 & -6 \\ -7 & 7 & -8 & 8 & -9 & 9 \\ \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎡1−14−47−701−14−473−29−515−802−25−585−311−617−903−36−69⎦⎥⎥⎥⎥⎥⎥⎤ (TF1.15计算结果)
插值补零法
此计算方法是目前最常见的计算反卷积的方法,核心思想就是在input feature map里的每个pixel之间插 0 0 0,将kernel在二维平面旋转180°,然后进行 k e r n e l = k d , s t r i d e = 1 kernel=k_d,stride=1 kernel=kd,stride=1的常规卷积计算。其中 0 0 0的个数 n n n 与 s d s_d sd有关,具体数学关系为:
n = s t r i d e − 1 n=stride-1 n=stride−1
此时反卷积的输入输出尺寸关系为:
o = s d ( i − 1 ) − 2 p d + k d o=s_d(i-1)-2p_d+k_d o=sd(i−1)−2pd+kd
实际用tensorflow或者其他框架进行反卷积计算时,必须指定输出图像的大小 o o o,参考崔权:关于tf中的conv2d_transpose的用法,tensorflow反卷积层中也没有 p d p_d pd这个参数( 注:TF中的padding只有’SAME’和’VALID’两种模式),我个人理解实际计算中的 p d p_d pd应该是由 i , o , s d , k d i,o,s_d,k_d i,o,sd,kd反推出来的。
让我们来看下面两张采用插值补零法的反卷积计算动图:
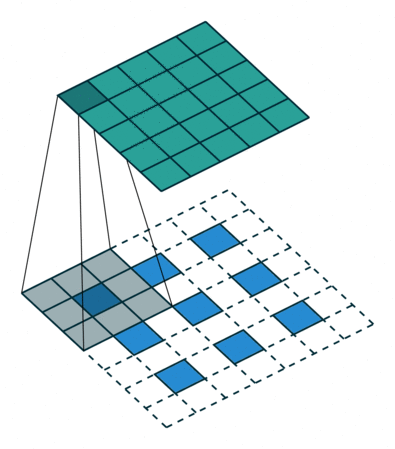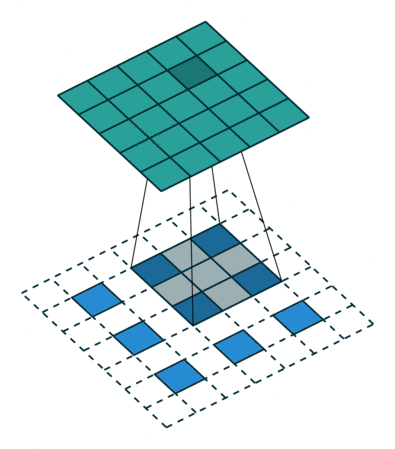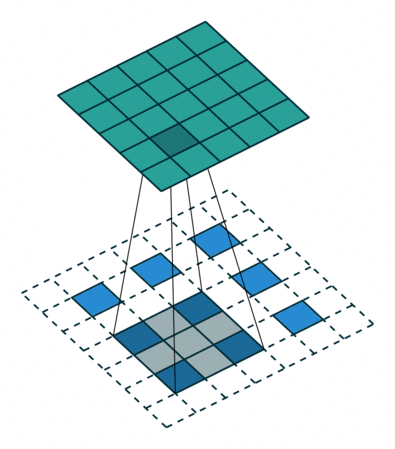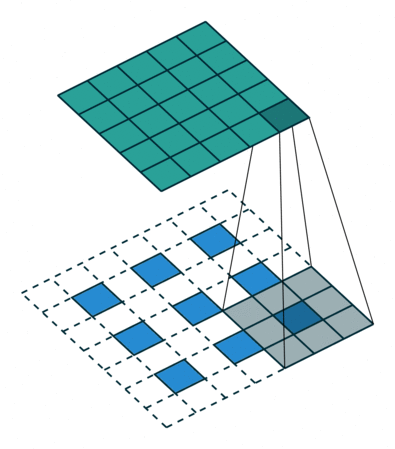
上图中 i = 3 , o = 5 , k d = 3 , s d = 3 i=3,o=5,k_d=3,s_d=3 i=3,o=5,kd=3,sd=3,因此可以推算出该反卷积在top、bottom、left、right都补了1个 0 0 0。

上图中 i = 3 , o = 6 , k d = 3 , s d = 3 i=3,o=6,k_d=3,s_d=3 i=3,o=6,kd=3,sd=3,因此可以推算出该反卷积在top、left补了1个 0 0 0,而在bottom、right补了2个 0 0 0注:TF的计算规则是优先在top、left补2个 0 0 0,在bottom、right补1个 0 0 0)。
回到我们的例子,我们采用插值补零法计算反卷积的过程如下,
输入input插值补零(根据TF的计算规则): [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 2 0 3 0 0 0 0 0 0 0 0 0 0 0 4 0 5 0 6 0 0 0 0 0 0 0 0 0 0 0 7 0 8 0 9 0 0 0 0 0 0 0 0 0 ] \left[ \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 2 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 4 & 0 & 5 & 0 & 6 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 7 & 0 & 8 & 0 & 9 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡0000000000000000001040700000000000205080000000000030609000000000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤ ,
deconv kernel旋转180°: [ 0 − 1 0 0 1 − 1 1 0 1 ] \left[ \begin{matrix} 0 & -1 & 0 \\ 0 & 1 & -1 \\ 1 & 0 & 1 \\ \end{matrix} \right] ⎣⎡001−1100−11⎦⎤,
最后正向卷积得: [ 1 0 3 0 5 0 − 1 1 − 2 2 − 3 3 4 − 1 9 − 2 11 − 3 − 4 4 − 5 5 − 6 6 7 − 4 15 − 5 17 − 6 − 7 7 − 8 8 − 9 9 ] \left[ \begin{matrix} 1 & 0 & 3 & 0 & 5 & 0 \\ -1 & 1 & -2 & 2 & -3 & 3 \\ 4 & -1 & 9 & -2 & 11 & -3 \\ -4 & 4 & -5 & 5 & -6 & 6 \\ 7 & -4 & 15 & -5 & 17 & -6 \\ -7 & 7 & -8 & 8 & -9 & 9 \\ \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎡1−14−47−701−14−473−29−515−802−25−585−311−617−903−36−69⎦⎥⎥⎥⎥⎥⎥⎤ ,
可以看出和TF golden结果一致。
优点:将反卷积转化成常规卷积,可以用专用的卷积加速器(NPU、DPU等各种xPU)进行加速计算。
缺点:需要在每个pixel间插0,那么从外部存储器(DDR)读取数据就会不连续,容易形成带宽bound;计算中也有很多冗余计算(乘0累加),实际计算效率(computation efficiency)也很低。
交错相加法
此方法是名符其实的“反”卷积,让我们回想下二维卷积的计算方法,一个 k × k k\times k k×k 的卷积核在以 stride 的间隔距离滑过input feature map,每一次滑动做一次卷积核和滑窗pixel的乘累加计算,并且得到一个output feature map中的一个pixel,如下图所示:
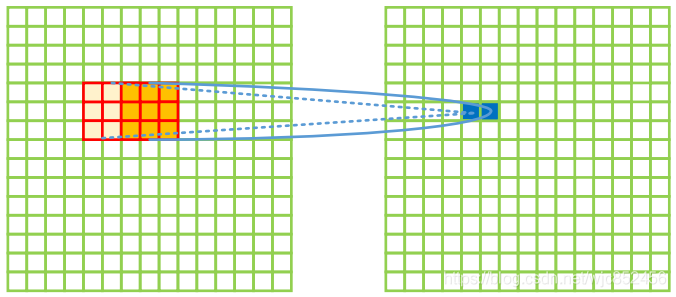
反卷积的计算就是正向卷积计算的逆向操作,先放图:

具体计算过程就是input feature map上的每一个pixel和 k × k k\times k k×k 的卷积核点乘得到一个 k × k k\times k k×k的patch,然后相邻的patch以间隔 stride 错位相加,如上图所示。一般来说,这种计算方法还需要对边界进行裁剪以符合output feature map的大小 o o o 。这种计算过程正好和正向的卷积计算是“反”过来的,故名“反卷积”(大雾)。
我们还是以计算为例,input每个pixel和反卷积核点乘得到9个 3 × 3 3\times 3 3×3 patch:
[ 1 0 1 − 1 1 0 0 − 1 0 ] , [ 2 0 2 − 2 2 0 0 − 2 0 ] , [ 3 0 3 − 3 3 0 0 − 3 0 ] \left[ \begin{matrix} 1 & 0 & 1 \\ -1 & 1 & 0 \\ 0 & -1 & 0 \\ \end{matrix} \right] , \left[ \begin{matrix} 2 & 0 & 2 \\ -2 & 2 & 0 \\ 0 & -2 & 0 \\ \end{matrix} \right] , \left[ \begin{matrix} 3 & 0 & 3 \\ -3 & 3 & 0 \\ 0 & -3 & 0 \\ \end{matrix} \right] ⎣⎡1−1001−1100⎦⎤,⎣⎡2−2002−2200⎦⎤,⎣⎡3−3003−3300⎦⎤ ,
[ 4 0 4 − 4 4 0 0 − 4 0 ] , [ 5 0 5 − 5 5 0 0 − 5 0 ] , [ 6 0 6 − 6 6 0 0 − 6 0 ] \left[ \begin{matrix} 4 & 0 & 4 \\ -4 & 4 & 0 \\ 0 & -4 & 0 \\ \end{matrix} \right] , \left[ \begin{matrix} 5 & 0 & 5 \\ -5 & 5 & 0 \\ 0 & -5 & 0 \\ \end{matrix} \right] , \left[ \begin{matrix} 6 & 0 & 6 \\ -6 & 6 & 0 \\ 0 & -6 & 0 \\ \end{matrix} \right] ⎣⎡4−4004−4400⎦⎤,⎣⎡5−5005−5500⎦⎤,⎣⎡6−6006−6600⎦⎤ ,
[ 7 0 7 − 7 7 0 0 − 7 0 ] , [ 8 0 8 − 8 8 0 0 − 8 0 ] , [ 9 0 9 − 9 9 0 0 − 9 0 ] \left[ \begin{matrix} 7 & 0 & 7 \\ -7 & 7 & 0 \\ 0 & -7 & 0 \\ \end{matrix} \right] , \left[ \begin{matrix} 8 & 0 & 8 \\ -8 & 8 & 0 \\ 0 & -8 & 0 \\ \end{matrix} \right] , \left[ \begin{matrix} 9 & 0 & 9 \\ -9 & 9 & 0 \\ 0 & -9 & 0 \\ \end{matrix} \right] ⎣⎡7−7007−7700⎦⎤,⎣⎡8−8008−8800⎦⎤,⎣⎡9−9009−9900⎦⎤ ,
相邻patch以 stride=2 错位相加得: [ 1 0 3 0 5 0 3 − 1 1 − 2 2 − 3 3 0 4 − 1 9 − 2 11 − 3 6 − 4 4 − 5 5 − 6 6 0 7 − 4 15 − 5 17 − 6 9 − 7 7 − 8 8 − 9 9 0 0 − 7 0 − 8 0 − 9 0 ] \left[ \begin{matrix} 1 & 0 & 3 & 0 & 5 & 0 & 3\\ -1 & 1 & -2 & 2 & -3 & 3 & 0 \\ 4 & -1 & 9 & -2 & 11 & -3 & 6 \\ -4 & 4 & -5 & 5 & -6 & 6 & 0\\ 7 & -4 & 15 & -5 & 17 & -6 & 9\\ -7 & 7 & -8 & 8 & -9 & 9 & 0\\ 0 & -7 & 0 & -8 & 0 & -9 & 0\\ \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡1−14−47−7001−14−47−73−29−515−8002−25−58−85−311−617−9003−36−69−93060900⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤ ,
对最右列和最底行进行裁剪得到最终结果: [ 1 0 3 0 5 0 − 1 1 − 2 2 − 3 3 4 − 1 9 − 2 11 − 3 − 4 4 − 5 5 − 6 6 7 − 4 15 − 5 17 − 6 − 7 7 − 8 8 − 9 9 ] \left[ \begin{matrix} 1 & 0 & 3 & 0 & 5 & 0 \\ -1 & 1 & -2 & 2 & -3 & 3 \\ 4 & -1 & 9 & -2 & 11 & -3 \\ -4 & 4 & -5 & 5 & -6 & 6 \\ 7 & -4 & 15 & -5 & 17 & -6 \\ -7 & 7 & -8 & 8 & -9 & 9 \\ \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎡1−14−47−701−14−473−29−515−802−25−585−311−617−903−36−69⎦⎥⎥⎥⎥⎥⎥⎤ 。
可以看出和TF golden结果一致。
优点:没有任何的冗余计算,不需要对输入补0。
缺点:无法利用专用的卷积加速器进行加速,但是适合用CPU或GPU这种比较通用的处理器进行计算(注:caffe的反卷积采用的就是此计算方法)。
小卷积核法
此方法是本人最为欣赏的一个方法,该方法将每一个大小为 k d × k d k_d\times k_d kd×kd 的反卷积核先在二维方向旋转180°,然后再将每一个反卷积核拆成 s d × s d s_d\times s_d sd×sd 个小卷积核(注:此时我们可以认为 c o c_o co 扩大了 s d × s d s_d\times s_d sd×sd 倍),然后用这些小卷积核对input feature map做 s t r i d e = 1 stride=1 stride=1 的正向卷积,最后通过depth2space将 c o c_o co方向的pixel重排到二维平面上。具体过程如下图示:

上图kernel=3,stride=2的反卷积,我们先将其分拆并重排成4个kernel=2,stride=1的正向卷积核,重排方案如下:

图中的0-8代表二维 3 × 3 3\times 3 3×3 deconv kernel每个点的index(注:-1代表这个位置没有值且补零)。
接着用这些正向卷积核对input feature map做正向卷积,得到4个output feature map,再用depth2space将 c_o 方向的数据重排到二维平面上。如下图所示:

反卷积核的重排可以离线完成,不占用计算时间也不占用带宽。
回到我们的例子,deconv kernel拆成4个kernel=2的小卷积核:
[ 0 0 1 1 ] \left[ \begin{matrix} 0 & 0 \\ 1 & 1 \\ \end{matrix} \right] [0101] , [ 0 − 1 0 0 ] \left[ \begin{matrix} 0 & -1 \\ 0 & 0 \\ \end{matrix} \right] [00−10] , [ 0 0 0 − 1 ] \left[ \begin{matrix} 0 & 0 \\ 0 & -1 \\ \end{matrix} \right] [000−1] , [ 0 0 0 1 ] \left[ \begin{matrix} 0 & 0 \\ 0 & 1 \\ \end{matrix} \right] [0001] ,
对input的左列和上行进行1次padding: [ 0 0 0 0 0 1 2 3 0 4 5 6 0 7 8 9 ] \left[ \begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 2 & 3 \\ 0 & 4 & 5 & 6 \\ 0 & 7 & 8 & 9 \\ \end{matrix} \right] ⎣⎢⎢⎡0000014702580369⎦⎥⎥⎤ ,
用每个小卷积核对上面padding过的input进行stride=1的正向卷积得:
[ 1 3 5 4 9 11 7 15 17 ] \left[ \begin{matrix} 1 & 3 & 5 \\ 4 & 9 & 11 \\ 7 & 15 & 17 \\ \end{matrix} \right] ⎣⎡147391551117⎦⎤ , [ 0 0 0 − 1 − 2 − 3 − 4 − 5 − 6 ] \left[ \begin{matrix} 0 & 0 & 0 \\ -1 & -2 & -3 \\ -4 & -5 & -6 \\ \end{matrix} \right] ⎣⎡0−1−40−2−50−3−6⎦⎤ , [ − 1 − 2 − 3 − 4 − 5 − 6 − 7 − 8 − 9 ] \left[ \begin{matrix} -1 & -2 & -3 \\ -4 & -5 & -6 \\ -7 & -8 & -9 \\ \end{matrix} \right] ⎣⎡−1−4−7−2−5−8−3−6−9⎦⎤ , [ 1 2 3 4 5 6 7 8 9 ] \left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{matrix} \right] ⎣⎡147258369⎦⎤ ,
以上结果可以看成是4个通道的feature map,最后进行depth2space得:
[ 1 0 3 0 5 0 − 1 1 − 2 2 − 3 3 4 − 1 9 − 2 11 − 3 − 4 4 − 5 5 − 6 6 7 − 4 15 − 5 17 − 6 − 7 7 − 8 8 − 9 9 ] \left[ \begin{matrix} 1 & 0 & 3 & 0 & 5 & 0 \\ -1 & 1 & -2 & 2 & -3 & 3 \\ 4 & -1 & 9 & -2 & 11 & -3 \\ -4 & 4 & -5 & 5 & -6 & 6 \\ 7 & -4 & 15 & -5 & 17 & -6 \\ -7 & 7 & -8 & 8 & -9 & 9 \\ \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎡1−14−47−701−14−473−29−515−802−25−585−311−617−903−36−69⎦⎥⎥⎥⎥⎥⎥⎤。
可以看出和TF golden结果一致。
优点:可以用专用的卷积加速器加速反卷积计算,没有带宽bound。
缺点:卷积核重排比较复杂,没有统一的方案,部分卷积加速器可能不支持depth2space。