反向传播代码

线性模型和梯度下降_BKXjilu的博客-CSDN博客前面学习了简单的模型和求梯度的方法，反向传播可以用于复杂的模型。

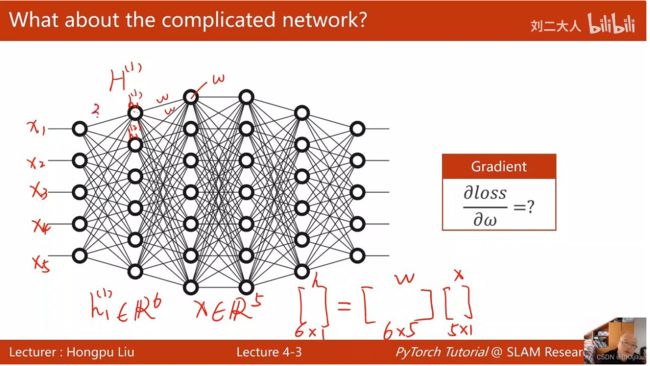
复杂模型是怎么层层计算的？

x为输入，H为节点。表示第一列的结点

下图有5个输入x=，第一层有6个结点，第二层有7个结点，结构复杂。 

h=w*x，w是六行五列的矩阵。第一层得到的h变成下一层的输入。

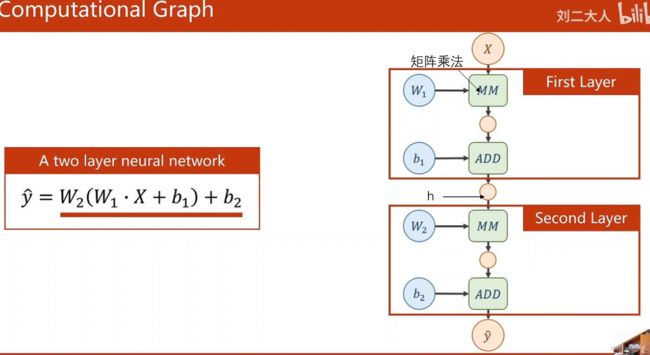
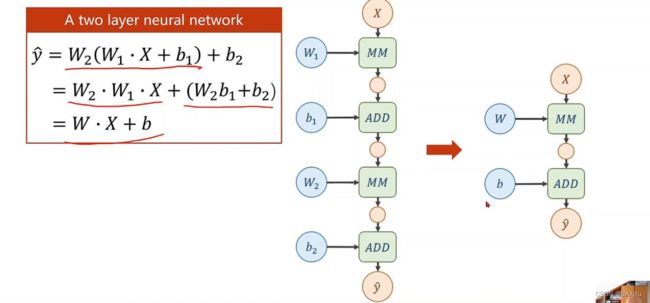
如下图可以看出经过层层的计算，y仍然是线性函数，这样的模型不具备模拟复杂函数的能力。

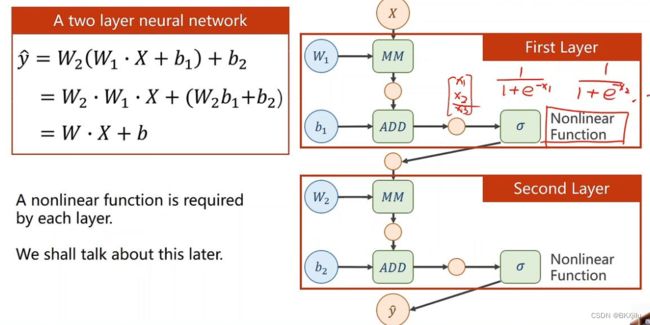
 所以需要我们对每层的输出结果h加上非线性的变化函数。 

对每个x做 

 反向传播怎么计算梯度？

使用链式法则：

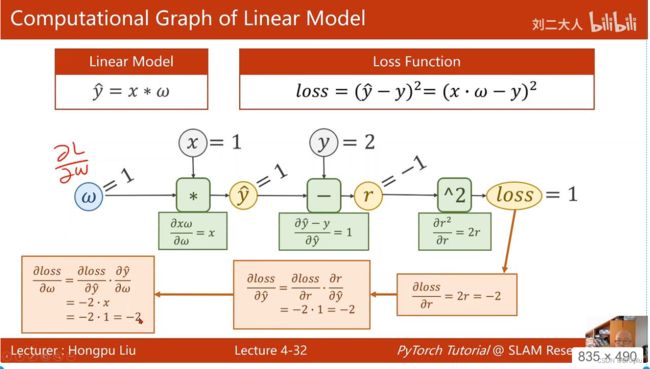
对于y=w*x模型：

r是残差。前向传播过程（绿色方框部分）：对于求梯度有关的量，r，loss进行求导；

反向传播过程，根据链式法则和前向传播的导数值求解梯度。

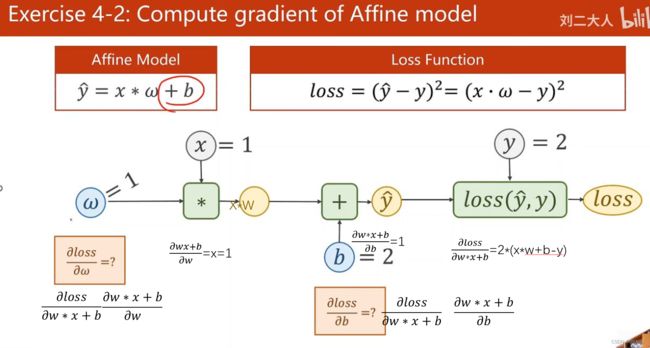
对于y=w*x+b模型：

Tensor :可以存标量，向量，矩阵。

Tensor包括data和grad。

data放置权重的值，grad放置导数值 

反向传播代码： 

1.选择权重w，torch,Tesnsor 类似np.array创建一个数组。

2.说明w需要计算梯度，Tensor创建默认是不进行梯度计算的。

3.选择的是随机梯度下降法，loss表示某个样本点的损失函数。

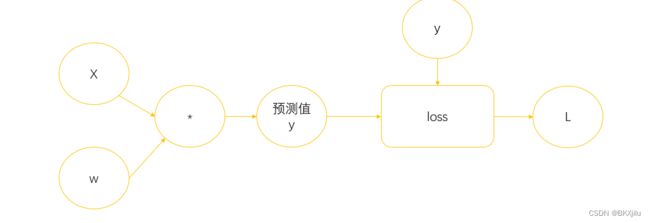
loss函数在构建计算图：

4.w*x ,x是Tensor,*被重载（重载就是原本“*”进行数和数的乘法，重载之后可以进行矩阵和矩阵的乘法），w*x进行矩阵乘法，x会自动进行转换，变成Tensor。

5.前向传播：l=loss(x,y)计算损失，得到的l是一个张量。（普通的矩阵就是二维张量，数组就是一维张量，空间矩阵就是三维张量，类似的，还有四维、五维、六维张量）

6.前向传播产生l张量，l.backword()将计算图中所有梯度。然后把梯度存到w里面，接下来计算图被释放。根据下一组（x,y)再计算loss的时候会产生新的计算图。

对当前这道题来说，只有一个权重w,计算图是一样的，释放与否没什么区别；但是对于有多个权重的情况，计算图可能不同，需要释放计算图。

7.w.grad.item()是直接把w.grad的数值取出，变成一个标量；w.grad.data取值（data也是Tensor，但是不构建计算图）。因为w.grad取得是Tensor,会产生计算图，这样中做法是为了避免产生计算图。

？data和.item()有什么区别(14条消息) 编程速记(35)：Pytorch篇-.item()与.data的区别_Leeyegy的博客-CSDN博客_item和data

8.清零w的梯度值。如果没有清零w.grad.data,会在第一次梯度的基础上加第二次计算的梯度。

import matplotlib.pyplot as plt
import torch
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]
#w为Tensor Tensor表示变量或向量
w = torch.Tensor([1.0])
#说明w要计算梯度
w.requires_grad = True
epoch1=[]
item=[]
#计算随机梯度
def forward(x):
    return w*x
def loss(x,y):
    y_pre = forward(x)
    loss = (y_pre-y)**2
    return loss

for epoch in range(100):
    for x,y in zip(x_data,y_data):
        #Tensor l
        l=loss(x,y)
        #反向传播
        l.backward()
        #打印x，y,w的梯度的数值
        print('\tgrad:',x,y,w.grad.item())
        #得到梯度数据，更新w
        w.data = w.data - 0.01*w.grad.data
        #数据清零
        w.grad.data.zero_()
    print("progress:",epoch,l.item())
    epoch1.append(epoch)
    item.append(l.item())
print("predict (after training)",4,forward(4).item())
plt.plot(epoch1,item)
plt.ylabel('item')
plt.xlabel('epoch')
plt.show()

 

课后作业： 

w = torch.Tensor([1.0,1,0,1.0]),w里面顺序存放w1,w2,b.

使用索引表示：w1=w[0],w2=w[1],b=w[2]

其他选取tensor中值的方法

例解tensor.gather() - 知乎 (zhihu.com)

import matplotlib.pyplot as plt
import torch
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]
#w为Tensor Tensor表示变量或向量
w = torch.Tensor([1.0,1,0,1.0])
#说明w要计算梯度
w.requires_grad = True
epoch1=[]
item=[]
#计算预测值
def forward(x):
    return w[0]*x*x+w[1]*x+w[2]
#计算损失
def loss(x,y):
    y_pre = forward(x)
    loss = (y_pre-y)**2
    return loss

for epoch in range(100):
    for x,y in zip(x_data,y_data):
        #Tensor l
        l=loss(x,y)
        #反向传播
        l.backward()
        #打印x，y,w的梯度的数值
        print('\tgrad:',x,y,w.grad.tolist())

        #得到梯度数据，更新w
        w.data = w.data - 0.01*w.grad.data
        #数据清零
        w.grad.data.zero_()
    print("progress:",epoch,l.item())
    epoch1.append(epoch)
    item.append(l.item())
print("predict (after training)",4,forward(4).item())
plt.plot(epoch1,item)
plt.ylabel('item')
plt.xlabel('epoch')
plt.show()