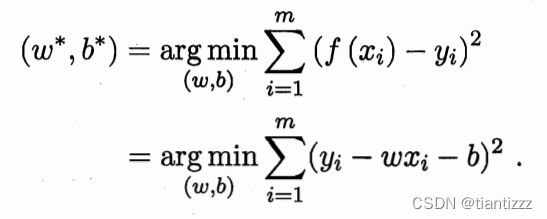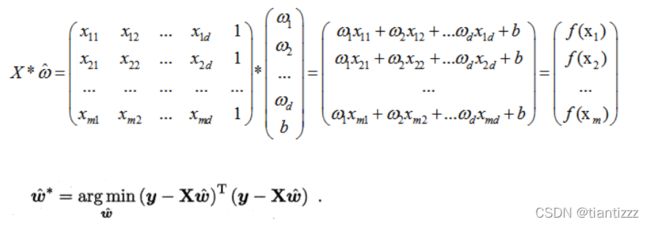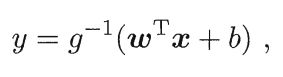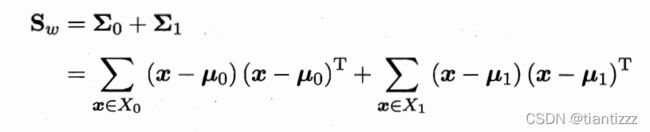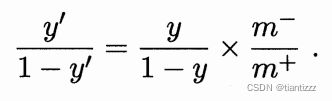《机器学习》读书笔记2--线性模型

目录

线性模型基本形式

线性回归

对数几率回归

线性判别分析

多分类学习

类别不平衡问题

---

ps.写在前面，本文是在参加datawhale组队学习，学习周志华老师的《机器学习》过程的学习笔记。文中出现的图片均引自《机器学习》，《机器学习》是初学者入门机器学习领域的很好的教材。推荐给想要入门学习机器学习领域的同路者。

线性模型基本形式

        线性模型试图学的一个通过特征属性的线性组合来进行预测的函数。可以理解为，有一组特征属性D，，其中  是  在第个属性上的取值。线性模型要通过特征属性D来确定如下这样的线性组合，其中主要目标则是确定和b。和b学得后，整个模型就得以确定。

举个简单的例子，在判断是否为好的西瓜这一问题上，我们想通过线性模型来预测，则有：

 其中的[0.2,0.5,0.3]就是，[色泽，根蒂，敲声]是属性集合D。

线性回归

        线性回归是试图学得一个线性模型（如上面的线性组合），来尽可能的准确地预测新样本的输出值。对于输入值要分为连续值和离散值两类，对于连续值后面有相应的处理方法如：归一化等，对于离散值，则我们要进行如下处理：

• 属性值间存在“序”关系，可以将其连续化转变为连续值。如：二值属性，身高的“高”，“矮”，可以转化为[1,0]，三值属性，高度取值“高”，“中”，“低”可以转化为[1.0，0.5，0.0]。
• 属性值间不存在“序”关系，则不可以转变为连续值，不然不恰当的引入序关系。假定有k个属性值，则转化为k维One-hot 向量，如性别问题：男女可转换为{(1,0),(0,1)}，瓜类的属性“西瓜”，“南瓜”，“黄瓜”可以转化为{（1,0,0）,（0,1,0）,（0,0,1）}

        线性回归的任务就是令自己的预测值尽可能的逼近真实值。如何衡量预测值和真实值之间的差距呢？则需要依靠性能度量。均方误差是回归任务中最常用的性能度量，因此我们可以令均方误差最小化使得预测值逼近真实值。

求解这个最小化的过程叫做线性模型的最小二乘参数估计，可以通过分别对和b求导，令导数为0来计算。

 上述式子可以求出和b，但是在只有一种属性的前提下。当考虑更一般的情况，即输入的属性为集合D时，则变为多元线性回归。也同样可以通过最小二乘法进行求解。

对于多元问题，常常使用矩阵的形式来表示数据，把属性集合D表示为一个矩阵，其中每一行表示一个样本，最后一列恒为1，则表示如下：

上式中求导并令其为0可以求出闭式解，但这里还需要做一些假设讨论。就是上式可以求出解的前提是为满秩矩阵或是正定矩阵，只有这样才能求逆。如果不是的话，则需要引入正则化项（后续再详述）。

对数几率回归

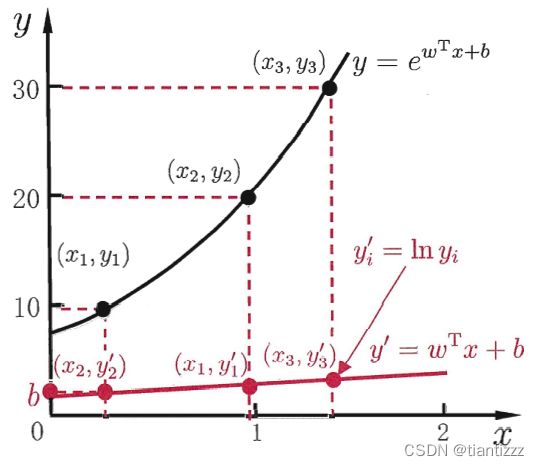
线性模型在很多时候可以简写为 . 但有些时候，输出并不一定是线性的，有可能输出是在指数尺度上变化的，那么可以将输出的对数形式作为我们线性模型预测需要逼近的目标，即,这就是对数线性回归。它试图让来逼近. 

而对数线性回归也不过是线性回归下的一种特殊形式，如果要考虑所有y的衍生物，则有广义的线性模型，

 其中g必须是单调可微的函数，并称g为联系函数，将线性回归模型的预测值与真实标记联系起来的作用。 

线性模型进行回归学习，已经有所了解了，那么如果要做的是分类任务又该如何呢？ 就是能否将输出的预测值转化为离散值从而进行分类任务呢？例如二分类我们就将其转化为（0，1）。

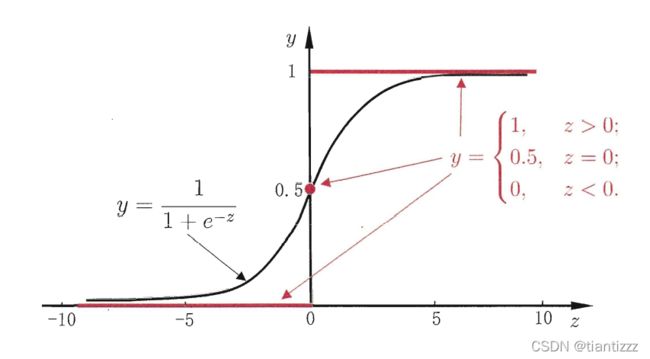
线性几率回归就是针对此类问题的，通过引入对数几率函数，将预测值转化为0-1之间从而完成分类任务。

对数几率函数是一种“Sigmoid 函数”（Sigmoid函数即形似S的函数。），将z值转化为一个接近0或1的y值，并且在z=0附近变化很陡。

线性判别分析

线性判别分析，简称LDA，是一种经典线性学习方法，主要思想是将样本投影到一条直线上，使同类样本点尽可能的靠近，异类样本点尽可能远离。

目标是让同类样本点的投影点尽可能靠近，异类样本点投影之间尽可能远离，即：让各类的协方差之和尽可能小，异类之间中心的距离尽可能大。基于这样的考虑，LDA定义了两个散度矩阵。

• 类内散度矩阵 （越小越好，越小代表同类越接近）

• 类间散度矩阵（越大越好，越大代表异类越远离）

由此，得到LDA最大化的目标，即的广义瑞丽商：

从而将分类问题，变成了求解最优化问题，当求解出W后，新样本输入进来，只需要将其投影到直线上，判断距离哪个类别最接近，就可以将样本进行分类。

多分类学习

现实中常常会遇到多分类学习的任务，我们解决问题的基本思想是“拆解法”，将多分类学习任务，拆解成若干个二分类任务求解。

主要的拆分策略有三种：

• 一对一（One vs One 简称OvO），OvO的原理是：给定一个数据集D，将其N个类别分别两两配对，从而产生N（N-1）/ 2 个二分类任务，新样本输入进来，会同时提交给所有的分类器，得到N（N-1）/ 2 个分类结果，再将其结果进行投票，把预测的最多的结果作为最终结果。
• 一对多（One vs Rest 简称OvR），OvR的原理是：给定一个数据集D，每次将一个类别的样例作为正例，其他所有类别的样例都作为反例来进行训练，则会产生N个二分类学习器，得出N个分类结果，若只有一个分类器预测为正，则对应的类别作为最终结果，若有多个分类器预测为正，则要考虑各分类器的预测置信度，选择置信度最大的作为分类结果。

• 多对多（Many vs Many 简称 MvM），MvM的原理：给定一个数据集D，每次将若干个类作为正类，若干个其他类作为反类，但其正、反类的构造必须有特殊的设计，不能随意选取。常用的MvM技术：纠错输出码（ECOC）

海明距离：简单理解就是指同一位置上编码不同的个数。

欧式距离：空间中距离公式

类别不平衡问题

类别不平衡就是指分类任务中不同类别的训练样例数差距非常大的情况。例如一组数据集D中正例样本有998个，反例样本只有2个，这样再有新样本输入，不管是正例还是反例，只要统统返回正例就可以达到很高的准确度，但这明显是不对的。所以对于类别不平衡问题我们常常需要进行额外的处理，常见的方法有：

• 对于训练样本较多的，采用欠采样，去除一些样本较多的样本，使正反例接近。代表算法EasyEnsemble，
• 对于训练样本较少的，采用过采样，重复采集样本较少的样本，使正反例接近。代表算法SMOTE，通过插值产生额外样本。
• 直接基于原始样本数据进行学习，但在用训练好的分类器进行预测时进行再缩放，也是代价敏感学习的基础。