图像修复DeepFillv1:Generative Image Inpainting with Contextual Attention(CVPR2018)
Paper:https://arxiv.org/pdf/1801.07892.pdf
Code:https://github.com/JiahuiYu/generative_inpainting/tree/v1.0.0
基于
S. Iizuka, E. Simo-Serra, and H. Ishikawa. Globally and locally consistent image completion. ACM Transactions on Graphics (TOG), 36(4):107, 2017.
contributions:
- 提出新的contextual attention layer,去关联距离较远的背景patch(关联待修复区域与较远的已知区域)。
- 提出一些trick,如global WGAN + local WGAN结合使用;空间权重衰减损失。
- 效果好
网络结构
Coarse NetWork
常规操作
输入:待修补图像 + mask(标注待修复区域)
输出:粗修复结果
Dilate Conv:增大感受野(毕竟已知区域可能距离很远,而修补只能从已知区域去获取信息,与分割检测等任务不同的是,图像修复位置本身是没语义信息的)
其他:
- 镜像padding
- remove BN(WGAN-GP中就移除了BN)
- ELU替换ReLu
- clip the output filter values instead of using tanh or sigmoid functions.(?指代哪部分,激活函数用ELU?)
- GAN训练部分,分离global部分和local部分
Spatially discounted reconstruction loss
空间权重衰减的loss:在缺失区域,“合理”的修补结果有很多种,如果只用ground truth做为唯一的衡量标准是不合理的。
从待修复区域的边缘向中心区域看,离边缘越远,其"合理"的情况会越多。而边缘部分和已知区域相连着,其纹理颜色等受已知区域限制更大,因此其可能情况会更少。
因此给边缘部分的loss更大的权重,而离边缘越远,其权重衰减越厉害。
Refinement Network
refine部分结构图如图4,输入为粗修复的图,兵分两路,下路就是多加几个卷积划划水。上路为几个卷积 + Contextual Attention Layer。
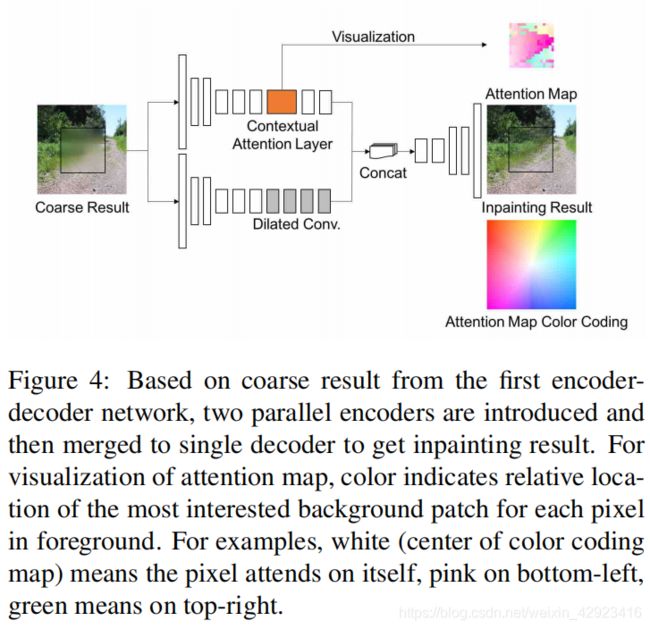
Contextual Attention
这部分就是对粗生成的区域关联已知区域,还是找和前景最相似的背景区域,然后用背景区域来辅助refine生成。
ForeGround即生成区域,将已知区域(background)的feature map划分为一个个小区域如(3 x 3)就得到上图中那橙色的长条,用这些小区域分别依次与foreground的每个部分(3 x 3)求cosine距离。分别找到与前景每个小区域最相似的背景小区域。随后依次用这些小的background做为deconvolutional filters去refine,结果重叠的部分求均值。
s x , y , x ′ , y ′ = ⟨ f x , y ∥ f x , y ∥ , b x ′ , y ′ ∥ b x ′ , y ′ ∥ ⟩ s_{x, y, x^{\prime}, y^{\prime}}=\left\langle\frac{f_{x, y}}{\left\|f_{x, y}\right\|}, \frac{b_{x^{\prime}, y^{\prime}}}{\left\|b_{x^{\prime}, y^{\prime}}\right\|}\right\rangle sx,y,x′,y′=⟨∥fx,y∥fx,y,∥bx′,y′∥bx′,y′⟩
f x , y f_{x,y} fx,y:前景, f x ′ , y ′ f_{x^{\prime},y^{\prime}} fx′,y′:背景。
s即cosine距离(归一化后点乘)

但是这个Softmax操作有点疑问,按文中意思只要知道最大值的index应该就足够了,没必要softmax吧?而且取索引操作不可导,对网络更新也没帮助。
Attention propagation
区域一致性的假设。从背景里找和前景相似的区域,找到的往往不止是一个点相似,更经常的是一整块区域相似(且无论前景还是背景,其相邻区域也总是相似的)。
因此最终的结果是一个 K x K区域内的累加和。其实现也简单,用一个全1矩阵点乘就行了(求和),这一操作significantly improves inpainting results in testing and enriches gradients in training.
s ^ x , y , x ′ , y ′ = ∑ i ∈ { − k , … , k } s x + i , y , x ′ + i , y ′ ∗ \hat{s}_{x, y, x^{\prime}, y^{\prime}}=\sum_{i \in\{-k, \ldots, k\}} s_{x+i, y, x^{\prime}+i, y^{\prime}}^{*} s^x,y,x′,y′=i∈{−k,…,k}∑sx+i,y,x′+i,y′∗
Global and local Wasserstein GANs
用改进的WGAN-GP替换之前其他网络常用的DCGAN(当时WGAN-GP loss是最好的GAN的 loss)
WGAN中用到的discriminator loss(前提是满足Lipschitz连续条件)
参考博客:https://www.cnblogs.com/Allen-rg/p/10305125.html
max D ∈ D E x ∼ P r [ D ( x ) ] − E x ~ ∼ P g [ D ( x ~ ) ] \max _{D \in \mathcal{D}} E_{\mathbf{x} \sim \mathbb{P}_{r}}[D(\mathbf{x})]-E_{\tilde{\mathbf{x}} \sim \mathbb{P}_{g}}[D(\tilde{\mathbf{x}})] D∈DmaxEx∼Pr[D(x)]−Ex~∼Pg[D(x~)]
Lipschitz连续:即定义域内没点的梯度不超过某个定值K,WGAN中的策略是对网络的权重clip成 [-c, c]区域内,因在网络中,每层的输入x的导数与权重w直接相关,权重大小限制后,其导数也即被限定在一个范围内了。
WGAN-GP与WGAN的不同在于,如何满足Lipschitz连续,即在原始discriminator loss(WGAN-GP中称critic)中,再对导数加一个L2范数。
L = E x ~ ∼ P g [ D ( x ~ ) ] − E x ∼ P r [ D ( x ) ] ⏟ Original critic loss + λ E x ^ ∼ P w ^ [ ( ∥ ∇ x ^ D ( x ^ ) ∥ 2 − 1 ) 2 ] ⏟ Our gradient penalty L=\underbrace{\underset{\tilde{\boldsymbol{x}} \sim \mathbb{P}_{g}}{\mathbb{E}}[D(\tilde{\boldsymbol{x}})]-\underset{\boldsymbol{x} \sim \mathbb{P}_{r}}{\mathbb{E}}[D(\boldsymbol{x})]}_{\text {Original critic loss }}+\underbrace{\lambda \underset{\hat{\boldsymbol{x}} \sim \mathbb{P}_{\hat{\boldsymbol{w}}}}{\mathbb{E}}\left[\left(\left\|\nabla_{\hat{\boldsymbol{x}}} D(\hat{\boldsymbol{x}})\right\|_{2}-1\right)^{2}\right]}_{\text {Our gradient penalty }} L=Original critic loss x~∼PgE[D(x~)]−x∼PrE[D(x)]+Our gradient penalty λx^∼Pw^E[(∥∇x^D(x^)∥2−1)2]
其中Our gradient penalty中, x ~ \tilde{\boldsymbol{x}} x~为生成器的输出,Our gradient penalty最终处理的 x ^ \hat{\boldsymbol{x}} x^是 x ~ \tilde{\boldsymbol{x}} x~加上部分高斯噪声,如下式。原因参考https://zhuanlan.zhihu.com/p/50168473(但是对博客中的解释感觉有点莫名其妙。。)
x ^ ← ϵ x + ( 1 − ϵ ) x ~ \hat{\boldsymbol{x}} \leftarrow \epsilon \boldsymbol{x}+(1-\epsilon) \tilde{\boldsymbol{x}} x^←ϵx+(1−ϵ)x~
在inpainting任务中,与GAN不同的是,我们只深层特定区域,即待修复区域(输入中用mask标记了的部门),因此这部分限制变为(m为mask)
λ E x ^ ∼ P x ^ ( ∥ ∇ x ^ D ( x ^ ) ⊙ ( 1 − m ) ∥ 2 − 1 ) 2 \lambda E_{\hat{\mathbf{x}} \sim \mathbb{P}_{\hat{\mathbf{x}}}}\left(\left\|\nabla_{\hat{\mathbf{x}}} D(\hat{\mathbf{x}}) \odot(\mathbf{1}-\mathbf{m})\right\|_{2}-1\right)^{2} λEx^∼Px^(∥∇x^D(x^)⊙(1−m)∥2−1)2
小结
和上一篇(High-Resolution Image Inpainting using Multi-Scale Neural Patch Synthesis(CVPR2017))一样,先通过网络脑补出一个粗略的修补图,在用这个修补图去和已知区域匹配refine。只是上一篇是求L2距离最近的background,然后最小化这个L2优化。而这是用cosine距离求最相似的,然后做deconvolution。
同时不在限制生成区域的大小和位置和数量。
另外输入加个mask就能指示网络去学习指定位置了吗?
