Recurrent Neural Network - 从零开始实现循环神经网络(RNN循环神经网络)

核心概念

循环神经网络与多层感知机网络的核心区别是: 有无隐状态。

隐状态是记录时间序列的参数，即上个时间的结果信息，有利于处理和预测序列数据。如股价预测、有逻辑的一段话等。所以也常应用于NLP领域。

---

无隐状态的神经网络(如多层感知机MLP):

$$\mathbf{H}=\varphi (\mathbf{X}{\mathbf{W}}_{xh}+{\mathbf{b}}_h).$$

输出为:

$$O=H{W}_{hq}+b_q$$

其中，$\varphi$代表激活函数，$W_{xh}$代表权重矩阵，$b_h$代表偏置, $O$代表输出。

---

有隐状态的神经网络(即循环神经网络RNN):

$${\mathbf{H}}_t=\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}+{\mathbf{b}}_h).$$

输出为:

$$O_t=H_t{W}_{hq}+b_q$$

其中，添加了 $H_{t-1}$ 代表上个时序隐状态，$W_{hh}$ 代表了其对应的权重矩阵, $O_t$代表时间段t的输出。

故根据上述公式即可构建RNN循环神经网络。

---

Step1: 加载数据集

引入必要的依赖包

import math
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

加载数据集time_mechine(train_iter的范围为(1~27))，不清楚的朋友可以自行搜索了解。

#定义数据批量大小为 32， 时间步数为 35， 即迭代器train_iter内的X, y的形状均为(32, 35), vocab为词表
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

Step2: 独热编码(one-hot编码)

回想一下，之前在train_iter中，每个词元都表示为一个数字索引， 将这些索引直接输入神经网络可能会使学习变得困难。 我们通常将每个词元表示为更具表现力的特征向量。 最简单的表示称为独热编码（one-hot encoding）。

如下图，索引0和2的编码如下所示:

F.one_hot(torch.tensor([0, 2]), len(vocab))

tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 0],
        [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 0]])

现在对X数据集进行独热编码，它可以有三个维度，分别为: (时间步数，批量大小，词表大小)。

X = torch.arange(10).reshape((2, 5))
F.one_hot(X.T, 28).shape                #该三个维度分别为(时间步数，批量大小，词表大小)

torch.Size([5, 2, 28])

Step3: 初始化模型参数

接下来，我们初始化循环神经网络模型的模型参数。 隐藏单元数num_hiddens是一个可调的超参数。 当训练语言模型时，输入和输出来自相同的词表。 因此，它们具有相同的维度，即词表的大小。

def get_params(vocab_size, num_hiddens, device):
    
    #词表的大小，输入大小，输出大小相同
    num_inputs = num_outputs = vocab_size
    
    #生成初始化分布值
    def normal(shape):
        return torch.randn(size=shape, device=device) * 0.01
    
    #隐藏层参数
    W_xh = normal((num_inputs, num_hiddens))                 #输入时的权重
    W_hh = normal((num_hiddens, num_hiddens))                #序列记忆的权重
    b_h = torch.zeros(num_hiddens, device=device)            #偏置量
    
    #输出层参数
    W_hq = normal((num_hiddens, num_outputs))                #输出时的权重
    b_q = torch.zeros(num_outputs, device=device)            #输出的偏置量
    
    #附加梯度
    params = [W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    
    #返回参数
    return params
    

Step4: 循环神经网络模型

为了定义循环神经网络模型， 我们首先需要一个init_rnn_state函数在初始化时返回隐状态。这个函数的返回是一个张量，张量全用0填充，形状为（批量大小，隐藏单元数）。

#初始化rnn循环神经网络的隐状态
def init_rnn_state(batch_size, num_hiddens, device):
    #返回一个记忆状态信息
    return (torch.zeros((batch_size, num_hiddens), device=device), )

下面的rnn函数定义了如何在一个时间步内计算隐状态和输出。循环神经网络模型通过inputs最外层的维度实现循环，以便逐时间步更新小批量数据的隐状态 H。 此外，这里使用 $ \tanh $ 函数作为激活函数。

#前向传播函数，并计算状态值 H
def rnn(inputs, state, params):
    
    #inputs的形状: (时间步数量，批量大小，词表大小)
    W_xh, W_hh, b_h, W_hq, b_q = params
    
    H, = state                                            #记忆状态
    outputs = []                                          #初始化输出列表
    
    #X的形状: (批量大小，词表大小)
    for X in inputs:
        H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)        #计算结果记忆H
        Y = torch.mm(H, W_hq) + b_q                                        #计算输出结果Y
        outputs.append(Y)                                 #追加 结果Y 至 output输出中
    
    return torch.cat(outputs, dim=0), (H, )                                #返回记忆H与结果Y

定义了所有需要的函数之后，接下来我们创建一个类来包装这些函数，并存储从零开始实现的循环神经网络模型的参数。

class RNNModelScratch:
    
    """从零开始实现的循环神经网络模型"""
    def __init__(self, vocab_size, num_hiddens, device, get_params, 
                init_state, forward_in):
        
        #定义词表大小，隐单元个数
        self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
        
        #定义参数
        self.params = get_params(vocab_size, num_hiddens, device)
        
        #定义初始化隐状态，前向传播函数
        self.init_state, self.forward_in = init_state, forward_in
        
    def __call__(self, X, state):
        X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
        return self.forward_in(X, state, self.params)
    
    def begin_state(self, batch_size, device):
        return self.init_state(batch_size, self.num_hiddens, device)

让我们检查输出是否具有正确的形状。 例如，隐状态的维数是否保持不变。

num_hiddens = 512                               #定义隐单元个数512

#定义网络
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
                     init_rnn_state, rnn)

#初始化记忆隐状态
state = net.begin_state(X.shape[0], d2l.try_gpu())

d2l.try_gpu()
# #返回Y的值和状态state的值
Y, new_state = net(X.to(d2l.try_gpu()), state)

Y.shape, len(new_state), new_state[0].shape

(torch.Size([10, 28]), 1, torch.Size([2, 512]))

我们可以看到输出形状是（时间步数 $ \times $ 批量大小，词表大小）， 而隐状态形状保持不变，即（批量大小，隐藏单元数）。

Step5: 预测

让我们首先定义预测函数来生成prefix之后的新字符， 其中的prefix是一个用户提供的包含多个字符的字符串。 在循环遍历prefix中的开始字符时， 我们不断地将隐状态传递到下一个时间步，但是不生成任何输出。 这被称为预热（warm-up）期， 因为在此期间模型会自我更新（例如，更新隐状态）， 但不会进行预测。 预热期结束后，隐状态的值通常比刚开始的初始值更适合预测， 从而预测字符并输出它们。

def predict_ch8(prefix, num_preds, net, vocab, device):
    
    """在prefix后面生成新字符"""
    #生成最初的隐状态数据，形状为(1, 512)
    state = net.begin_state(batch_size=1, device=device)
    
    #首先获取第一个字母对应的字典idx，初始化输出列表
    outputs = [vocab[prefix[0]]]
    
    #初始化输入列表，输入数据为输出列表的最后一个数据
    get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
    
    #预热期
    for y in prefix[1:]:
        _, state = net(get_input(), state)                 #记录当前的隐状态
        outputs.append(vocab[y])                          #输出集合追加y在字典中的索引
    
    #预测num_preds步
    for _ in range(num_preds):
        y, state = net(get_input(), state)                           #进行预测操作，返回预测得到的结果及隐状态
        outputs.append(int(y.argmax(dim=1).reshape(1)))              #追加预测所得结果new_y至输出列表中
            
    return ''.join([vocab.idx_to_token[i] for i in outputs])         #输出预测所得的新数据

现在我们可以测试predict_ch8函数。 我们将前缀指定为time traveller， 并基于这个前缀生成10个后续字符。 鉴于我们还没有训练网络，它会生成荒谬的预测结果。

predict_ch8('time traveller ', 10, net, vocab, d2l.try_gpu())

'time traveller ysprrxcgpr'

Step6: 梯度裁剪

主要公式:

$$g\leftarrow min(1,\frac{\theta }{||g||})g$$

目的: 控制梯度的范围，当梯度过大时，为防止梯度爆炸，对梯度进行裁剪操作。

def grad_clipping(net, theta):
    """裁剪梯度"""
    #首先获取神经网络中的参数
    if isinstance(net, nn.Module):
        params = [p for p in net.parameters() if p.requires_grad]
    else:
        params = net.params
    
    #计算参数梯度的第二范式
    norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
    
    #若norm > theta， 则对网络的所有参数进行梯度裁剪
    if norm > theta:
        for param in params:
            param.grad[:] *= theta / norm

Step7: 训练

在训练模型之前，让我们定义一个函数在一个迭代周期内训练模型。

1.序列数据的不同采样方法 （随机采样和顺序分区） 将导致隐状态初始化的差异。

2.我们在更新模型参数之前裁剪梯度。 这样的操作的目的是：即使训练过程中某个点上发生了梯度爆炸，也能保证模型不会发散。

3.我们用困惑度来评价模型，这样的度量确保了不同长度的序列具有可比性。

def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):
    """训练网络一个迭代的周期"""
    state, timer = None, d2l.Timer()            #定义初始化状态，时间类
    metric = d2l.Accumulator(2)                 #训练损失之和， 词元数量
    
    for X, Y in train_iter:
        if state is None or use_random_iter:
            #在第一次迭代或使用随机抽样时初始化state(32, 512)
            state = net.begin_state(batch_size=X.shape[0], device=device)
        else:
            if isinstance(net, nn.Module) and not isinstance(state, tuple):
                #state 对于 nn.GRU 是个张量
                state.detach_()
            
            else:
                #state对于nn.LSTM或对于我们从零开始实现的模型是个张量
                for s in state:
                    s.detach_()
    
        y = Y.T.reshape(-1)                               #将y展开为一维数组
        X, y = X.to(device), y.to(device)                 #把x，y放入选定设备中
        y_hat, state = net(X, state)                      #预测y_hat(1120,28)以及记忆state(32,512)
        l = loss(y_hat, y.long()).mean()                  #计算损失值

        if isinstance(updater, torch.optim.Optimizer):    #torch包内的优化器
            updater.zero_grad()                           #清空梯度
            l.backward()                                  #反向传播函数
            grad_clipping(net, 1)                         #梯度裁剪
            updater.step()                                #更新参数
        else:
            l.backward()                                  #自定义的优化器
            grad_clipping(net, 1)                         #梯度裁剪
            # 因为已经调用了mean函数
            updater(batch_size=1)                         #更新梯度

        metric.add(l * y.numel(), y.numel())              #累计损失值与样本数量

    #返回平均损失与训练时长
    return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()
    
    

循环神经网络模型的训练函数既支持从零开始实现， 也可以使用高级API来实现。

#定义RNN循环神经网络的训练函数
def train_ch8(net, train_iter, vocab, lr, num_epochs, device,
             use_random_iter=False):
    
    """训练模型"""
    loss = nn.CrossEntropyLoss()                                #定义交叉熵损失函数
    
    animator = d2l.Animator(xlabel='epoch', ylabel='proplexity',
                           legend=['train'], xlim=[10, num_epochs])
    
    #初始化，定义优化函数
    if isinstance(net, nn.Module):
        updater = torch.optim.SGD(net.parameters(), lr)
    else:
        updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
        
    predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device)
    
    #训练和预测
    for epoch in range(num_epochs):
        #训练模型，获取平均损失以及训练速度
        ppl, speed = train_epoch_ch8(
            net, train_iter, loss, updater, device, use_random_iter)
        
        #每迭代十次后，绘图
        if (epoch + 1) % 10 == 0:
            print(predict('time traverller'))
            animator.add(epoch+1, [ppl])
    
    print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
    print(predict('time traveller'))
    print(predict('traveller'))

现在，我们训练循环神经网络模型。 因为我们在数据集中只使用了10000个词元， 所以模型需要更多的迭代周期来更好地收敛。

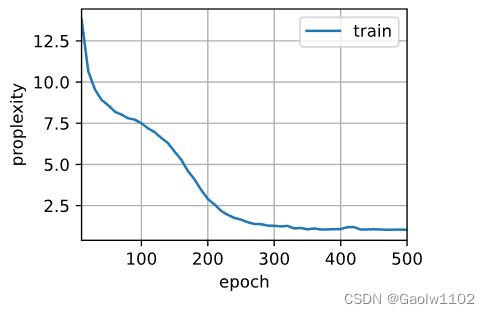
num_epochs, lr = 500, 1
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu())

困惑度 1.0, 10062.6 词元/秒 cpu
time traveller for so it will be convenient to speak of himwas e
travelleryou can show black is white by argument said filby

最后，让我们检查一下使用随机抽样方法的结果。

net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
                      init_rnn_state, rnn)
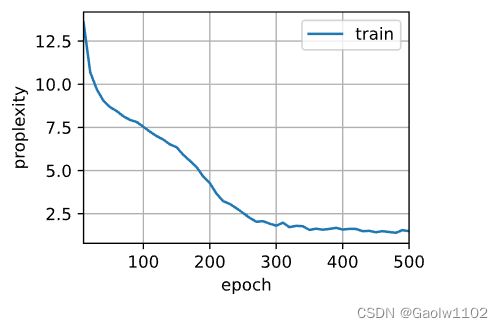
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(),
          use_random_iter=True)

困惑度 1.5, 10250.9 词元/秒 cpu
time travelleryou can show bat s four ho taf at alway about this
travelleryou can show bat s four ho taf at alway about this

从零开始实现上述循环神经网络模型， 虽然有指导意义，但是并不方便。 下次，我们将学习如何改进循环神经网络模型。 例如，如何使其实现地更容易，且运行速度更快。

小结

1.我们可以训练一个基于循环神经网络的字符级语言模型，根据用户提供的文本的前缀生成后续文本。

2.一个简单的循环神经网络语言模型包括输入编码、循环神经网络模型和输出生成。

3.循环神经网络模型在训练以前需要初始化状态，不过随机抽样和顺序划分使用初始化方法不同。

4.当使用顺序划分时，我们需要分离梯度以减少计算量。

5.在进行任何预测之前，模型通过预热期进行自我更新（例如，获得比初始值更好的隐状态）。

6.梯度裁剪可以防止梯度爆炸，但不能应对梯度消失。