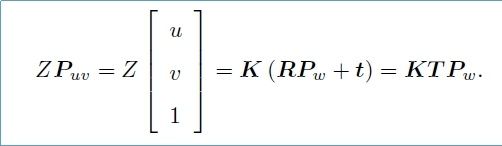SLAM学习笔记----坐标关系梳理及PnP算法详解

一，重要的坐标关系的解析

四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。

世界坐标系：机器人或相机运动过程中，肯定需要知道它的位置，因此需要设定世界坐标系，认定固定不动，作为 参考坐标系，描述世界中的任何一点P（Xw,Yw,Zw)。

相机坐标系：相机或机器人运动的一个坐标系，通过世界坐标系的变换（旋转R,平移T）计算得到。因此主要是将 世界坐标系描述的点坐标P（Xw,Yw,Zw)转换成相机坐标系下描述P（Xc,Yc,Zc)，方便计算得到在成像坐标系的坐 标。

图像（成像）坐标系：描述点在图像坐标系的成像点位置。

像素坐标：在相机中得到的是一个像素，因此主要将图像坐标系的点转换成像素坐标系下。

1.1 世界坐标到相机坐标

两者的关系是旋转和平移的关系：

其中旋转矩阵的含义：

1.2 从相机坐标系与图像坐标系

从相机坐标系到图像坐标系，属于透视投影关系，从3D转换到2D。此时P点已由上面经过世界坐标系转换成相机坐标系下表述P(Xc,Yc,Zc)，接下来需要将相机坐标转换到图像坐标，这时候强依赖的是相机的内参：

1.3 图像坐标系与像素坐标系

        像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成 像平面的交点，通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下：其中dx和dy 表示每一列和每一行分别代表多少mm，即1pixel=dx mm .

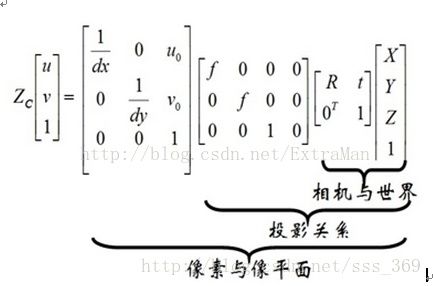
1.4 一个点从世界坐标系如何转换到像素坐标系

使用相机的内外参表示从世界坐标系到像素坐标系的关系，可以使用如下的式子：

 K表示相机内参，T表示相机外参，公式可以简化为如下的式子：

      其中相机的内参和外参可以通过张正友标定获取（戳这里查看张正友标定的资料）。通过最终的转换关系来看，一个三维中的坐标点，的确可以在图像中找到一个对应的像素点，但是反过来，通过图像中的一个点找到它在三维中 对应的点就很成了一个问题，因为我们并不知道等式左边的Zc的值。 

相关坐标关系，讲的较为明确的可以参考以下链接：

SLAM基础知识总结_Arrow的博客-CSDN博客

二、什么是PnP

    PnP为 Perspective-n-Point的简称，是求解3D到2D点对的运动的方法:即给出n个3D空间点时，如何求解相机的位姿。直白的翻译就是：PNP 相机位姿估计pose estimation就是通过几个已知坐标(世界坐标)的特征点,结合他们在相机照片中的成像(像素坐标),求解出相机所在的世界坐标以及旋转角度(这两个货叫相机的外参), 用旋转矩阵(R)和平移矩阵(t)表示. 这个算法的输入是一组点的三维世界坐标和二维像素坐标,输出是相机的旋转矩阵(R)和平移矩阵(t). OpenCV有相应的库函数solvePnP()和solvePnPRansac(),后者利用了ransac的思想计算更加精确的结果,不过据说速度很慢,完全没法做到实时.

     2D-2D对极几何如何确定相机姿态。2D-2D是通过两张由单目相机拍摄的平面图，通过三角化确定特征点的深度，通过两张图片相机位置的图像转换而确定相机运动R,T。而3D-2D是已知其中一张照片的深度和另一张照片的像素坐标求相机姿态R，T。

特征点的3D位置可以由三角化(相机是单目)或RGB-D相机的深度图确定。所以在双目或RGB-D的视觉里程计中，我们可以直接使用PnP估计相机运动。而单目视觉里程计中，必须先进行初始化，然后才能使用PnP。 

 2.1 PnP常用的求解方法

2.1.1 P3P

     P3P该方法并不直接求解运动，而是通过求解特征点的世界坐标的相机坐标，把2D-3D问题转换为3D-3D问题，然后再使用ICP求解。即将（2D-3D）-------转换----（3D-3D）-------使用ICP求相机的运动。

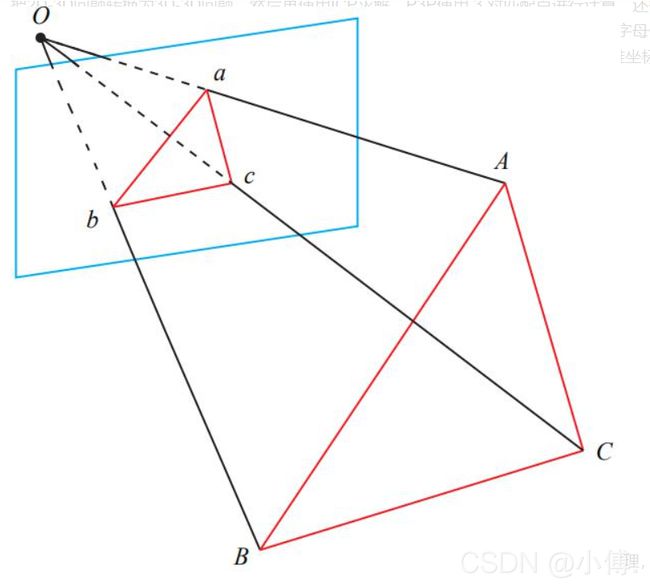
      P3P使用 3 对匹配点进行计算，还需要一对验证点D−d，从可能的解中选出正确的。记 3D 点为A, B, C，2D 点为 a, b, c，其中小写字母代表的点为对应大写字母代表的点在相机成像平面上的投影。注意，A, B, C 在世界坐标系中的3维坐标，而不是在相机坐标系。一旦3D点在相机坐标系下的坐标能够计算出来，我们就得到3D-3D的对应的，就可以转换为ICP的问题。如下：

      相似三角形公式， 记 v = AB2/OC2, u = BC2/AB2, w = AC2/AB2,则uv = BC2/OC2, wv = AC2/OC2，有：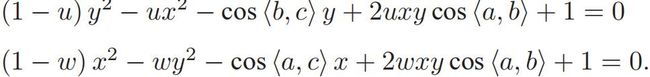

 其中： x=OA/OC, y=OB/OC

       已经知道2D 点的图像位置，则3个余弦角 cos〈a, b〉, cos〈b, c〉, cos〈a, c〉是已知的，u,w可以通过 A,B,C 在世界坐标系下的坐标算出。剩下的 x, y 是未知的，随着相机移动会发生变化。因此，该方程组是关于 x, y 的一个二元二次方程（多项式方程）。解析地求解该方程组是一个复杂的过程，需要用吴消元法。

    该方程最多可能得到 4 个解，可以用验证点来计算最可能的解，得到 A, B, C在相机坐标系下的 3D 坐标。然后，根据 3D−3D 的点对，使用ICP（迭代最近点）计算相机的运动 R, t。
    存在的问题：

1. P3P 只利用 3 个点的信息。当给定的配对点多于 3 组时，难以利用更多的信息。

2. 如果 3D 点或 2D 点受噪声影响，或者存在误匹配，则算法失效。
 

2.1.2 直接线性变换

 求解相机的外参：R、t透视投影模型为：

每组3D-2D匹配点对应两个方程，一共有12个未知数，至少需要6组匹配点。设有N组匹配点，则：

上式写成矩阵形式：AF=0，当N=6时，可以直接求解线性方程组。

因此, 旋转矩阵, 平移矩阵求得:

2.1.3 BA

PnP是通过一组匹配好的3D点和2D点来求解两帧图像之间运动的一种算法。PNP的求解有DLT(直接线性变换)、P3P、EPNP和BA优化等方式。

ICP的求解有两种方式：线性代数的求解(SVD),非线性优化方式(BA).

基于图的SLAM算法里面使用图优化替代了原来的滤波器，这里图优化就是指BA。

BA的定义： 从视觉重建中提炼出最优的3D模型和相机参数，从每个特征点反射出来的几束光线，把相机姿态和特征点空间位置做出最优调整之后，最后收束到相机光心的过程简称BA。它在视觉SLAM中起核心作用。

BA本质上就是最小化重投影残差同时优化位姿和路标点，以便从每个特征点反射出的光线通过调整最后都能通过相机光心，因此也称捆集优化或光束平差法。
 

SLAM中的BA优化，先根据相机模型和A,B图像特征匹配好的像素坐标，求出A图像上的像素坐标对应的归一化的空间点坐标，然后根据该空间点的坐标计算重投影到B图像上的像素坐标，重投影的像素坐标(估计值)与匹配好的B图像上的像素坐标(测量值),不会完全重合，BA的目的就是每一个匹配好的特征点建立方程，然后联立，形成超定方程，解出最优的位姿矩阵或空间点坐标(两者可以同时优化)。反向求解，使得相机模型正确让误差最小。

详细的推导过程详见以下博文：

SLAM中的BA优化_爱宝宝的菜鸟的博客-CSDN博客_ba优化

 2.1.4 SLAM常用到的工具库

开发SLAM常用到的工具库主要包括：
OpenNI：用于与视觉传感器的交互操作；
OpenCV：用于图像处理；
PCL：用于点云处理；
Eigen：用于矩阵运算；
Sophus：用于李群李代数计算；
Ceres Solver：用于非线性优化；
g2o：用于图优化；
DBoW：用于处理词袋模型；
OpenGL：用于模型渲染；
CUDA toolkit：用于并行计算，等等。 

3.总结