《图解深度学习》学习笔记(四)
第5章 自编码器
自编码器是一种基于无监督学习的数据维度压缩和特征表达方法,多层自编码器能够更好地进行压缩及特征表达。
自编码器有多种变种:降噪自编码器、稀疏自编码器、以及由多层自编码器组成的栈式自编码器。
一、自编码器
自编码器是一种有效的数据维度压缩算法,主要应用于一下两个方面。
- 构建一种能够重构输入样本并进行特征表达的神经网络。
- 训练多层神经网络时,通过自编码器训练样本得到参数初始值。
“特征表达”是指对于分类会发生变动的不稳定模式,例如手写字符识别中由于不同人的书写习惯和风格的不同造成字符模式不稳定,或者输入样本中包含噪声等情况,神经网络也能将其转换成可以准确识别的特征。当样本中包含噪声时,如果神经网络能够消除噪声,则被称为降噪自编码器(denoising autoencoder)。另外还有一种称为稀疏自编码器(sparse autoencoder)的网络,它在自编码器中引入了正则化项,以去除冗余信息。
“得到参数初始值”是指在多层神经网络中得到最优参数。一个多层神经网络的训练,首先要利用随机数初始化训练样本的参数,然后通过训练样本得到最优参数。但是,如果是层数较多的神经网络,即使使用误差反向传播算法也很难把误差梯度有效反馈到底层,这样就会导致神经网络训练困难。所以,需要使用自编码器计算每层的参数,并将其作为神经网络的参数初始值逐层训练,以便得到更加完善的神经网络模型。
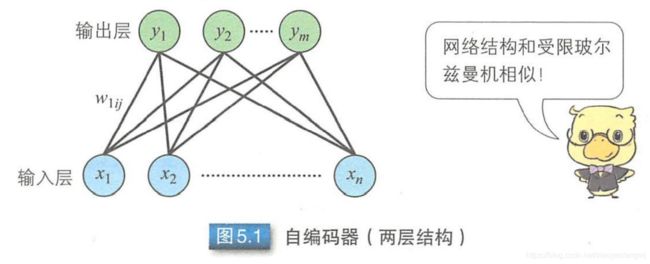
自编码器和受限玻尔兹曼机一样都是两层结构,有输入层和输出层组成。图中输入数据x与对应的连接权重W相乘,再加上偏置b,并经过编码器激活函数f(.)变换后,就可以得到输出y。y = f(Wx+b)。
自编码器是一种基于无监督学习的神经网络,目的在于通过不断调整参数,重构经过维度压缩的输入样本。如下图5.2。重构输入样本的三层神经网络。输入层到中间层之间的映射称为编码,把中间层到输出层之间的映射称为解码。
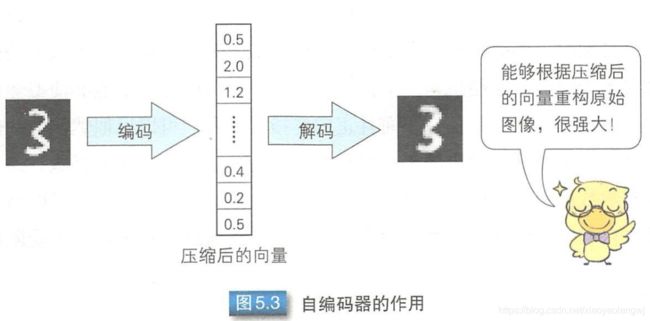
编码和解码过程如图5.3所示,先通过编码得到压缩后的向量,再通过解码进行重构。
中间层和重构层之间的连接权重及偏置分别记作![]()
![]() 和
和![]() ,重构值(解码结果)记作
,重构值(解码结果)记作![]() 。
。![]() 。
。![]() 表示解码器的激活函数。
表示解码器的激活函数。
自编码器的训练就是确定编码器和解码器的参数W和b,![]()
![]() 和
和![]() 的过程。首先使用公式
的过程。首先使用公式![]() 计算输入样本x的重构值
计算输入样本x的重构值![]() ,然后使用误差反向传播算法调整参数值,不断迭代上述过程直至误差函数收敛于极小值。误差函数可以使用最小二乘法函数或者交叉熵代价函数。
,然后使用误差反向传播算法调整参数值,不断迭代上述过程直至误差函数收敛于极小值。误差函数可以使用最小二乘法函数或者交叉熵代价函数。
上面说的编码器的连接权重W和解码器的连接权重![]() ,两者数值不同。不过编码器和解码器可以共享连接权重,这称为权重共享,可以用公式表示
,两者数值不同。不过编码器和解码器可以共享连接权重,这称为权重共享,可以用公式表示![]() =W。
=W。
自编码器和受限玻尔兹曼机的结构相似,都是两层。两者最大的区别在于受限玻尔兹曼机是一个概率模型,训练目的是求出能够使似然函数达到极大值的参数估计,而且正向传播时,我们可以以似然函数的值为概率决定单元的输出结果。而自编码器需要定义一个误差函数,通过调整参数使得输入样本和重构结果的误差收敛于极小值。和神经网络一样,自编码器的计算结果也会进行正向传播,这就是自编码器和受限玻尔兹曼机的主要区别。
二、降噪自编码器
自编码器的重构结果和输入样本的模式是相同的。在自编码器的基础上衍生的降噪自编码器如图5.4所示。
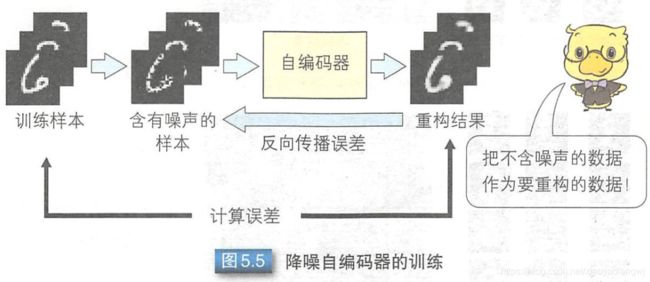
降噪自编码器的网络结构与自编码器一样,只是对训练方法进行了改进,改进后的训练过程如图5.5所示。
把干净样本加入噪声作为训练集,然后重构结果与干净样本做参照,使其误差最小,这样训练出来的模型,就具有了降噪能力。
自编码器是把训练样本直接输入给输入层,而降噪自编码器则是把通过向训练样本中加入随机噪声得到的样本![]() 输入给输入层。
输入给输入层。![]() (自加噪声造数据)。随机噪声v服从均值为0、方差为
(自加噪声造数据)。随机噪声v服从均值为0、方差为![]() 的正态分布。我们需要训练神经网络,使得重构结果与不含噪声的样本之间的误差收敛于极小值。误差函数会对不含噪声的输入样本进行测试,故降噪自编码器能够完成下述两项训练。
的正态分布。我们需要训练神经网络,使得重构结果与不含噪声的样本之间的误差收敛于极小值。误差函数会对不含噪声的输入样本进行测试,故降噪自编码器能够完成下述两项训练。
- 保持输入样本不变的条件下,提取能够更好地反映样本属性的特征。
- 消除输入样本中包含的噪声。
图5.6为一个降噪自编码器的训练示例。输入样本使用的是MNIST手写字符识别数据集,样本图像大小为28*28。神经网络的输入层有28*28=784个单元,中间层有100个单元,重构层有784个单元,与输入层相等。图5.6用可视化的形式表示了中间层100个单元之间的连接权重,可见训练后的连接权重能够捕获到手写字符的边缘。另外,与原始输入样本比起来,自编码器的重构结果图像相对模糊。图像(b)和图像(c)是分别向输入样本中添加了20%和40%噪声后的重构结果。添加噪声会导致部分字符丢失,但是在将含有噪声的图像作为输入样本重构原始输入时,得到的结果和不含噪声时相差无几。
三、稀疏自编码器
自编码器是一种有效的数据维度压缩算法。它会对神经网络的参数进行训练,使输出层尽可能如实地重构输入样本。但是中间层的单元个数太少会导致神经网络很难重构输入样本,而单元个数太多又会产生单元冗余,降低压缩效率。为了解决这个问题,人们将稀疏正则化引入到自编码器中,提出了稀疏自编码器。通过增加正则化项,大部分单元的输出都变为了0,这样就能利用少数单元有效完成压缩或重构。加入正则化项后的误差函数E:
偷懒了:实在整理不动公式了。这里面有个KL散度需要进一步学习了解。
四、栈式自编码器
自编码器、降噪自编码器以及稀疏自编码器都是包括编码器和解码器的三层结构,但是在进行维度压缩时,可以只包括输入层和中间层。把输入层和中间层多层堆叠后,就可以得到栈式自编码器(Stacked autocoder)。栈式自编码器和深度信念网络一样,都是逐层训练,从第二层开始,前一个自编码器的输出作为后一个自编码器的输入。但是两种网络的训练方法不同。深度信念网络是利用对比散度算法逐层训练两层之间的参数。而栈式自编码器的训练则如图5.8所示,首先训练第一个自编码器,然后保留第一个自编码器的编码部分,并把第一个自编码器的中间层作为第二个自编码器的输入层进行训练,后续过程就是反复地把前一个自编码器的中间层作为后一个编码器的输入层,进行迭代训练。通过多层堆叠,栈式自编码器能够有效地完成输入模式的压缩。以手写字符为例,第一层自编码器嫩够捕捉到部分字符,第二层自编码器能够捕捉部分字符的组合,更上层的自编码器能够捕捉进一步的组合。这样就能逐层完成低维到高维的特征提取。
五、在预训练中的应用
栈式自编码器和多层神经网络都能得到有效的参数,所以我们可以把训练后的参数作为神经网络或卷积神经网络的参数初始值,这种方法叫做预训练。首先,选取多层神经网络的输入层和第一个中间层,组成一个自编码器,然后先进行正向传播,再进行反向传播,计算输入与重构结果的误差,调整参数从而使误差收敛于极小值。接下来,训练输入层与第一个中间层的参数,把正向传播的值作为输入,训练其与第二个中间层之间的参数。然后调整参数,使第一个中间层的值与第二个中间层反向传播的值之间的误差收敛于极小值。这样,对第一个中间层的值得重构就完成了。对网络的所有层进行预训练后,可以得到神经网络的参数初始值。截止目前,我们一直使用的是无监督学习,接下来需要使用有监督学习来调整整个网络的参数,这也叫作微调(fine tuning)。如果不实施预训练,而是使用随机数初始化网络参数,网络训练可能会无法顺利完成。实施预训练后,可以得到能够更好地表达训练对象的参数,得到训练过程更加顺利。
六、小结
自编码器有多种用途,不仅可以作为无监督学习的特征提取器,还可以用于降噪以及神经网络和卷积神经网络的参数初始值预训练。网络训练使用的也是误差反向传播算法。