ccc-机器学习算法基础-5
线性回归
1.基本简介
线性回归是回归分析的一种。构造步骤为:
- 假设因变量与自变量之间线性相关
- 构建损失函数
- 通过令损失函数最小来确定参数
- 通用公式: h ( w ) = w 0 + w 1 x 1 + w 2 x 2 + … = w T x ℎ(w)= w_0+w_1x_1+w_2x_2+…= w^Tx h(w)=w0+w1x1+w2x2+…=wTx其中 w , x w,x w,x为矩阵
2.损失函数(最小二乘法)
误差平方和:
j ( θ ) = ( h w ( x 1 ) − y 1 ) 2 + ( h w ( x 2 ) − y 2 ) 2 + ⋯ + ( h w ( x m ) − y m ) 2 = ∑ i = i m ( h w ( x i ) − y i ) 2 j(\theta)=(h_w(x_1)-y_1)^2+(h_w(x_2)-y_2)^2+\cdots+(h_w(x_m)-y_m)^2=\sum_{i=i}^{m}(h_w(x_i)-y_i)^2 j(θ)=(hw(x1)−y1)2+(hw(x2)−y2)2+⋯+(hw(xm)−ym)2=i=i∑m(hw(xi)−yi)2
梯度下降(理解过程):
沿着函数下降的方向找,最后就能找到山谷的最低点,然后更新W值
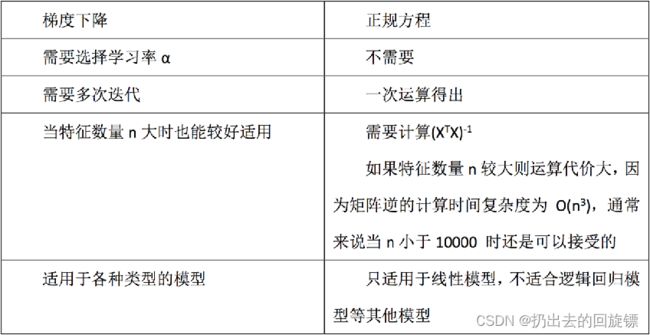
3.正规方程API
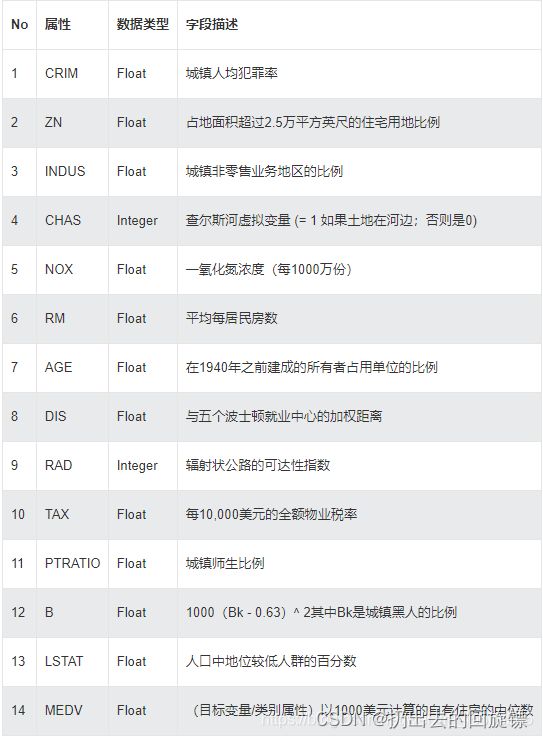
波士顿房价预测:
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def linear():
lb = load_boston()
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 由于x y的特征个数不同,要分别标准化
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# 正规方程求解
lr = LinearRegression()
lr.fit(x_train,y_train)
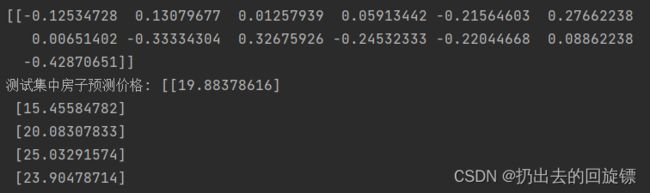
print(lr.coef_)
# 将标准化后的数据转换为原始数据
y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
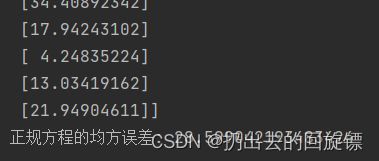
print("测试集中房子预测价格:",y_lr_predict)
print("正规方程的均方误差:",mean_squared_error(std_y.inverse_transform(y_test),y_lr_predict))
return None
if __name__ == '__main__':
linear()
说明:
- LinearRegression 参数
4.梯度下降 API(红酒口感)
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
data = np.genfromtxt('winequality-red.csv',delimiter=';',skip_header=True)
X = data[:,:-1]
y = data[:,-1]
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
#将数据进行标准化处理
ss = StandardScaler()
ss.fit(X_train)
X_train_std = ss.transform(X_train)
X_test_std = ss.transform(X_test)
#训练模型
sgd=SGDRegressor()
sgd.fit(X_train_std,y_train)
y_pred = sgd.predict(X_test_std)
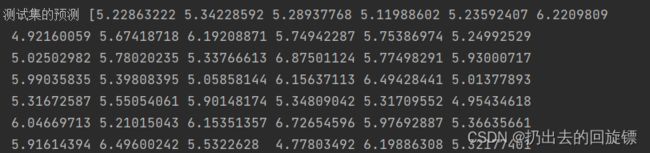
print('测试集的预测',y_pred)
mse = mean_squared_error(y_test,y_pred)
print('梯度下降的均方误差:',mse)
说明:
5.过拟合与欠拟合
过拟合:
概念:一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在训练数据外的数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
过拟合原因:
原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决方式:
- 进行特征选择,消除关联性大的特征(很难做)
- 交叉验证(让所有数据都有过训练)
- 正则化(减少高阶的权重)
欠拟合:
概念:一个假设在训练数据上不能获得更好的拟合, 但是在训练数据外的数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
欠拟合原因:
学习到数据的特征过少
解决方式:
增加数据的特征数量

6.岭回归 API(带正则化的回归)
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression,Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def linear():
lb = load_boston()
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 由于x y的特征个数不同,要分别标准化
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# 岭回归预测
rd = sgd = Ridge(alpha=1.0)
rd.fit(x_train,y_train)
print(rd.coef_)
y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
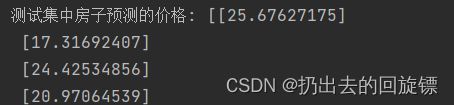
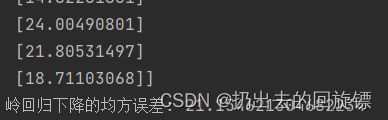
print("测试集中房子预测的价格:",y_rd_predict)
print("岭回归下降的均方误差:",mean_squared_error(std_y.inverse_transform(y_test),y_rd_predict))
return None
if __name__ == '__main__':
linear()