【吴恩达机器学习笔记】第五章 神经网络学习
【吴恩达机器学习笔记】第五章 神经网络学习
1、神经网络模型
我们将一个神经元模拟成一个逻辑单元,下图表示对 h θ ( x ) h_{\theta }(x) hθ(x) 进行计算的神经元,黄色圆圈代表一个神经元,蓝色圆圈代表树突或轴突传输的信号。

假设 h θ ( x ) h_{\theta }(x) hθ(x) 是logistic函数,则这个神经元也可以被称为一个带有logistic激活函数的人工神经元。
在神经网络术语中,激活函数是指非线性函数 g ( z ) g(z) g(z) 的另一个术语。在神经网络的文献中, θ \theta θ 参数有时也被称为权重。
神经网络其实是一组神经元连接在一起的组合,如下图所示:
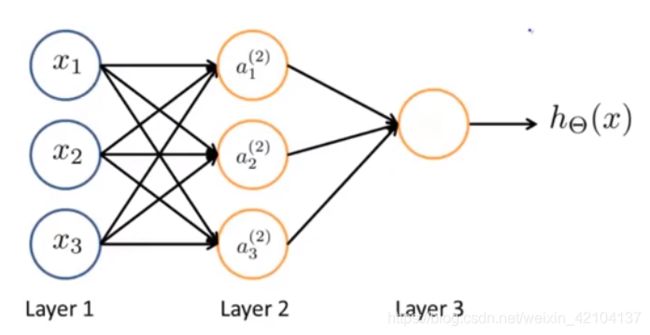
神经网络术语中,第一层也被称为输入层,因为我们在这一层输入特征,最后一层也被成为输出层,因为这一层的神经元输出假设的最终计算结果,中间第二层被称为隐藏层。
为了解释神经网络的计算过程,首先我们需要记住以下符号
a i ( j ) a_{i}^{(j)} ai(j) :表示第 j j j 层第 i i i 个神经元或单元的激活项,激活项是指由一个具体神经元计算并输出的值。
Θ ( j ) \Theta ^{(j)} Θ(j) :表示权重矩阵。它控制从某一层到下一层的映射。如果一个网络在第 j j j 层有 s j s_{j} sj 个单元,在第 j + 1 j+1 j+1 层有 s j + 1 s_{j+1} sj+1 个单元,那么矩阵 Θ ( j ) \Theta ^{(j)} Θ(j) 即控制第 j j j 层到第 j + 1 j+1 j+1 层映射的矩阵。它的维度为 s j + 1 × ( s j + 1 ) s_{j+1}\times (s_j+1) sj+1×(sj+1)
上图的的神经网路所表示的计算如下所示:
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_{1}^{(2)}=g(\Theta _{10}^{(1)}x_{0}+\Theta _{11}^{(1)}x_{1}+\Theta _{12}^{(1)}x_{2}+\Theta _{13}^{(1)}x_{3}) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_{2}^{(2)}=g(\Theta _{20}^{(1)}x_{0}+\Theta _{21}^{(1)}x_{1}+\Theta _{22}^{(1)}x_{2}+\Theta _{23}^{(1)}x_{3}) a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_{3}^{(2)}=g(\Theta _{30}^{(1)}x_{0}+\Theta _{31}^{(1)}x_{1}+\Theta _{32}^{(1)}x_{2}+\Theta _{33}^{(1)}x_{3}) a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
h Θ ( x ) = a 1 ( 3 ) = g ( Θ 10 ( 1 ) a 0 ( 2 ) + Θ 11 ( 1 ) a 1 ( 2 ) + Θ 12 ( 1 ) a 2 ( 2 ) + Θ 13 ( 1 ) a 3 ( 2 ) ) h_{\Theta }(x)=a_{1}^{(3)}=g(\Theta _{10}^{(1)}a_{0}^{(2)}+\Theta _{11}^{(1)}a_{1}^{(2)}+\Theta _{12}^{(1)}a_{2}^{(2)}+\Theta _{13}^{(1)}a_{3}^{(2)}) hΘ(x)=a1(3)=g(Θ10(1)a0(2)+Θ11(1)a1(2)+Θ12(1)a2(2)+Θ13(1)a3(2))
2、向量化计算
将上述计算公式向量化以后如下所示:
x = [ x 0 x 1 x 2 x 3 ] z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) ] x=\begin{bmatrix} x_{0}\\ x_{1}\\ x_{2}\\ x_{3} \end{bmatrix}\quad\quad z^{(2)}=\begin{bmatrix} z_{1}^{(2)}\\ z_{2}^{(2)}\\ z_{3}^{(2)} \end{bmatrix} x=⎣⎢⎢⎡x0x1x2x3⎦⎥⎥⎤z(2)=⎣⎢⎡z1(2)z2(2)z3(2)⎦⎥⎤
a ( 1 ) = x z ( 2 ) = Θ ( 1 ) a ( 1 ) a ( 2 ) = g ( z ( 2 ) ) a^{(1)}=x\quad\quad z^{(2)}=\Theta ^{(1)}a^{(1)}\quad\quad a^{(2)}=g(z^{(2)}) a(1)=xz(2)=Θ(1)a(1)a(2)=g(z(2))
a 0 ( 2 ) = 1 z ( 3 ) = Θ ( 2 ) a ( 2 ) h Θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) a^{(2)}_0=1\quad\quad z^{(3)}=\Theta ^{(2)}a^{(2)}\quad\quad h_{\Theta }(x)=a^{(3)}=g(z^{(3)}) a0(2)=1z(3)=Θ(2)a(2)hΘ(x)=a(3)=g(z(3))
这个计算 h ( x ) h(x) h(x) 的过程,也成为前向传播,因为我们从输入单元的激活项开始,然后进行前向传播给隐藏层计算隐藏层的激活项,然后我们继续前向传播,并计算输出层的激活项。
如果把前向传播前面的部分盖住如下图所示:
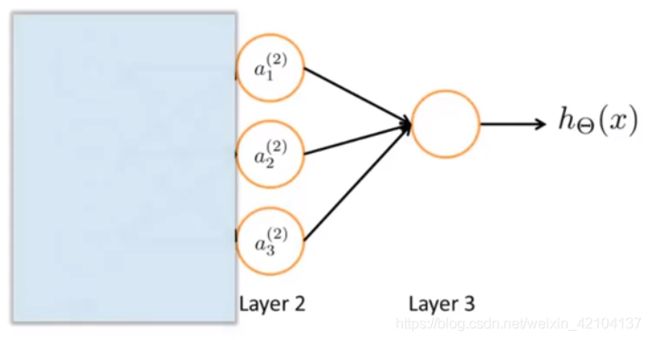
剩下的部分,实际上是实现的logistic回归。
特征项 a 1 a_1 a1, a 2 a_2 a2, a 3 a_3 a3 是学习得到的函数输入值,具体来说,就是从第一层映射到第二层的函数,这个函数由其他参数 Θ ( 1 ) \Theta^{(1)} Θ(1) 决定。
所以在神经网络中,它没有用输入特征值 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3 来训练Logistic回归,而是自己训练Logistic回归的输入值 a 1 a_1 a1, a 2 a_2 a2, a 3 a_3 a3 ,根据 Θ ( 1 ) \Theta^{(1)} Θ(1) 的不同,有时会训练出很有趣和复杂的特征,这样可以得到一个更好的假设函数,比使用原始的 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3 输入值得到的假设更好。
当然我们也可以用别的图来表示神经网路,如下图所示:

神经网路中神经元的连接方式称为神经网络的架构,架构是指不同神经元的连接方式。
3、例子与理解
神经网络来拟合逻辑关系AND
例: x 1 , x 2 ∈ 0 , 1 x_{1},x_{2}\in {0,1} x1,x2∈0,1 y = x 1 A N D x 2 y=x_{1}\quad AND \quad x_{2} y=x1ANDx2拟合过程:
神经元如下所示:

S型激活函数如下图所示:

神经网络的计算如下所示: h Θ ( x ) = g ( − 30 + 20 x 1 + 20 x 2 ) h_{\Theta }(x)=g(-30+20x_1+20x_2) hΘ(x)=g(−30+20x1+20x2)
计算结果如下所示:

从圈出的一列中可以看出拟合很成功,与AND的结果一致,当赋值为-10,20,20时,可以实现OR。
另外计算 N O T NOT NOT X 1 X_1 X1如下图所示:

根据以上所述,我们得到以下结论:
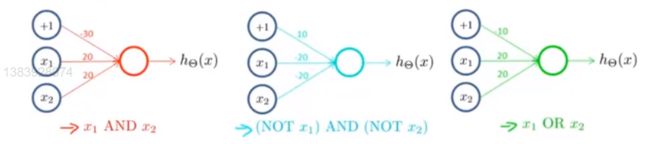
再举个复杂点的栗子:拟合 x 1 x_1 x1 X N O R XNOR XNOR x 2 x_2 x2
我们将以上的结论组合起来形成新的神经网路如下所示:

4、神经网络解决多元分类
要想用神经网络解决多元分类问腿,采用的方法本质上是一对多法的拓展,举个栗子:假设我们要将输入的图片分为以下四类:
我们要做的就是建立一个有四个输出神经元的神经网络,这个神经网络的输出是一个含4个数的向量,并分别用这四个神经元来判断类别:

当 h ( Θ ) ≈ [ 1 0 0 0 ] h(\Theta )\approx \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} h(Θ)≈⎣⎢⎢⎡1000⎦⎥⎥⎤ 时,代表行人, h ( Θ ) ≈ [ 0 1 0 0 ] h(\Theta )\approx \begin{bmatrix} 0\\ 1\\ 0\\ 0 \end{bmatrix} h(Θ)≈⎣⎢⎢⎡0100⎦⎥⎥⎤ 时,代表汽车,以此类推。
本章内容着重对于神经网络的入门和理解,后面一章我们会介绍神经网络的代价函数和算法等。