路径规划算法
目录
-
- 碰撞检测算法:
-
- 非cost_map:
-
- 针对二维平面中的多边形障碍物;
- cost_map:
-
- 检测直线是否与障碍物(cost>0)的节点碰撞
- 轨迹优化
-
- 梯度下降法
-
- 梯度的定义:
- 梯度下降法流程:
- 离散路点使用梯度下降
碰撞检测算法:
非cost_map:
针对二维平面中的多边形障碍物;
参考:https://blog.csdn.net/Azahaxia/article/details/115644042
线段与矩形:
python:
import numpy as np
class Rectangle:
def __init__(self, n):
#ox,oy 矩形左下角顶点 w 、h 宽和高
self.ox = n[0]
self.oy = n[1]
self.w = n[2]
self.h = n[3]
class Tool:
def __init__(self,delta):
#delta用于障碍物膨胀
self.delta = delta
def is_collide_with_rec(self,start, end, obs_rectangle):
obs_vertex = self.get_obs_vertex(obs_rectangle)
#v1, v2, v3, v4 矩形四个顶点
for (v1, v2, v3, v4) in obs_vertex:
#print(v1, v2, v3, v4)
if self.is_intersect_rec(start, end, v1, v2):
return True
if self.is_intersect_rec(start, end, v2, v3):
return True
if self.is_intersect_rec(start, end, v3, v4):
return True
if self.is_intersect_rec(start, end, v4, v1):
return True
return False
def get_obs_vertex(self,obs_rectangle):
delta = self.delta
obs_list = []
vertex_list = [[obs_rectangle.ox - delta, obs_rectangle.oy - delta],
[obs_rectangle.ox + obs_rectangle.w + delta, obs_rectangle.oy - delta],
[obs_rectangle.ox + obs_rectangle.w + delta, obs_rectangle.oy + obs_rectangle.h + delta],
[obs_rectangle.ox - delta, obs_rectangle.oy + obs_rectangle.h + delta]]
obs_list.append(vertex_list)
#print(obs_list)
return obs_list
def is_intersect_rec(self, start, end, a, b):
l1 = [a[0]-start[0],a[1]-start[1]]
l2 = [b[0]-start[0],b[1]-start[1]]
l3 = [end[0]-start[0],end[1]-start[1]]
m1=np.cross(l3,l1); n1=np.cross(l3,l2)
#print(m1,n1)
if m1==0 and (a[0]-start[0])*(a[0]-end[0])<=0 and (a[1]-start[1])*(a[1]-end[1])<=0 :
return True
if n1==0 and (b[0]-start[0])*(b[0]-end[0])<=0 and (b[1]-start[1])*(b[1]-end[1])<=0 :
return True
l4= [start[0]-a[0],start[1]-a[1]]
l5= [end[0]-a[0],end[1]-a[1]]
l6= [b[0]-a[0],b[1]-a[1]]
m2=np.cross(l6,l4); n2=np.cross(l6,l5)
#print(m2,n2)
if m2==0 and (start[0]-a[0])*(start[0]-b[0])<=0 and (start[1]-a[1])*(start[1]-b[1])<=0:
return True
if n2==0 and (end[0]-a[0])*(end[0]-b[0])<=0 and (end[1]-a[1])*(end[1]-b[1])<=0:
return True
if (m1*n1)<0 and (m2*n2)<0:
return True
return False
if __name__ == '__main__':
rec=Rectangle([1,1,1,1])
tool=Tool(0)
start=[0,0];end=[1,1]
res = tool.is_collide_with_rec(start,end,rec)
print(res)
C++:
#include
#include cost_map:
检测直线是否与障碍物(cost>0)的节点碰撞
参考:https://blog.csdn.net/u014028063/article/details/80917486?spm=1001.2014.3001.5506
#include轨迹优化
梯度下降法
梯度的定义:
如一元函数: y = f ( x ) y=f(x) y=f(x)
梯度就是函数的导数,即
∇ f ( x ) = f ′ ( x ) \nabla f(x) = f'(x) ∇f(x)=f′(x)
若为多元函数,则梯度为函数的偏微分,即
∇ f ( x 1 , x 2 , . . x n ) = ∂ f x 1 i 1 + ∂ f x 2 i 2 + . . . + ∂ f x n i n \nabla f(x_1,x_2,.. x_n) =\frac{\partial f}{x_1} i_1 + \frac{\partial f}{x_2} i_2 +...+ \frac{\partial f}{x_n} i_n ∇f(x1,x2,..xn)=x1∂fi1+x2∂fi2+...+xn∂fin
梯度下降法流程:
- 设定参数 η (步长),ε (误差),设定自变量(x1,x2,… xn)的取值(a1,a2,…an);
- 求出各自变量(x1,x2,… xn)在取值(a1,a2,…an)时的偏导数,
f ′ ( x m ) = ∂ f ∂ x m a m f'(x_m) =\frac{\partial f}{\partial x_m}a_m f′(xm)=∂xm∂fam
利用偏导数求出下一次迭代的新的变量取值(a1’,a2’,…an’)
a m ′ = a m − η f ′ ( x m ) = a m − η ∂ f ∂ x m a m a_m' = a_m -\eta f'(x_m) = a_m -\eta \frac{\partial f}{\partial x_m}a_m am′=am−ηf′(xm)=am−η∂xm∂fam - 判断
Δ a m = a m − a m ′ < ϵ \Delta am =a_m - a_m' < \epsilon Δam=am−am′<ϵ
若成立,则退出迭代,求解出(a1’,a2’,…an’)为目标自变量取值;
若不成立,则令(a1,a2,…an)=(a1’,a2’,…an’),并回到第2步,继续迭代。
离散路点使用梯度下降
示例:
如下图为一条离散路径,共7个路点,优化目标为在路径不碰到障碍物的情况下最优化路径。

为简单起见,这里的优化目标设置为路径的长度代价。
设路径表达式为
l ( p 1 , p 2 , . . . p n ) l(p_1,p_2,...p_n) l(p1,p2,...pn),其中p1,p2,…pn为图上的路点,有pm=(xm,ym)
路径代价函数
c o s t = f ( l ( p 1 , p 2 , . . . p n ) ) cost =f(l(p_1,p_2,...p_n)) cost=f(l(p1,p2,...pn))
f函数是对路径求长度的函数,那么优化目标就是让路径长度最短。
对于离散路径不是一个连续函数,是无法求梯度/导数,那就使用伪梯度。
对p2点求梯度方向,即为p2 垂直于p1 p3的连线的方向,如下图所示。
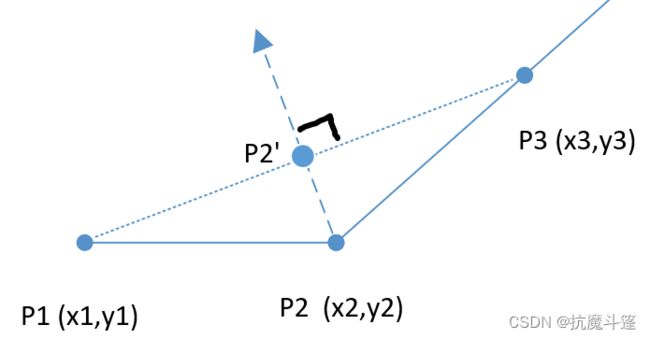
从直观上讲,将p2坐标改为两垂线的焦点p2’会使得路径更短,因为有
p1p2 + p2p3 > p1p2’ + p2’p3。那么将p2点向p2’点方向移动一小个步长,也会使得路径长度更短。
那么对出了首尾两端的路径点都进行这样的操作,则新的路径点如下图:

p2、p4、p5都进行了梯度下降,如红点所示,p3、p6则因为已经在最优位置了,不需要操作,新的路径如红线所示。在使用伪梯度下降时,需要确保路径不会于障碍物发生碰撞。
并对新的路径点求new cost,判断
c o s t = f ( l ( p 1 , p 2 , . . . p n ) ) − c o s t = f ( l ( p 1 ′ , p 2 ′ , . . . p n ′ ) ) < ε cost =f(l(p_1,p_2,...p_n)) - cost =f(l(p_1',p_2',...p_n')) < ε cost=f(l(p1,p2,...pn))−cost=f(l(p1′,p2′,...pn′))<ε
是否成立,成立则结束迭代,找到局部最优路径;否则将继续新一轮梯度下降迭代。