线性回归建模及模型诊断

目录

一、建模背景及目的及数据源说明

二、描述性分析

        2.1 连续自变量与连续因变量的相关性分析

        2.2 二分类变量与连续变量的相关性分析

        2.3 多分类变量与连续变量的相关性分析

三、模型建立与诊断

3.1 一元线形回归及模型解读

 3.2 残差可视化分析

3.3 多元线性回归

---

一、建模背景及目的及数据源说明

        本案例数据来源于常国珍等人的《Python数据科学》一书第7章中的信用卡公司客户申请信息（年龄、收入、地区等信息）以及已有开卡客户的申请信息和信用卡消费信息数据，案例希望通过对该数据的分析和建模，根据已有的开卡用户的用户信息和消费来线形回归模型，来预测未开卡用户的消费潜力。数据下载见如下链https://download.csdn.net/download/baidu_26137595/85101874

数据读入及示例：

raw = pd.read_csv('./data/creditcard_exp.csv', skipinitialspace = True)
raw.head()

数据字段及说明：

Acc： 是否开卡， 为0说明未开卡，对应的 avg_exp 为NaN；为1说明已开卡，对应avg_exp有值

avg_exp： 月均信用卡支出

avg_exp_ln：月均信用卡支出的对熟

gender : 性别

Ownrent： 是否自有住房

Selfempl： 是否自谋职业

Income：收入

dist_home_val： 所住小区均价 w

dist_avg_income： 当地人均收入

age2： 年龄的平方

high_avg： 高出当地平均收入

edu_class：教育等级，0、1、2、3 依次是小学、初中、高中、大学

二、描述性分析

首先可筛选Acc为1的数据，分别以avg_exp为因变量，其余变量为自变量进行数据探索，主要是发现自变量和因变量是否有线形关系。

raw_1 = raw[raw['Acc'] == 1]

2.1 连续自变量与连续因变量的相关性分析

首先对连续变量和目标变量进行相关性分析，因变量avg_exp为连续变量，一般可以用相关系数来看其线形相关性。

cons_vasr = ['avg_exp', 'avg_exp_ln', 'Age', 'Income', 'dist_home_val', 'dist_avg_income', 'age2', 'high_avg']
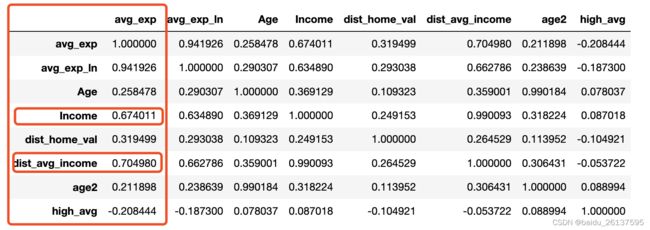
raw_1[cons_vasr].corr()vg']].corr()

结果如下，可以看到收入 Income 和当地人均收入 dist_avg_income这两个变量和avg_exp月均信用卡支出有较强的相关性，同时观察自变量间的相关性可发现人均收入 Income 和当地人均收入  dist_avg_income 之间也有较强的相关性，相关系数为0.99，说明接下来我们可以把这两个变量加入模型，但要注意可能会存在多重共线性。

2.2 二分类变量与连续变量的相关性分析

分类变量和连续变量之间的相关性可以用t检验进行，接下来以是否自有住房 Ownrent 变量 和 月均收入之间进行相关性检验。首先查看Ownrent 不同取值的数量以及avg_exp均值分布情况如何：

pd.pivot_table(raw_1, values = ['avg_exp'], index = ['Ownrent']
    , aggfunc = {'avg_exp': ['count', np.mean]})

 接着分别对 Ownrent 为0、1的 avg_exp 进行t检验：

import scipy.stats as st   # 引入scipy.stats进行t检验
# 创建变量
Ownrent_0 = raw_1[raw_1['Ownrent'] == 0]['avg_exp'].values
Ownrent_1 = raw_1[raw_1['Ownrent'] == 1]['avg_exp'].values

st.ttest_ind(Ownrent_0, Ownrent_1, equal_var = True)

 p值为0.01 < 0.05，可以拒绝原假设，即认为是否自有住房和月均信用卡支出是相关的。

2.3 多分类变量与连续变量的相关性分析

多分类变量和连续变量之间的相关性检验可以用多次t检验进行，但较为繁琐，用方差分析进行快速检验相关性，然后再运用多重检验查看具体是哪些处理之间存在差异。以教育水平edu_class为例进行分析，同理首先查看分布

raw_1.pivot_table(index = 'edu_class', values = ['avg_exp']
    , aggfunc={'avg_exp': ['count', np.mean]})

可以看到不同教育水平之间消费水平有明显差异，接下来通过方差分析进行检验差异是否明显。

from statsmodels.stats.anova import anova_lm #引入anova_lm进行方差分析
from ststsmodels.stats.formula import ols    #引入ols进行线性回归建模

lm = ols('avg_exp~C(edu_class)', data = raw_1).fit()  #C(edu_class) 将数值型的变量指定为分类型
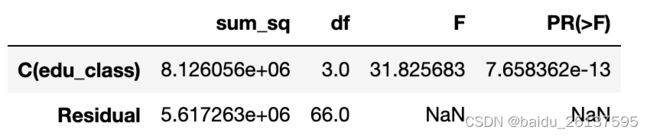
anova_lm(lm, typ = 2)

 

可以看到不同教育水平之间的月均消费支出之间的差异是显著的，继续用多重检验来看哪些处理之间是显著的。

from statsmodels.stats.multicomp import MultiComparison  # 引入MultiComparison进行tukey多重检验
mc = MultiComparison(raw_1['avg_exp'],raw_1['edu_class'])
tukey_result = mc.tukeyhsd(alpha = 0.5)
print(tukey_result)

结果是每个处理之间因变量差异的显著性，最后一列reject都为True说明各组之间均存在显著差异。

三、模型建立与诊断

3.1 一元线性回归及模型解读

以Income为自变量，以avg_exp为因变量建立一元线形回归并对模型结果进行解释

lm_1 = ols('avg_exp ~ Income', data = raw_1).fit()
print(lm_1.summary())

首先从第一部分可以看到R^2为0.454，整个模型的F检验p值小于0.05，说明模型通过显著性检验。

其次模型结果的第二块也表明自变量和截距也通过显著性检验。

 最后一部分主要是对残差进行检验，左侧Omnibus、Prob(Omnibus)主要是对偏度Skew和峰度Kurtosis进行检验，正态分布的偏度为0，峰度为3，模型的Prob(Omnibus)值为0.156大于0.05，说明不能拒绝残差符合正态分布。

右侧Durbin-Watson主要是对残差的自相关性进行检（改检验可表示为，为残差之间的相关系数），Durbin-Watson的取值范围是0-4，越接近2说明残差不存在自相关性，越接近0说明存在正相关，越接近4说明存在负相关性。

右侧Jarque-Bera (JB)、Prob(JB)是对残差正态性检验，可以用来判断残差是否符合正态分布，本案例中Prob(JB)值为0.173 > 0.05，基不能拒绝残差服从正态分布。

右侧Cond. No.是多重共线性检验，该值越大，共线性越严重。

整体上看模型虽然拟合效果没那么好，但是显著性通过了检验。接下来看一下模型具体的系数，Income的系数为97.7说明模型收入越高信用卡消费越高，是符合业务预期的。

 3.2 残差可视化分析

接下来对残差进一步进行可视化分析，主要看残差是否满足以下几个假定，并尝试通过对自变量、因变量进行调整来优化模型。首先来回顾一下残差需要满足的几个假定：

a.残差的要服从均值为0，方差为的正态分布；

b.残差之间要相互独立

c.残差和自变量没有相关性

（1）通过残差图进行模型优化

模型avg_exp ~ Income的自变量与残差分布图、残差qq图、模型拟合情况图即自变量与因变量及其预测值的图像

lm_1 = ols('avg_exp ~ Income', data = raw_1).fit()   # 建模
raw_1['resid_1'] = lm_1.resid  # 模型残差
raw_1['resid_1_rank'] = raw_1['resid_1'].rank(ascending = False, pct =  True)   # 计算残差的百分位数
raw_1['pred_1'] = lm_1.predict()   # 添加预测值


plt.figure(figsize = (20, 6))

# 自变量与残差分布图
ax1 = plt.subplot(131)
ax1.scatter('Income', 'resid', data = raw_1)
ax1.set_title('Income & resid')

# 残差的qq图
ax2 = plt.subplot(132)
stats.probplot(raw_1['resid_1_rank'], dist = 'norm', plot = ax2)

# 模型拟合情况图，自变量与因变量以及模型预测值
ax3 = plt.subplot(133)
ax3.scatter('Income', 'avg_exp', data = raw_1)
ax3.plot('Income', 'pred_1', data = raw_1, color = 'red')
ax3.legend()
ax3.text(12, 1920, 'pred func R^2: %.2f'% lm_1.rsquared)
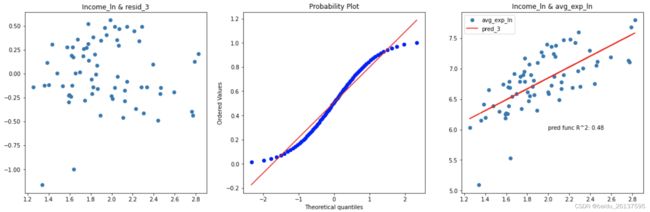
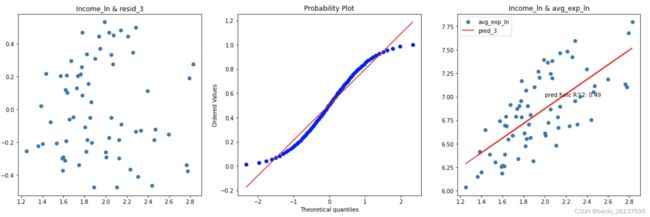
ax3.set_title('Income & avg_exp')

 从第一个自变量和残差散点图可以看出，残差基本符合对称分布，但随着自变量增大，残差也在变大，存在方差不齐的情况。第二个图残差的qq图可以看出，残差近似正态分布。第三个图可以看模型的拟合效果并不是很好，R^2只有0.45。对avg_exp取对数，能够改善预测值越大残差越大的情况，但由于只对因变量取对数导致模型不好解释，对自变量Income同时取对数，代码和以上类似，只是改变因变量和自变量形式而已，以下是残差图，可以看到残差的异方差现象被有效的抑制，并且R^2也得到了提高。

（2）通过残差图发现强影响点

仔细观察以上图像结果，左下侧有两个较为异常的数据，对模型的拟和效果有较大的影响， 对于这种影响较大的可将其进行删除并重新建模：

# 计算学生化残差
raw_1['resid_t'] = (raw_1['resid_2'] - raw_1['resid_2'].mean())/raw_1['resid_2'].std() 
raw_1[abs(raw_1['resid_t']) > 2]  # 将残差大于2的筛选出来

将强影响点删除后，得到的结果如下，模型结果更稳定。 

3.3 多元线性回归

上一篇文章有说到多重共线性会对模型产生致命的影响，用方差膨胀因子来处理的话会非常繁琐。通过正则化处理如Lasso回归，能够产生某些严格等于0的系数，从而达到变量筛选的目的。接下来以Lasso为例，首先用LassoCV来找到最优的alpha。由于statsmodels中的ols的fit_regularized方法没有很好的实现，所以用sklearn中linear_model模块来进行建模

from sklearn.preprocessing import StandardScaler  # sklearn进行线性回归前必须要进行标准化
from sklearn.linear_model import LassoCV   # Lasso的交叉验证方法

con_xcols = ['Age', 'Income', 'dist_home_val', 'dist_avg_income']
scaler = StandardScaler()
X = scaler.fit_transform(raw_1[con_xcols])
y = raw_1['avg_exp_ln']

lasso_alphas = np.logspace(-3, 0, 100, base = 10)
lcv = LassoCV(alphas = lasso_alphas, cv = 10)
lcv.fit(X, y)

print('best alpha %.4f' % lcv.alpha_)
print('the r-square %.4f' % lcv.score(X, y))

 接下来画出不同alpha下的岭迹图，来看alpha值对系数的影响

from sklearn.linear_model import Lasso
coefs = []
lasso = Lasso()
for i in lasso_alphas:
    lasso.set_params(alpha = i)
    lasso.fit(X, y)
    coefs.append(lasso.coef_)

ax = plt.gca()
ax.plot(lasso_alphas, coefs)
ax.set_xscale('log')
ax.set_xlabel('$\\alpha$')
ax.set_ylabel('coefs value')

 从图中可以看到随着alpha的增大，系数不断在减小，有些系数会优先收缩为0，再继续增大时所欲系数都会为0，通过该特性从而达到变量筛选的目的。将LassoCV得到的系数打印出来，可以看到用户月均信用卡支出和当地小区均价、当地人均收入成正比，当地人均收入水平的影响更大。

 以上就是线形回归在应用时的注意事项。