ST-GCN的学习之路（二）源码解读 （Pytorch版）
ST-GCN的学习之路（二）源码解读 （Pytorch版）
- 引言
- 代码分析
-
- 核心代码分析 net网络
-
- graph.py
-
- self.get_edge
- self.get_hop_distance
- self. get_adjacency
- st-gcn.py
-
- 网络的输入
- 网络的结构
-
- GCN模块
- TCN模块
- 其他代码
- 总结
-
- 博客参考
引言
上一篇我们阅读了st-gcn的论文，了解了st-gcn的整体思想。这一篇博客我准备就官方推出的Pytorch源码进行详细的分析（会具体到每一句，每一个原理），如果有不足和错误之处希望各位多多指出，欢迎交流，共同进步。（由于博主目前还是一名大三学生，由于学业的事也不能经常更新博客和回应提问，请各位海涵）
论文原文：Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition
ST-GCN（Pytorch）官方源码：https://github.com/yongqyu/st-gcn-pytorch
代码分析
核心代码分析 net网络
核心代码共分3个文件，在net文件夹下，分别为graph.py, tgcn.py, st-gcn.py。其中graph.py中包含邻接矩阵的建立和结点分组策略（下面会详细介绍结点分组策略的含义）、st-gcn.py包含整个网络部分的结构和前向传播方法、tgcn.py主要是空间域卷积的结构和前向传播方法。
graph.py
首先我们先来看下graph.py,类Graph的构造函数使用了self.get_edge、self.hop_dis、self.get_adjacency，在这个模块主要分了3类：
- 邻接矩阵的建立
- 归一化以及快速图卷积的与处理
- 权值的分组
class Graph():
def __init__(self,
layout='openpose',
strategy='uniform',
max_hop=1,
dilation=1):
self.max_hop = max_hop
self.dilation = dilation
self.get_edge(layout) # 确定图中结点间边的关系
self.hop_dis = get_hop_distance(self.num_node, self.edge, max_hop=max_hop)# 获得邻接矩阵
self.get_adjacency(strategy)
...
self.get_edge
这里采用的是OpenPose的节点进行举例，需要指出的是作者的节点连接顺序与本来OP中提供的输出格式的连接顺序是不同的，具体的体现在(2,8)(5,11)点的连接，这样的连接对结果没有影响，但是也不能简单地认为将OP中的节点pair改为st-gcn中的顺序就匹配了，因为不能忘记OP中的PAF的训练是按照(1,8)(1,11)进行训练的。
def get_edge(self, layout):
if layout == 'openpose':
self.num_node = 18
self_link = [(i, i) for i in range(self.num_node)]
neighbor_link = [(4, 3), (3, 2), (7, 6), (6, 5), (13, 12), (12,
11),
(10, 9), (9, 8), (11, 5), (8, 2), (5, 1), (2, 1),
(0, 1), (15, 0), (14, 0), (17, 15), (16, 14)]
self.edge = self_link + neighbor_link
self.center = 1
elif layout == 'ntu-rgb+d':
self.num_node = 25
...!
从源码可以看出来center点是neck(1)点。注意如果两点都邻接不可到中心点即距离都是inf，那么算作远心点。
self.get_hop_distance
def get_hop_distance(num_node, edge, max_hop=1):
A = np.zeros((num_node, num_node))
for i, j in edge: #构建邻接矩阵
A[j, i] = 1
A[i, j] = 1
# compute hop steps
hop_dis = np.zeros((num_node, num_node)) + np.inf
transfer_mat = [np.linalg.matrix_power(A, d) for d in range(max_hop + 1)]
arrive_mat = (np.stack(transfer_mat) > 0) # transfer_mat是list类型，需要将list堆叠成一个数组才能进行>操作
for d in range(max_hop, -1, -1):
hop_dis[arrive_mat[d]] = d
return hop_dis
这一段代码中获得了带自环的邻接矩阵（是18乘18的方阵），非连接处是inf
self. get_adjacency
def get_adjacency(self, strategy):
valid_hop = range(0, self.max_hop + 1, self.dilation) # 合法的距离值：0或1
adjacency = np.zeros((self.num_node, self.num_node))
for hop in valid_hop:
adjacency[self.hop_dis == hop] = 1 # 将0|1的位置置1,inf抛弃
normalize_adjacency = normalize_digraph(adjacency)#图卷积的预处理
...
elif strategy == 'spatial': # 如果按论文的第三种划分方式
A = []
for hop in valid_hop:
a_root = np.zeros((self.num_node, self.num_node))
a_close = np.zeros((self.num_node, self.num_node))
a_further = np.zeros((self.num_node, self.num_node))
for i in range(self.num_node):
for j in range(self.num_node):
if self.hop_dis[j, i] == hop: # 如果结点j和结点i是邻结点
# 比较结点i和结点j分别到中心点的距离，中心点默认为为openpose输出的1结点
if self.hop_dis[j, self.center] == self.hop_dis[ i, self.center]:
a_root[j, i] = normalize_adjacency[j, i]
elif self.hop_dis[j, self. center] > self.hop_dis[i, self.center]:
a_close[j, i] = normalize_adjacency[j, i]
else:
a_further[j, i] = normalize_adjacency[j, i]
if hop == 0:
A.append(a_root) # A的第一维第1个矩阵:self distance matrix 对角阵
else:
A.append(a_root + a_close) # A的第一维第2个矩阵:列对结点到中心点的距离比行对应点到中心点的距离近或者相等（都为inf)
A.append(a_further) # A的第一维第3个矩阵:列对应结点到中心点的距离比行对应点到中心点的距离远
A = np.stack(A)
self.A = A
# 输出A的shape（3，18，18）
...
# 图卷积的预处理
def normalize_digraph(A):
Dl = np.sum(A, 0) #计算邻接矩阵的度
num_node = A.shape[0]
Dn = np.zeros((num_node, num_node))
for i in range(num_node):
if Dl[i] > 0:
Dn[i, i] = Dl[i]**(-1) #由每个点的度组成的对角矩阵
AD = np.dot(A, Dn)
return AD
这段代码将会输出一个（3，18，18）的权值分组A矩阵。那么这个矩阵是怎么来的呢?这就要追溯到论文里提到的三种划分方法了：
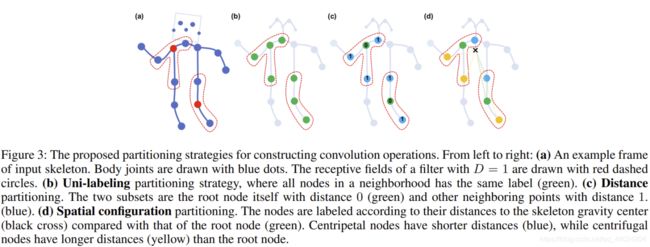
- Uni-labeling，全部 B ( v t i ) B(v_{ti}) B(vti)分为一个subset，但是这样会失去局部的特点属性。只需要将K = 1，且 l t i ( v t j ) = 0 l_{ti}(v_{tj}) = 0 lti(vtj)=0即可，这就表明了只有1个类，且所有 v t i v_{ti} vti的subset序号为0。
- Distance partitioning 按照距离来分子集，分为root点和其他点。只需要将K = 2，且 l t i ( v t j ) = d ( v t j , v t i ) l_{ti}(v_{tj}) = d(v_{tj},v_{ti}) lti(vtj)=d(vtj,vti)即可，因为D=1,所以d()只能为0-1之间的两个值。
- Spatial configuration partitioning 根据空间的分区，论文中分为K = 3 个子集，分类依据是近心点、远心点、自身点，代码中实现时采用openpose 1点作为中心点。
（附：这里的 l t i ( v t j ) l_{ti}(v_{tj}) lti(vtj)是论文中提到的映射函数，它的作用是把第 i i i个节点周围的 j j j个结点的集合划分为 K K K个子集。）
代码中采用spatial划分方法，根据列对应的结点跟行对应的结点分别到中心点的距离（相等，列小于行，列大于行）将normalize_adjacency归一化后的矩阵的划分成三个权值矩阵，这三个权值矩阵的shape=(18,18),经过stack方法后堆叠成(3,18,18)
D矩阵，在paper中是没有提到D矩阵的，只是提出了一种图卷积的公式，在这里只需要知道D是有i节点的度所组成的对角矩阵。使用的图卷积公式是 D − 1 A X D^{-1}AX D−1AX
st-gcn.py
网络的输入
整个网络的输入是一个(N = batch_size,C = 3,T = 300,V = 18,M = 2)的tensor。
N 视频个数
C = 3 (X,Y,S)代表一个点的信息(位置+预测的可能性)
T = 300一个视频的帧数paper规定是300帧，不足的重头循环，多的clip
V 18 根据不同的skeleton获得的节点数而定，coco是18个节点
M = 2 人数，paper中将人数限定在最大2个人
def forward(self, x): # 整个Moule的forward函数
# data normalization
N, C, T, V, M = x.size() # 网络的输入(N = batch_size,C = 3,T = frame_num,V = 18(node_num),M = 2)
x = x.permute(0, 4, 3, 1, 2).contiguous()
x = x.view(N * M, V * C, T)
x = self.data_bn(x) # 输入层的batchNorm（V*C）
x = x.view(N, M, V, C, T)
x = x.permute(0, 1, 3, 4, 2).contiguous()
x = x.view(N * M, C, T, V) # 注意，这里网络输入将 N, C, T, V, M整合成了N，C，V，T。将batch和person_num维度整合了一起
# forwad st-gcn 这个地方有点坑，其实这个for gcn，importance应该改为for st-gcn， importance
for gcn, importance in zip(self.st_gcn_networks, self.edge_importance):
x, _ = gcn(x, self.A * importance)
# global pooling
x = F.avg_pool2d(x, x.size()[2:])
x = x.view(N, M, -1, 1, 1).mean(dim=1)
# prediction
x = self.fcn(x)
x = x.view(x.size(0), -1)
return x
网络的结构
self.data_bn = nn.BatchNorm1d(in_channels * A.size(1))
self.st_gcn_networks = nn.ModuleList((
st_gcn(in_channels, 64, kernel_size, 1, residual=False, **kwargs0),
st_gcn(64, 64, kernel_size, 1, **kwargs),
st_gcn(64, 64, kernel_size, 1, **kwargs),
st_gcn(64, 64, kernel_size, 1, **kwargs),
st_gcn(64, 128, kernel_size, 2, **kwargs),
st_gcn(128, 128, kernel_size, 1, **kwargs),
st_gcn(128, 128, kernel_size, 1, **kwargs),
st_gcn(128, 256, kernel_size, 2, **kwargs),
st_gcn(256, 256, kernel_size, 1, **kwargs),
st_gcn(256, 256, kernel_size, 1, **kwargs),
))
# initialize parameters for edge importance weighting
if edge_importance_weighting:
self.edge_importance = nn.ParameterList([
nn.Parameter(torch.ones(self.A.size()))
for i in self.st_gcn_networks
])
else:
self.edge_importance = [1] * len(self.st_gcn_networks)
# fcn for prediction
self.fcn = nn.Conv2d(256, num_class, kernel_size=1)
可以看出模型是：
- 一个输入层的batchNorm(接受的通道数是in_channels#3 * A.size(1)#18 模型的输入是一个(N,C,T,V,M)的tensor
- 第二部分由10层st_gcn层构成
- 最后加一层全连接层
作者将第一层的st_gcn(in_channels, 64, kernel_size, 1, residual=False, kwargs0)不算作stgcn模块中，所以一共有9层。每一个st-gcn层都用residual模块来改进。可以在源码中看出来当通道数要增加时，作者使用1x1conv来进行通道的翻倍，另外使用stride = 2来完成pool的效果使得长宽减半。
从上面这张图上我们可以看出，一个ST-GCN层包含了一个GCN模块和一个TCN模块，另外，还有邻接矩阵和边权重矩阵（edge_importance）的内积，所要更新的模型参数也分为了两个方面：一是gcn和tcn内卷积核参数，二是edge_importance内的参数。下面来具体讲讲GCN模块和TCN模块，这也是我认为代码中的最难懂的部分。
GCN模块
gcn模块位于tgcn.py：
class ConvTemporalGraphical(nn.Module):
def __init__(self,
in_channels,
out_channels,
kernel_size,
t_kernel_size=1,
t_stride=1,
t_padding=0,
t_dilation=1,
bias=True):
super().__init__()
self.kernel_size = kernel_size # # 注意：这个keneral_size指的是空间上的kernal size，等于3，也等于划分策略划分的子集数K
self.conv = nn.Conv2d(
in_channels,
out_channels * kernel_size,
kernel_size=(t_kernel_size, 1), # Conv(1，1)
padding=(t_padding, 0),
stride=(t_stride, 1),
dilation=(t_dilation, 1),
bias=bias)
# tgcn.py
# forwad
# for gcn, importance in zip(self.st_gcn_networks, self.edge_importance):
# x, _ = gcn(x, self.A * importance)
# 注意在forward传入的A并不是单纯的self.A,而是self.A * importance
def forward(self, x, A):
assert A.size(0) == self.kernel_size
x = self.conv(x) # 这里输入x是(N,C,T,V),经过conv(x)之后变为（N，C*kneral_size,T,V）
n, kc, t, v = x.size()
x = x.view(n, self.kernel_size, kc//self.kernel_size, t, v)# 这里把keneral_size的维度单独拿出来，变成(N,K,C,T,V)
x = torch.einsum('nkctv,kvw->nctw', (x, A)) # 爱因斯坦约定求和法，下面会有介绍
return x.contiguous(), A
这段代码里最为重要的两句是：
x = self.conv(x)
x = torch.einsum(‘nkctv,kvw->nctw’, (x, A))
他们执行了一个这样的操作：
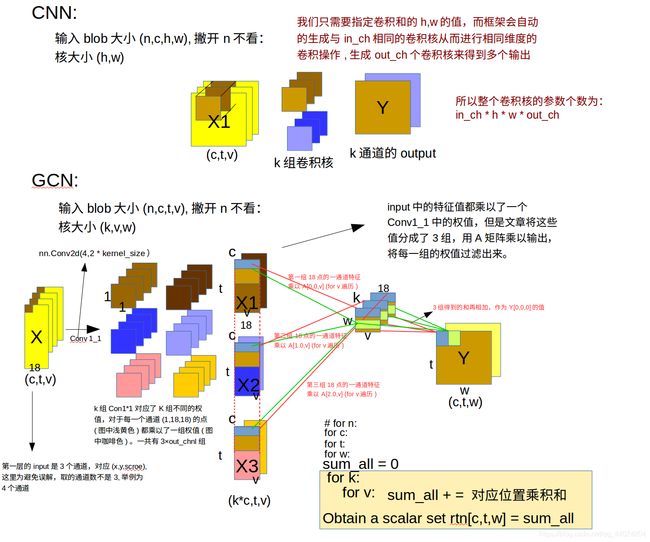这张图比较好的展示了上面两句代码的操作过程。首先，刚刚我们提到了输入是(N,C,T,V),假设我们令batch = 1，输入就变为了(C,T,V)。这样的输入非常像我们的一张图片（C，H，W）（RGB3通道，宽W，高H）。这时如果我们用CNN的角度来看的话T就对应了二维图上的纵轴，而V就对应了二维图上的横轴。RGB3通道对应了(x,y,置信度)也就是图结点的位置。好了，到这里我们需要返回到我们上面提到的三种划分权值子集的策略了，还记得我们把图上结点的位置划分为三个权重子集并把他们堆叠成了一个A矩阵（3，18，18）吗？现在我们要用到它了（用到它体现了我们对不同类型结点的划分权值子集的思想，同时也体现了人体关节之间结点的空间联系，因为我们的T，V构成的2d维度并不能体现出来人体关节结点在空间上的联系）
具体是怎么用到A的呢？这里的self.conv的卷积核大小是(1, 1)，是一个1x1的卷积层，以第一层举例，在第一层输入channel为4，要求输出channel为2，时就相当于把输入的(c=4, t=300, v=18)用了三组不同的卷积核（这里为深棕浅棕、深蓝浅蓝、粉黄三组），每组卷积下来可以得到C=2的三组特征图**（k*c,t,v）**。而这一层1x1卷积的目的就很明显了，就是要把把输入的通道C的特征升维K倍，在x = self.conv(x)之后将输出整合成了(N,K,C,V,T),也就是说把刚刚升的K倍作为单独的维度抽取出来了，这里有一个图能够更形象的理解这个卷积(1, 1)的过程。
这时x是(N,K,C,T,V),而A是(K,V,V),接下来使用einsum（爱因斯坦求和约定，不了解的可以百度）对A和x进行维度融合。einsum( )相当于是：
O u t n c t w = ∑ k ∑ v x n k c t v A k v w Out_{nctw}=\sum_{k}\sum_{v}x_{nkctv}A_{kvw} Outnctw=k∑v∑xnkctvAkvw这个公式可以理解为根据邻接矩阵中的邻接关系做了一次邻接节点间的特征融合，输出就变回了(N*M, C, T, V)的格式。具体的图形化理解可以参考上面的GCN那个图，就是得到的（k*c(也是output_channel),v,t）看成k组的 (c,v,t),每一组的对应通道上同一个t下v方向18个点与A中每一个对应通道下的v方向做点积（这个点积我个人认为可以看作是是一个图卷积，即18个点的2d位置和他们之间相对位置的一个融合，图每个i结点的周围j结点的特征朝着这个i结点流入。另外就是你A矩阵不是把人家周围j个结点分成3组了吗，也就是你A的3维度加起来才能表示出来一个结点周围完整的连接（也可以理解为只有你划分子集K=3的加起来才能还原出i结点周围的所有j结点的集合，只有你把这这A的三通道卷积结果加起来才能实现以i为中心j个周围结点的信息的流入））,因此把这3个通道相加得出output上的一个通道的结果。
到这里GCN模块就讲完了，接下来讲TCN模块。
TCN模块
在GCN后面紧跟着就是TCN的模块，该模块让网络在时域中进行特征的提取，类似与LSTM，GCN的输出是一个(n,c,t,w)的blob，在TCN中可以简单的理解为和CNN的输入格式一样。上面也说了，纵轴是时间，横轴代表了18个结点。那么要整合不同时间上的结点特征，对应的就是在纵轴上进行卷积了。
self.tcn = nn.Sequential(
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=True),
nn.Conv2d(
out_channels,
out_channels, # 不改变chanl值
(kernel_size[0], 1),
(stride, 1), # stride可以控制t域的缩小，可当做poolling操作
padding,
),
nn.BatchNorm2d(out_channels),
nn.Dropout(dropout, inplace=True),
)
tcn是用(temporal_kernel_size, 1)的卷积核对t维度进行卷积运算。这部分相对于gcn就很好理解了，就是正常的卷积操作，对于同一个节点在不同t下的特征的卷积。
gcn中是在单个时间t的图上生成新的特征和特征交流，tcn是在时间维度上特征交流。
其他代码
暂且搁置，基本就是一些加载文件和数据集的代码，日后再来填坑(逃
总结
这篇ST-GCN着实NB，也让我头疼了好久，今天得以细细分析下来，实属不易。接下来这个系列我准备再出一篇复现教程（其实我已经复现过这篇论文，只不过之前是caffe版本的，这次准备用pytorch版本再复现一遍）和它的衍生出来的几篇paper的reading，欢迎大家关注和交流。^o^
博客参考
ST-GCN中，空域图卷积的可视化过程
st-gcn （图卷积和时间卷积）
有没有大佬讲解一下st-gcn论文源代码?