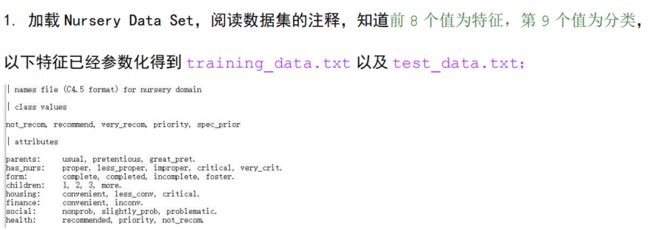
【ML实验4】多分类贝叶斯模型

实验代码获取 github repo
山东大学机器学习课程资源索引

---

实验目的

实验内容

数据集

构建多分类贝叶斯模型

这里的条件独立性指的是特征$x_j$之间相互独立，这是一个十分强的假设。

证明 Problem Set 2
思路主要是证明下面引理，用拉格朗日乘子法，对$p_y$求偏导变换一下可得。之后将目标似然函数分为两部分，一部分是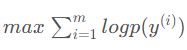，另一部分是，将标签或者特征出现频次视为权重，应用引理即可。
其实这个结论十分直观，发生多的自然越有可能发生，量化表达，将出现的频率作为对目标函数的贡献。

预测

拉普拉斯平滑

前面构建的模型是朴素贝叶斯，和贝叶斯估计的优化函数有点不同，后者结果在各个取值的频数增加一个$\lambda$，当$lambda=1$时称为拉普拉斯平滑，可以避免0/0的错误。

实验结果

混淆矩阵部分代码：

function confusion_matrix(actual,detected)
[mat,order] = confusionmat(actual,detected);
 
imagesc(mat);            %# Create a colored plot of the matrix values
colormap(flipud(gray));  %# Change the colormap to gray (so higher values are
                         %#   black and lower values are white)
                         
textStrings = num2str(mat(:),'%0.02f');  %# Create strings from the matrix values
textStrings = strtrim(cellstr(textStrings));  %# Remove any space padding
 
[x,y] = meshgrid(1:5);   %# Create x and y coordinates for the strings
hStrings = text(x(:),y(:),textStrings(:),...      %# Plot the strings
                'HorizontalAlignment','center');
midValue = mean(get(gca,'CLim'));  %# Get the middle value of the color range
textColors = repmat(mat(:) > midValue,1,3);  %# Choose white or black for the
                                             %#   text color of the strings so
                                             %#   they can be easily seen over
                                             %#   the background color
set(hStrings,{'Color'},num2cell(textColors,2));  %# Change the text colors
 
set(gca,'XTick',1:5,...                         %# Change the axes tick marks
        'XTickLabel',{'0','1','2','3','4'},...  %#   and tick labels
        'YTick',1:5,...
        'YTickLabel',{'0','1','2','3','4'},...
        'TickLength',[0 0]);
xlabel('Real Class');
ylabel('Predict Class');

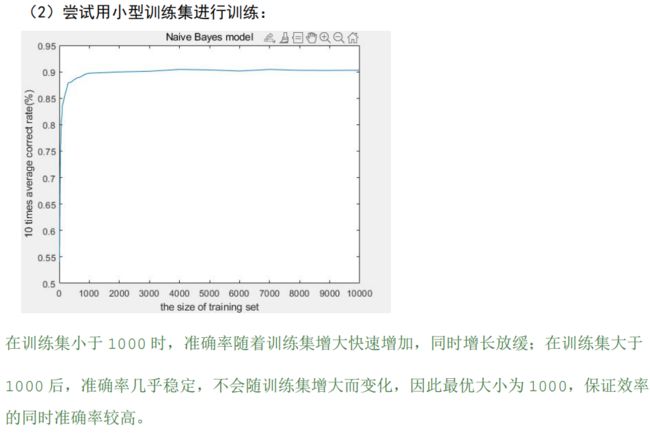
小数据集训练，对贝叶斯模型的效果影响甚微，而且效率上更优，主要是因为贝叶斯模型的训练是基于统计的，这和抛硬币去数正反是一个道理，符合大数定律，当一定硬币抛到一定次数，我们就可以确定正面出现50%，反面出现50%，当然随着标签和特征数增加，这个一定次数也会随之增加，和模型的复杂度相关。又问为什么训练会基于统计，解为什么会是特征或者标签的频率，因为贝叶斯最重要的假设，样本各个特征之间相互独立，没有关联，可以将视作一个个‘1’进行统计。

Conclusion