实验三 朴素贝叶斯分类

一、实验原理

        朴素贝叶斯分类器是分类算法集合中基于贝叶斯理论的一种算法。它不是单一存在的，而是一个算法家族，在这个算法家族中它们都有共同的规则。例如每个被分类的特征对与其他的特征对都是相互独立的。

假设

朴素贝叶斯基础假设是，对于每一个特征都有：

• 独立
• 相等

来支持输出结果。

可以这样理解这个概念：

• 我们假设没有特征对是相互依赖的。
• 其次，每个特征都有相同的权重（或者是重要性）。

注意：如果在现实情况中，这个假设就使得朴素贝叶斯不能一般性地正确了。实际上独立这个假设就根本不可能成立，但是又往往在实践中能够很方便地计算。

在进入朴素贝叶斯方程之前，要知道贝叶斯理论是十分重要的。

贝叶斯理论

贝叶斯理论指的是，根据一个已发生事件的概率，计算另一个事件的发生概率。贝叶斯理论从数学上的表示可以写成这样：

P(A|B)=P(B|A)P(A)P(B)

,在这里A和B都是事件， P(B)不为0。

• 基本上，只要我们给出了事件B为真，那么就能算出事件A发生的概率，事件B也被称为证据。
• P(A)是事件A的先验（先验概率，例如，在证据之前发生的概率）。证据是一个未知事件的一个属性值（在这里就是事件B）。
• P(A|B)是B的后验概率，例如在证据之后发生的概率。

我们可以这样用贝叶斯理论： 

P(y|X)=P(X|y)P(y)P(X)

在这里y是类变量，X是依赖特征向量（大小为n）： 

X=(x1,x2,x3,...,xn)

朴素假设

现在是时候为贝叶斯理论添加假设了，也就是每个特征之间都是相互独立的。所以我们可以将证据分成每个独立的部分。

如何两个事件A和B是相互独立的，那么有： 

P(AB)=P(A)P(B)

因此我们可以得到以下结果： 

P(y|x1,...,xn)=P(x1|y)P(x2|y)...P(xn|y)P(y)P(x1)P(x2)...P(xn)

于是又可以写成： 

P(y|x1,...,xn)=P(y)Πni=1P(xi|y)P(x1)P(x2)...P(xn)

因为分母与输入数据是常量相关的，所以我们可以除去这一项： 

P(y|x1,...,xn)∝P(y)Πni=1P(xi|y)

现在我们需要建立一个分类模型，我们用已知的类变量y的所有可能的值计算概率，并选择输出概率是最大的结果。数学表达式可以这么写： 

ŷ=argmaxyP(y)Πni=1P(xi|y)

所以最后剩下的只有P(y)与P(xi|y)的计算了。

请注意：P(y)也被称为类概率，P(xi|y)也被称为条件概率。

不同的朴素贝叶斯分类器差异主要在P(xi|y)分布的假设。

总结：

朴素贝叶斯分类常用于文本分类，尤其是对于英文等语言来说，分类效果很好。它常用于垃圾文本过滤、情感预测、推荐系统等。

第一阶段：准备阶段
在这个阶段我们需要确定特征属性，比如上面案例中的“身高”、“体重”、“鞋码”等，同时明确预测值是什么。并对每个特征属性进行适当划分，然后由人工对一部分数据进行分类，形成训练样本。

这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段：训练阶段

这个阶段就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率。

输入是特征属性和训练样本，输出是分类器。
第三阶段：应用阶段

这个阶段是使用分类器对新数据进行分类。

输入是分类器和新数据，输出是新数据的分类结果。
 

二、实验内容

设计一个贝叶斯分类器，对红酒进行分类。 

三、实验数据

        在http://archive.ics.uci.edu/ml/  网页上下载实验所用的 Wine 数据集。点击 Wine 数据集： 在页面上点击 Data Folder，下载 wine.data 数据。该实验的数据源是 W ine data,这是对位于意大利同一地区生产的三种不同类型的葡萄 酒做大量分析所得出的数据，  如图 1 所示。这些数据包括了三种酒中 13 种不同成分的具体 数量。13 种成分分别为: Alcohol, Malic acid, Ash, Alcalinity of ash , Magnesium, Total phenols , Flavanoids, Nonflavanoid phenols, Proanthocyanins, Color intensity, Hue, OD280/OD315 of diluted wines , Proline。在“wine.data"文件中，  每行代表一 种酒的样本，共有 178 个样本； 数据集共有 14 列，  其中，  第一列为类标志属性：  共三类，  分别记为“1”，“2”，  "3”；  后面的 13 列为每个样本的对应属性的样本值。第 1 类有59 个样本，  第 2 类有 71 个样本，  第 3 类 有 48 个样本。

四、代码 

#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;



//每一类中每一个成分的  平均值  标准差
struct node {

    double standardDeviation;

    double mean;

    node() {
        mean = 0;
        standardDeviation = 0;
    }

    explicit node(double ave, double standardDeviation) {
        mean = ave;
        this->standardDeviation = standardDeviation;
    }
};

class NaiveBayes {
private:

    vector> data;
    //储存原始数据的矩阵178*14

    vector> normalDistributionParameter;
    //3*13 储存每一类中成分的高斯分布概率的参数： 均值 方差

    vector prioriProbability;
    //1*3  储存每一类的先验概率


public:

    NaiveBayes();

    explicit NaiveBayes(string file);

    void readData(string &file, vector> &data);
    //从文件中读取数据到data

    void cmputePrioriProbability(vector> &data, vector &prioriProbability);
    //计算先验概率

    double computeMean(vector arr);
    //计算平均值

    double computeStandardDeviation(vector arr);
    //计算标准差

    void computeNormalDistributionParameter();
    //计算每一类中每组成分的 均值 方差

    double gaussianDistribution(double num, double ave, double standardDeviation);
    //计算高斯分布的概率密度

    void NaiveBayesClassifier(vector posteriorProbability);
    //根据计算的后验概率判断属于哪一类

    vector computePosteriorProbability(vector sample);
    //根据输入的数据，计算后验概率

};

//把string 转成基本数据类型
template
Type stringToNum(const string &str) {
    istringstream iss(str);
    Type num;
    iss >> num;
    return num;
}

void NaiveBayes::readData(string &file, vector> &data) {
    string num;
    ifstream fin;
    fin.open(file);
    if (!fin.is_open()) {
        cerr << "文件读取失败！请检查文件绝对路径是否正确！\n";

    }
    int counter = 0;
    int line = 0;
    do {
        if (counter == 13) {
            getline(fin, num, '\n');
            data[line][counter] = stringToNum(num);
            line++;
            if (line == data.size()) {
                break;
            }
            counter = 0;

        } else {
            getline(fin, num, ',');
            data[line][counter] = stringToNum(num);
            counter++;
        }
    } while (fin);
    fin.close();
}


NaiveBayes::NaiveBayes() {
    data.resize(178);
    for (int i = 0; i < data.size(); i++) {
        data[i].resize(14);
    }
    normalDistributionParameter.resize(3);
    for (int i = 0; i < normalDistributionParameter.size(); i++) {
        normalDistributionParameter[i].resize(13);
    }
    prioriProbability.resize(3);
}

NaiveBayes::NaiveBayes(string file) {
    data.resize(178);
    for (int i = 0; i < data.size(); i++) {
        data[i].resize(14);
    }
    normalDistributionParameter.resize(3);
    for (int i = 0; i < normalDistributionParameter.size(); i++) {
        normalDistributionParameter[i].resize(13);
    }
    prioriProbability.resize(3);
    readData(file, this->data);
    cmputePrioriProbability(this->data, this->prioriProbability);
    computeNormalDistributionParameter();
}

void NaiveBayes::cmputePrioriProbability(vector> &data, vector &prioriProbability) {
    for (int i = 0; i < prioriProbability.size(); i++) {

        double counter = 0;
        for (int j = 0; j < data.size(); j++) {
            if (data[j][0] == i + 1) {
                counter++;
            }
        }

        prioriProbability[i] = counter / data.size();
    }
}


double NaiveBayes::computeMean(vector arr) {

    double sum = 0;
    for (double i : arr) {
        sum += i;
    }
    return sum / arr.size();
}


double NaiveBayes::computeStandardDeviation(vector arr) {

    double sum = 0;

    double ave = computeMean(arr);
    for (int i = 0; i < arr.size(); i++) {
        sum += pow(arr[i] - ave, 2);
    }
    return sqrt(sum / (arr.size() - 1));
}

void NaiveBayes::computeNormalDistributionParameter() {
    for (int i = 1; i <= 3; i++) {
        //每一类遍历一次
        for (int j = 1; j < data[i].size(); j++) {
            //每一类的每一个成分遍历一次
            vector arr;
            arr.resize(13);
            //每个成分竖着遍历一次
            for (int k = 0; k < data.size(); k++) {
                if (data[k][0] == i) {
                    arr.push_back(data[k][j]);
                }
            }
            node tmp(computeMean(arr), computeStandardDeviation(arr));
            normalDistributionParameter[i - 1][j - 1] = tmp;
        }
    }

}

double NaiveBayes::gaussianDistribution(double num, double ave, double standardDeviation) {

    return exp(pow(num - ave, 2) / (-2 * pow(standardDeviation, 2))) * pow((sqrt(2 * M_PI) * standardDeviation), -1);
}

void NaiveBayes::NaiveBayesClassifier(vector posteriorProbability) {
    int max = 0;
    for (int i = 0; i < posteriorProbability.size(); i++) {

        if (posteriorProbability[max] < posteriorProbability[i]) {
            max = i;
        }
        cout << "此酒为类型" << i + 1 << "的概率为：   " << posteriorProbability[i] << '\n';
    }
    cout << "此酒为类型应为：" << max + 1 << '\n';
}

vector NaiveBayes::computePosteriorProbability(vector sample) {
    vector posteriorProbability;
    posteriorProbability.resize(normalDistributionParameter.size());
    for (int i = 0; i < posteriorProbability.size(); i++) {
        double probability = prioriProbability[i];
        for (int j = 0; j < normalDistributionParameter[i].size(); j++) {
            probability *= gaussianDistribution(sample[j], normalDistributionParameter[i][j].mean,
                                                normalDistributionParameter[i][j].standardDeviation);

        }
        posteriorProbability[i] = probability;
        /*
         * push_back()会增加 size ，导致越界
         */
    }
    return posteriorProbability;
}


int main() {

    NaiveBayes test("/Users/*************/Desktop/人工智能导论/实验/wine.data");
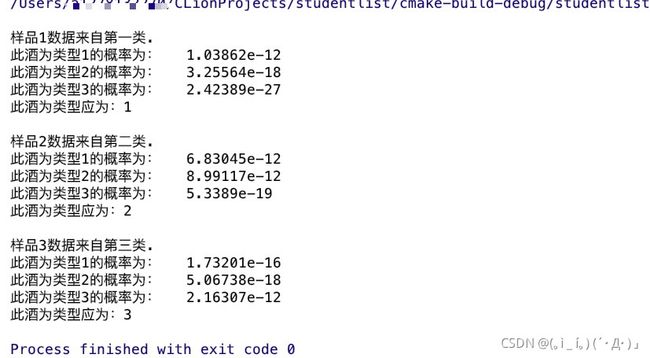
    cout << "\n样品1数据来自第一类.\n";
    vector sample1 = {14.2, 1.76, 2.45, 15.2, 112, 3.27, 3.39, .34, 1.97, 6.75, 1.05, 2.85, 1450};
    test.NaiveBayesClassifier(test.computePosteriorProbability(sample1));

    cout << "\n样品2数据来自第二类.\n";
    vector sample2 = {12.72, 1.81, 2.2, 18.8, 86, 2.2, 2.53, .26, 1.77, 3.9, 1.16, 3.14, 714};
    test.NaiveBayesClassifier(test.computePosteriorProbability(sample2));

    cout << "\n样品3数据来自第三类.\n";
    vector sample3 = {14.13, 4.1, 2.74, 24.5, 96, 2.05, .76, .56, 1.35, 9.2, .61, 1.6, 560};
    test.NaiveBayesClassifier(test.computePosteriorProbability(sample3));

    return 0;
}

五、实验结果