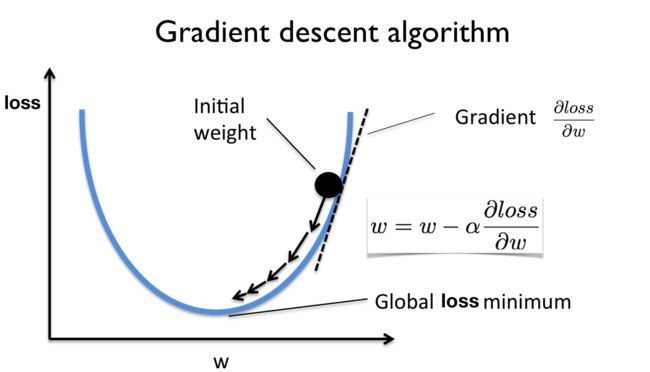
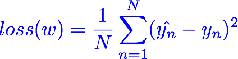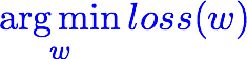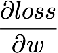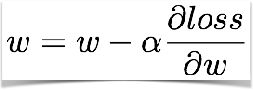梯度下降算法:
待优化的损失值为 loss,那么我们希望预测的值能够很接近真实的值 y_pred ≈ y_label
我们的样本有n个,那么损失值可以由一下公式计算得出:
要使得loss的值尽可能的小,才会让预测的值接近于标签值:
这里 arg 是(argument的缩写),数学中我们常常会遇到求最大最小值问题,通常会用argmax(F)、argmin(F)来求F函数的极值。
上述公式中的argmin就是去求我们的loss的最小值的w的参数的。
那么问题来了,argmin使用什么方式来去优化我们的F函数呢?
梯度下降优化算法:(梯度下降顾名思义就是根据梯度来优化我们的loss使其减小的)
这里涉及到基本的微分思想(求偏导数)
Y = W × X
dY/dX的值等于W, dY/dW的值为X
step1 : 求出loss的梯度值
step2: 更新W的值(迭代使得loss最小)
我们来看一下python的代码(手动求导):
x_data = [1.0, 2.0, 3.0] y_data = [2.0, 4.0, 6.0] w = 1.0 # a random guess: random value # our model forward pass def forward(x): return x * w # Loss function def loss(x, y): y_pred = forward(x) return (y_pred - y) * (y_pred - y) # compute gradient (计算梯度的值) def gradient(x, y): # d_loss/d_w return 2 * x * (x * w - y) # Before training print("predict (before training)", 4, forward(4)) # Training loop for epoch in range(10): for x_val, y_val in zip(x_data, y_data):
#计算梯度 grad = gradient(x_val, y_val) # 更新W的值,0.01是学习率,换个意思就是w每次更新的步长是多少
w = w - 0.01 * grad print("\tgrad: ", x_val, y_val, round(grad, 2)) l = loss(x_val, y_val) print("progress:", epoch, "w=", round(w, 2), "loss=", round(l, 2)) # After training print("predict (after training)", "4 hours", forward(4))
#控制台输出的结果
predict (before training) 4 4.0
grad: 1.0 2.0 -2.0
grad: 2.0 4.0 -7.84
grad: 3.0 6.0 -16.23
progress: 0 w= 1.26 loss= 4.92
grad: 1.0 2.0 -1.48
grad: 2.0 4.0 -5.8
grad: 3.0 6.0 -12.0
progress: 1 w= 1.45 loss= 2.69
grad: 1.0 2.0 -1.09
grad: 2.0 4.0 -4.29
grad: 3.0 6.0 -8.87
progress: 2 w= 1.6 loss= 1.47
grad: 1.0 2.0 -0.81
grad: 2.0 4.0 -3.17
grad: 3.0 6.0 -6.56
progress: 3 w= 1.7 loss= 0.8
grad: 1.0 2.0 -0.6
grad: 2.0 4.0 -2.34
grad: 3.0 6.0 -4.85
progress: 4 w= 1.78 loss= 0.44
grad: 1.0 2.0 -0.44
grad: 2.0 4.0 -1.73
grad: 3.0 6.0 -3.58
progress: 5 w= 1.84 loss= 0.24
grad: 1.0 2.0 -0.33
grad: 2.0 4.0 -1.28
grad: 3.0 6.0 -2.65
progress: 6 w= 1.88 loss= 0.13
grad: 1.0 2.0 -0.24
grad: 2.0 4.0 -0.95
grad: 3.0 6.0 -1.96
progress: 7 w= 1.91 loss= 0.07
grad: 1.0 2.0 -0.18
grad: 2.0 4.0 -0.7
grad: 3.0 6.0 -1.45
progress: 8 w= 1.93 loss= 0.04
grad: 1.0 2.0 -0.13
grad: 2.0 4.0 -0.52
grad: 3.0 6.0 -1.07
progress: 9 w= 1.95 loss= 0.02
predict (after training) 4 hours 7.804863933862125