变分自编码器(VAE)编程实现
一、简介
本文使用VAE的方法去学习MNIST手写数字图像。
使用的是Pytorch深度学习框架。
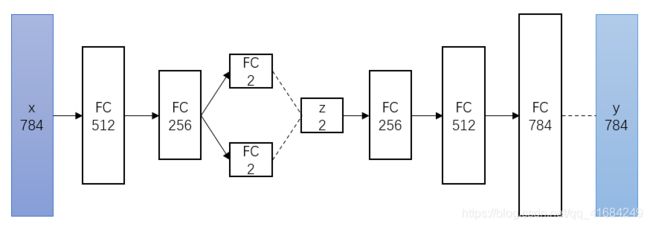
MNIST手写数字图像大小是1×28×28,将其展平为一个784维向量,这个向量就是输入x。
然后经过编码器得到潜在空间的特征。编码器由全连接层组成。首先经过一个512维的全连接层,然后经过一个256维的全连接层,最后分别经过一个2维的全连接层,得到潜在特征的均值和方差。
再次将编码器得到的均值和方差通过公式变换得到二维的潜在特征z。
最后通过解码器得到由z生成的图像y。解码器由全连接层组成。首先经过一个256维的全连接层,然后经过一个512维的全连接层,最后经过一个784维的全连接层得到生成的图像y。
我们的目的是生成的图像y和输入图像x是近似相同的,越越相似越好。
二、编程实现
根据上述写VAE模型。
import torch
import torch.nn as nn
class VAE(nn.Module):
def __init__(self, x_dim, h_dim1, h_dim2, z_dim):
super(VAE, self).__init__()
# 编码器
self.fc1 = nn.Linear(x_dim, h_dim1)
self.fc2 = nn.Linear(h_dim1, h_dim2)
self.fc31 = nn.Linear(h_dim2, z_dim)
self.fc32 = nn.Linear(h_dim2, z_dim)
# 解码器
self.fc4 = nn.Linear(z_dim, h_dim2)
self.fc5 = nn.Linear(h_dim2, h_dim1)
self.fc6 = nn.Linear(h_dim1, x_dim)
# 编码器
def encoder(self, x):
h = nn.ReLU()(self.fc1(x))
h = nn.ReLU()(self.fc2(h))
return self.fc31(h), self.fc32(h)
# 换算z的公式
def sampling(self, mu, log_var):
std = torch.exp(0.5 * log_var)
eps = torch.randn_like(std) # 生成std形状大小的随机标准正态分布的噪声
return eps.mul(std).add_(mu) # 得到z
# 解码器
def decoder(self, z):
h = nn.ReLU()(self.fc4(z))
h = nn.ReLU()(self.fc5(h))
return nn.Sigmoid()(self.fc6(h))
def forward(self, x):
mu, log_var = self.encoder(x.view(-1, 784))
z = self.sampling(mu, log_var)
return self.decoder(z), mu, log_var
写测试程序。我是用多gpu进行训练,当然可以修改为使用单个gpu训练,或者使用cpu训练。
import os
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
from torchvision import datasets, transforms
from vae import VAE
import torch.nn.functional as F
# 设置gpu
os.environ['CUDA_VISBLE_DEVICES'] = '0, 1'
# 数据集预处理
transforms = transforms.Compose([
transforms.ToTensor()
])
# 下载数据集
trainDataset = datasets.MNIST(root='./mnist_data/', train=True, transform=transforms, download=True)
testDataset = datasets.MNIST(root='./mnist_data/', train=False, transform=transforms, download=False)
# 加载数据集
trainLoader = torch.utils.data.DataLoader(dataset=trainDataset, batch_size=128, shuffle=True, num_workers=8)
testLoader = torch.utils.data.DataLoader(dataset=testDataset, batch_size=128, shuffle=False, num_workers=8)
# 创建模型
vae = VAE(784, 512, 256, 2)
if torch.cuda.is_available():
vae = nn.DataParallel(vae)
vae.cuda()
# 优化
optimizer = torch.optim.SGD(vae.parameters(), lr=1e-4, weight_decay=5e-4)
# 损失函数
def lossFunction(recon_x, x, mu, log_var):
bce = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')
kld = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
return bce + kld
# 训练函数
def train(epoch):
vae.train()
for batch_idx, (data, _) in enumerate(trainLoader):
data = data.cuda()
recon_batch, mu, log_var = vae(data)
loss = lossFunction(recon_batch, data, mu, log_var)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch_idx % 128 == 0:
print('Train Epoch: {} [{}/{} ({:0f}%)]\tLoss: {:.6f}'.format(epoch, batch_idx * len(data),
len(trainLoader.dataset), 100. * batch_idx / len(trainLoader), loss.item() / len(data)))
# 测试函数
def test():
vae.eval()
testLoss = 0
with torch.no_grad():
for data, _ in testLoader:
data = data.cuda()
recon, mu, log_var = vae(data)
testLoss += lossFunction(recon, data, mu, log_var).item()
testLoss /= len(testLoader.dataset)
print('=====> Test set loss: {:.4f}'.format(testLoss))
# 训练
for epoch in range(500):
train(epoch)
test()
# 潜在变量z通过解码器生成图片
with torch.no_grad():
n = 20
digitSize = 28
figure = np.zeros((digitSize * n, digitSize * n))
gridX = np.linspace(-4, 4, n)
gridY = np.linspace(-4, 4, n)
for i, xi in enumerate(gridX):
for j, yi in enumerate(gridY):
zSample = torch.Tensor([[yi, xi]]).cuda()
xDecoder = vae.module.decoder(zSample).cuda()
digit = xDecoder[0].cpu().detach().numpy().reshape(digitSize, digitSize)
figure[(n-i-1)*digitSize: (n-i) * digitSize, j*digitSize:(j+1) *digitSize] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure)
plt.savefig("Result")
plt.show()
三、实验结果
最后对训练的模型进行测试。潜在特征是个二维向量,即只有两个数。我们通过给不同的z来生成图像。
如图是实验的结果。横纵坐标分别代表潜在特征z的二维向量的其中一个值。最后发现,同一个数字的图像,潜在特征z的值是相近的。
同一个数字的图像在潜在空间上是聚集在一起的。