变分自编码器（VAE）（一）

前言

说来惭愧，VAE接触很久了，一直想把VAE好好的总结一下，一直拖到现在。

闲话少说，关于VAE的文章网上也有不少，解释的最好最清楚的还是苏剑林老师的这篇文章文章链接，还有B站白板推导系列中关于变分推断跟变分自编码器链接。大家可以多看看这两个资料，或者直接看我这次的总结肯定也不错的。

---

一、理解VAE前需要了解的知识点

1.极大似然估计

关于极大似然估计可以看我这篇文章，理解极大似然估计的原理，因为VAE中也用到了极大似然估计的原理。https://blog.csdn.net/zeronose/article/details/122437636?spm=1001.2014.3001.5501https://blog.csdn.net/zeronose/article/details/122437636?spm=1001.2014.3001.5501

2.高斯混合模型（GMM）

理解高斯混合模型主要是想让GMM跟VAE进行对比，更容易理解，因为GMM和VAE都属于是隐变量模型，其中都有隐变量这个概念。

这篇之前的文章是介绍EM算法的，里面的例子就是用EM算法去解决高斯混合模型的参数估计问题。可以通过这篇文章来理解高斯混合模型。https://blog.csdn.net/zeronose/article/details/122465732?spm=1001.2014.3001.5501https://blog.csdn.net/zeronose/article/details/122465732?spm=1001.2014.3001.5501

3.变分推断

变分推断是想办法找到一个分布去逼近无法计算得出解析解的后验分布。这也是VAE中用来求解后验分布的方法。可以看B站白板推导关于变分推断部分https://www.bilibili.com/video/BV1aE411o7qd?spm_id_from=333.999.0.0https://www.bilibili.com/video/BV1aE411o7qd?spm_id_from=333.999.0.0

二、AE的基本认识

这里的图全部来源于网络，侵权必删，其中下面关于月亮的一部分，来源于这篇文章，侵权必删。

这篇文章也非常的不错http://www.gwylab.com/note-vae.htmlhttp://www.gwylab.com/note-vae.html

AE就是自动编码器，VAE是在AE的基础上来的，所以这里先介绍一下AE。 

先看一下下面两个图：

如上面两个图所示，AE主要有encoder和decoder两个部分组成，其中encoder和decoder都是神经网络。其中encoder负责将高维输入转换为低维的code，decoder负责将低维的code转换为高维的输入，其中输出要跟输入尽可能的相似，最好是能完全一样。

看第二个图的中间部分，就代表了code，我们经过训练，最终得到了一个6维的code，且每个维度有一个具体的值代表。因为AE就是想生成跟输入相同的图像，所以AE是不会产生新的图像的，就像上面第二个图，最后生成的这个大叔，不会是一个闭嘴不笑，红头发的大叔。

再举一个例子，如下图：

如上图，经过训练我们的AE已经能还原这两张图片。接下来，我们在code空间上，两张图片的编码点中间处取一点，然后将这一点交给解码器，我们希望新的生成图片是一张清晰的图片（类似3/4全月的样子）。但是，实际的结果是，生成图片是模糊且无法辨认的乱码图。

为什么我们在code的中间取一点，无法生成3/4月亮的图呢？？？？

还是因为，AE就是要生成跟输入尽可能相同的图，类似与压缩与解压缩的过程，你想让AE生成一个相似但全新的图，它是做不到的。

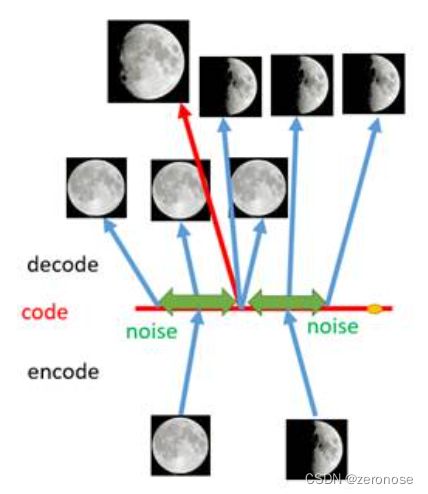
那如果我就是想生成3/4月亮的图怎么办？有一种方法，我们可以引入噪声，使得图片的编码区域得到扩大，从而掩盖掉失真的空白编码点。如下图所示：

如上图所示，现在在给两张图片编码的时候加上一点噪音，使得每张图片的编码点出现在绿色箭头所示范围内，于是在训练模型的时候，绿色箭头范围内的点都有可能被采样到，这样解码器在训练时会把绿色范围内的点都尽可能还原成和原图相似的图片。然后我们可以关注之前那个失真点，现在它处于全月图和半月图编码的交界上，于是解码器希望它既要尽量相似于全月图，又要尽量相似于半月图，于是它的还原结果就是两种图的折中（3/4全月图）。

由此我们发现，给编码器增添一些噪音，可以有效覆盖失真区域。不过这还并不充分，因为在上图的距离训练区域很远的黄色点处，它依然不会被覆盖到，仍是个失真点。为了解决这个问题，我们可以试图把噪音无限拉长，使得对于每一个样本，它的编码会覆盖整个编码空间，不过我们得保证，在原编码附近编码的概率最高，离原编码点越远，编码概率越低。在这种情况下，图像的编码就由原先离散的编码点变成了一条连续的编码分布曲线，如下图所示。

那么上述的这种将图像编码由离散变为连续的方法，就是变分自编码的核心思想。VAE中间的code不是具体的值，而是一种分布。如下图所示：

三、VAE的基本认识

上面介绍完了AE，接着就来介绍一下VAE。VAE是从AE的基础上来的，其中我们知道，AE类似于一种压缩解压缩的过程，只能生成与输入图像尽可能一样的图像，而不会生成与输入图像相似但不同的图像，这是AE本身所限制的。在这个基础上，VAE中间的code是一个分布，从分布中采样然后输入到decoder中，VAE可以生成与输入图像相似但不同的图像。

如下图所示，为VAE的基本结构图：

如下图所示，为VAE原文中给出的VAE的图模型，从VAE的图模型我们可以看到，z是服从标准正太分布的。

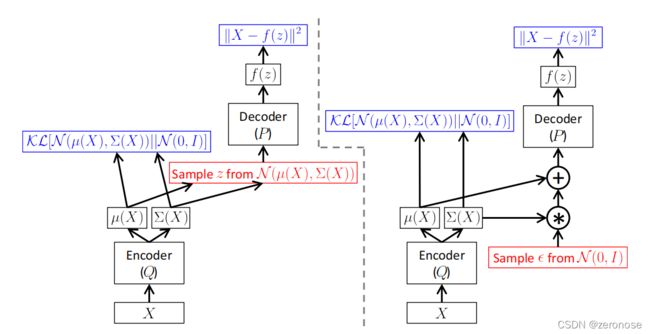
如下图所示，为VAE原文中给出的VAE的结构图。其中分为左右两个部分，右边才是最终的VAE结构。右边比左边就多了一个从标准正太分布中采样的过程，称为重参数化技巧，后面会说到为什么要有这个重参数化技巧。

感觉东西有点多，一篇文章写下来比较臃肿，大家看到后面会没有兴趣，所以将VAE分为（一）、（二）两个部分去介绍，（二）会介绍如下内容：

三、VAE公式推导

四、补充说明

 （二）部分是重中之重，理解了公式的推导，基本上就算彻底理解了VAE。https://blog.csdn.net/zeronose/article/details/122660359

​​​​​​​

​​​​​​​