多普勒频移测速与FMCW测距
文章目录
- 参考论文
- 时域与频域
- 基于多普勒频移估计速度
- 基于传统的FMCW测距
-
- 什么是FMCW
- FMCW测距原理
- 改进的FMCW
-
- 1、使用FMCW相位测距(手机是发送方)
-
- 传统FMCW方法在峰值估计上的错误
- 使用FMCW相位
- 2、分布式FMCW(手机是接收方)
-
- Step1:在接收信号上进行一次近似同步
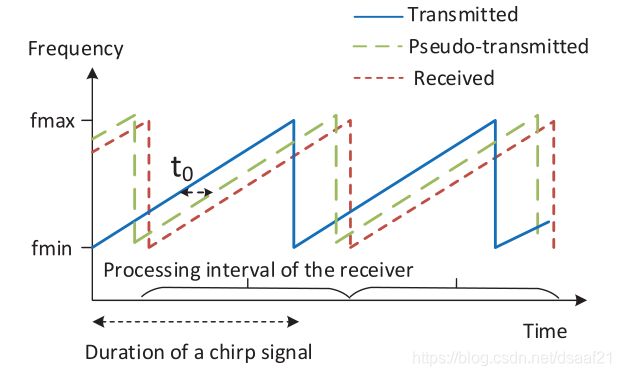
- Step2:引入pseudo-transmission time
- Step3:估计参考点
- Step4:考虑接收方运动的影响
- Step5:考虑频率偏移
- Step6:优化框架,得到最合适的移动方坐标
该博客是在学习利用FMCW原理进行声源信号追踪过程中的学习笔记。
参考论文
- CAT: High-Precision Acoustic Motion Tracking
- Vernier: Accurate and Fast Acoustic Motion Tracking Using Mobile Devices
- MilliSonic: Pushing the Limits of Acoustic Motion Tracking
- Turning a Mobile Device into a Mouse in the Air
相关部分已经更新到另一篇博客:点击链接
时域与频域
时域 — 自变量是时间,即横轴是时间,纵轴是信号振幅的变化。表示振幅随时间的变化。
频域 — 自变量是频率,即横轴是频率,纵轴是该频率信号幅度的峰值。表示振幅峰值随频率的变化。
基于多普勒频移估计速度
当发送端静止而接收端相对运动时,有:
- v = F s F c v=\frac{F^s}{F}c v=FFsc
其中,F是信号的原始频率; F s F^s Fs 是接收信号频率与发送信号频率之差,即多普勒频移;c是声波的传播速度;v是接收源相对发送源的移动速度。
因此,通过测量 F s F_s Fs ,我们就能估计接收端的速度 v 了,这时我们使用STFT(短时傅里叶变换)获得 F s F_s Fs
短时傅里叶变换:采用滑动窗口机制,设定窗口(窗函数,例如汉宁窗)大小和步长,让窗口在时域信号上滑动,分别计算每个窗口的傅立叶变换,形成了不同时间窗口对应的频域信号,拼接起来就成为了频率随时间变化的数据(时频信号)。加窗在时域上表现的是点乘,因此在频域上则表现为卷积。
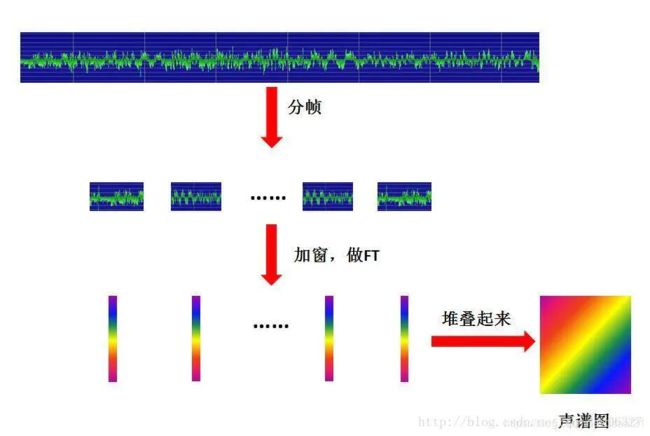
计算得到的速度的误差由公式 F = F s L w F^=\frac{F_s}{L_w} F=LwFs 决定,其中: L w L_w Lw 是窗口的长度, F s F_s Fs 是采样率
基于传统的FMCW测距
什么是FMCW
每个 FMCW 都是由若干个相同的 chirp组成,每个 chirp 是一组声波频率按固定斜率变化的声波,如下图:
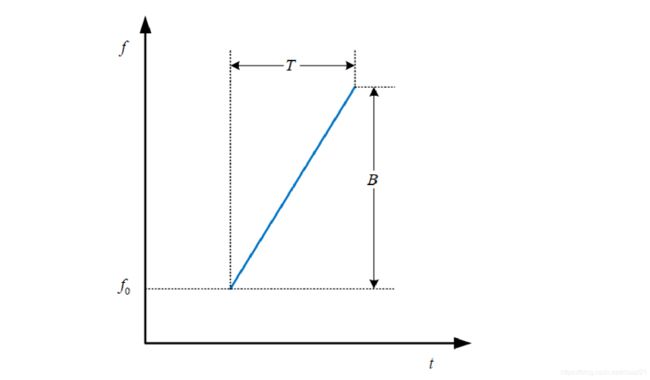
每个chirp周期内,频率线性地从fmin增加到fmax,频率 f ( t ) = f m i n + B t T f(t)= f_{min} + \frac{Bt}{T} f(t)=fmin+TBt,其中B为信号的带宽( B = f m a x − f m i n B=f_{max}-f_{min} B=fmax−fmin),T为信号的周期
将若干个 chirp 连接在一起就是 FMCW,如下图:
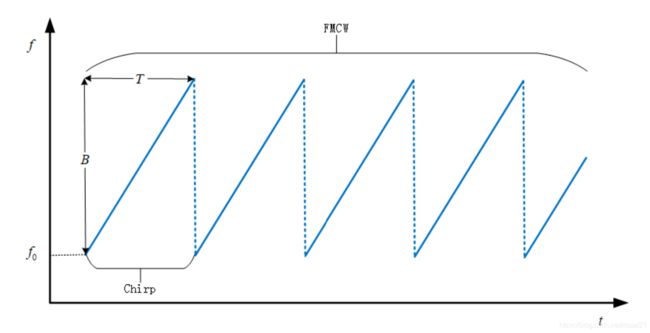
因为 FMCW 信号是由多个 Chirp 信号组合而成的周期信号,所以FMCW 的频率为:
- f ( t ) = f m i n + B T ( t − n T ) f(t) = f_{min} +\frac{B}{T} (t − nT) f(t)=fmin+TB(t−nT)
FMCW测距原理

根据频率是相位的微分,相位是频率的积分,又每个chirp的频率为: f ( t ) = f m i n + B t T f(t)= f_{min} + \frac{Bt}{T} f(t)=fmin+TBt
对频率按时间积分可得相应的相位: u ( t ) = 2 π ( f m i n t + B t 2 2 T ) u(t) = 2π(f_{min}t + B\frac{t^2}{2T} ) u(t)=2π(fmint+B2Tt2)
在第n次扫描期间(即第n个chirp)传输的信号为: v t ( t ′ ) = c o s ( 2 π f m i n t ′ + π B t ′ 2 T ) v_t(t') =cos(2πf_{min}t' + \frac{πBt'^2}{T}) vt(t′)=cos(2πfmint′+TπBt′2),其中t’=t-nT
FMCW波在延迟 t d t_d td时间后传播到接收端,接收到的信号会衰减: v r ( t ′ ) = α c o s ( 2 π f m i n ( t ′ − t d ) + π B ( t ′ − t d ) 2 T ) v_r(t')= α cos(2πf_{min}(t' − t_d) + \frac{πB(t' − t_d)^2}{T}) vr(t′)=αcos(2πfmin(t′−td)+TπB(t′−td)2),其中 α为衰减系数
接收方将收到的信号和发送的信号混合, v m ( t ) = v r ( t ) v t ( t ) v_m(t) = v_r(t)v_t(t) vm(t)=vr(t)vt(t);利用cos A cos B = (cos(A − B) + cos(A + B))/2,并过滤掉高频部分cos(A + B),得:
- v m ( t ) = α c o s ( 2 π f m i n t d + π B ( 2 t ′ t d − t d 2 ) T ) v_m(t) = α cos(2πf_{min}t_d + πB\frac{(2t't_d − t_d^2)}{T}) vm(t)=αcos(2πfmintd+πBT(2t′td−td2))
假设发送方与接收方相距R,发送方以v的速度移动, t d = R + v t ′ c t_d=\frac{R+vt'}{c} td=cR+vt′,带入上式得:
- α c o s ( 2 π f m i n R + v t ′ c + ( 2 π B t ′ ( R + v t ′ ) c T − π B ( R + v t ′ ) 2 c 2 T ) ) α cos(2πf_{min} \frac{R + vt'}{c} + (\frac{2πBt'(R + vt')}{cT}− \frac{πB(R + vt')^2}{c^2T})) αcos(2πfmincR+vt′+(cT2πBt′(R+vt′)−c2TπB(R+vt′)2))
将上式中的相位部分对 t ′ t' t′ 求导,常数项可以忽略,关于 1 c 2 {\frac1c}^{2} c12的二次项太小,也可以忽略,t’的平均值为T/2,得到:
- f p = 1 2 π δ P h a s e δ t ′ = B R c T + f m i n v c + B v c f_p = \frac1{2π}\frac{δPhase}{δt'} = \frac{BR}{cT} + \frac{f_{min}v}{c}+ \frac{Bv}{c} fp=2π1δt′δPhase=cTBR+cfminv+cBv
当v接近于0时,频谱的第一个峰值为 B R c T \frac{BR}{cT} cTBR
如果发送方和接收方之间存在多路径传播,在混合信号的频谱中观察到多个峰值,在这种情况下 f p f_p fp 由第一个峰值决定,该峰值对应于直接路径。通过测量第一个峰值 f p f_p fp ,距离 R = f p c T B R=\frac {f_pcT}{B} R=BfpcT
改进的FMCW
1、使用FMCW相位测距(手机是发送方)
传统FMCW方法在峰值估计上的错误
直接路径的到达时间为 t 1 t_1 t1,对应解调信号的频率为 f t 1 f_{t_1} ft1;非直接路径的到达时间为 t 2 t_2 t2,对应解调信号的频率为 f t 2 f_{t_2} ft2。
当 ∣ f t 1 − f t 2 ∣ < 1 |f_{t_1}-f_{t_2}|<1 ∣ft1−ft2∣<1时,两个峰值在频域内合并成为一个峰值,近似于 ( A 2 f t 2 + A 1 f t 1 ) / ( A 2 + A 1 ) (A_2f_{t_2}+A_1f_{t_1})/(A_2+A_1) (A2ft2+A1ft1)/(A2+A1),其中A1和A2分别是直接路径的振幅和剩余非直接路径的总振幅,因此频率的错误为 ( A 2 f t 2 + A 1 f t 1 ) / ( A 2 + A 1 ) − f t 1 = ( f t 2 − f t 1 ) / ( 1 + A 1 A 2 ) (A_2f_{t_2}+A_1f_{t_1})/(A_2+A_1)-f_{t_1}=(f_{t_2} − f_{t_1})/(1 + \frac{A_1}{A_2} ) (A2ft2+A1ft1)/(A2+A1)−ft1=(ft2−ft1)/(1+A2A1)
随( f t 2 − f t 1 f_{t_2} − f_{t_1} ft2−ft1)线性增长,并且随着 A 1 A 2 \frac{A_1}{A_2} A2A1按比例增长
使用FMCW相位
方法:
1) 在时域应用动态窄带带通滤波器来滤除大部分到达时间较远的多径,这使得我们只剩下了直接路径周围剩余的一小部分间接路径。
2) 从瞬时FMCW相位提取距离信息(具体怎么从相位中获取距离信息论文没提)。
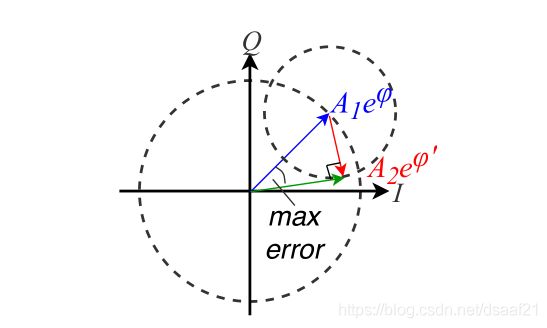
假设在通过滤波器后,剩余的非直接路径的振幅比直接路径的振幅低。蓝色向量:直接路径;红色向量:所有剩下的非直接路径之和;绿色向量:前两个向量之和。
因此,最大相位错误发生在红色向量垂直于绿色向量时,相位错误为 s i n − 1 ( A 2 A 1 ) sin^{-1}(\frac{A_2}{A_1}) sin−1(A1A2),在 s i n − 1 ( A 2 A 1 ) sin^{-1}(\frac{A_2}{A_1}) sin−1(A1A2)处要增长得慢得多
2、分布式FMCW(手机是接收方)
在传统的FMCW中,发送方和接收方是在一起的并且分享同一个时钟;而在分布式FMCW中,发送方(扬声器)和接收方(麦克风)是分离的和不同步的。因此,传统FMCW中所需的传输时间对于接收方来说是未知的。
分布式FMCW使用如下步骤解决上述问题:
1)找到一个参考点并获知它的绝对位置
2)当发送方移动时,估计它相对于参考点的距离变化
3)推测出发送方和接收方的绝对距离
此时,就无需知道信号的传输时间了,但是,分离的接收方和发送方有不同的采样率
Step1:在接收信号上进行一次近似同步
如上图所示,近似同步保证每个处理周期都与单个chirp对齐,每次处理一个完整的chirp。
具体方法是将接收到的信号与原始chirp信号互相关(correlation),选择检测到最高相关峰的时间作为第一个处理周期的开始时间,同步只需要在开始时执行一次。
如上图,由于互相关通常会显示多个幅度相似的峰,因此同步是近似的。
Step2:引入pseudo-transmission time
由于在每个处理周期中,要将接收信号与发送信号混合,但是我们不知道发送信号开始的具体时间,因此,引入了pseudo-transmission time(接收方假设传输信号开始的时间,下图绿色虚线所示)
t0为第一个chirp中pseudo transmission time和实际发送时间之差,并且对于接收方来说是一个未知的常数,因此,在每个处理周期,估计距离相对于实际距离偏移一个常数:
R n = c T f n p B + c t 0 R_n=\frac{cTf_n^p}B+ct_0 Rn=BcTfnp+ct0
其中, R n R_n Rn为在第n个处理周期中发送方和接收方的距离, f n p f^p_n fnp是第n个处理周期中混合信号的峰值,c是声信号的传播速度,T是chirp的周期,B是信号带宽( B = f m a x − f m i n B=f_{max}-f_{min} B=fmax−fmin)。
根据上述等式,接着考虑两个处理周期:
R n − R 1 = ( f n p − f 1 p ) c T B R_n-R_1=(f_n^p-f_1^p)\frac{cT}B Rn−R1=(fnp−f1p)BcT
由于这个常数偏移,我们仅可以测量距离的变化量。要随时获取绝对距离,我们需要知道某个点(称为参考点)的绝对距离,并使用距离变化来获取新位置的绝对距离,即:
R n = ( f n p − f 1 p ) c T B + R 1 R_n=(f_n^p-f_1^p)\frac{cT}B+R_1 Rn=(fnp−f1p)BcT+R1
其中,R1就是参考点相对于扬声器的绝对距离
Step3:估计参考点
为了获得距离 R n R_n Rn,我们需要知道手机在某个点(称之为参考点)上与扬声器之间的绝对距离。
假设两个speaker分别位于(0,0)和(A,0)的位置,让移动设备沿x轴(两个扬声器之间的连线)来回移动。
当移动设备移动向speaker2时,它在接近speaker2并且在x=A之前,经历正多普勒频移;当经过x=A后,并且远离speaker2时,经历负多普勒频移。因此,我们可以检测到多普勒频移改变其符号的时间,并且那时移动设备移动到x = A上的一个点,就是我们的参考点。
假设参考点距离两个speaker的距离分别为D1和D2,我们可以通过让两个speaker相同时间开始发送信号并且使用相同的pseudo-transmission time(此时t0是相同的),然后使用FMCW测距D1与D2之差 Δ D \Delta D ΔD:
Δ D = D 1 − D 2 = c T ( f p , 1 − f p , 2 ) B \Delta D=D1-D2=\frac{cT(f_{p,1}-f_{p,2})}B ΔD=D1−D2=BcT(fp,1−fp,2)
又因为勾股定理: D 1 2 − D 2 2 = A 2 D1^2-D2^2=A^2 D12−D22=A2,我们可以得到D1和D2的值。
为了提高精度,我们可以多次扫描,让移动设备穿过参考位置多次,并将平均值用作为D1和D2的估计值。
Step4:考虑接收方运动的影响
为了简便,上述公式忽略了接收方运动的影响,但是不可忽略的速度会导致混合信号的峰值频率的额外频移。
因为 f p = B R c T + f m i n v c + B v c f_p = \frac{BR}{cT} + \frac{f_{min}v}{c}+ \frac{Bv}{c} fp=cTBR+cfminv+cBv,并且由于pseudo-transmission时间 t 0 t_0 t0,这个周期中的测量值与实际值 R n R_n Rn相差 c t 0 ct_0 ct0,因此得到下式:
- f n p = B ( R n − c t 0 ) c T + f m i n v n c + B v n c f_n^p=\frac{B(R_n-ct_0)}{cT}+\frac{f_{min}v_n}c+\frac{Bv_n}c fnp=cTB(Rn−ct0)+cfminvn+cBvn
其中, v n v_n vn是接收方相对于发送方在第n个处理周期的速度,为了简单,假设在第一个处理周期中是静止的(可以作为参考点)
- R n = ( f n p − f m i n v n c − B v n c − f 1 p ) c T B + R 1 R_n=(f_n^p-\frac{f_{min}v_n}c-\frac{Bv_n}c-f_1^p)\frac{cT}B+R_1 Rn=(fnp−cfminvn−cBvn−f1p)BcT+R1
根据上式,绝对距离 R n R_n Rn由第1个和第n个处理周期的峰值频率 f n p 、 f 1 p f_n^p、f_1^p fnp、f1p,基于多普勒频移的第n个处理周期接收方的速度 v n v_n vn,和参考点的距离 R 1 R_1 R1决定
Step5:考虑频率偏移
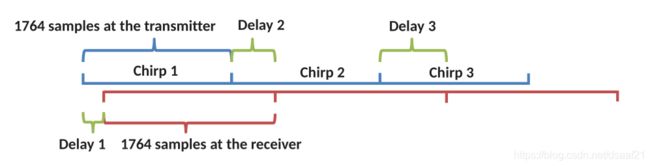
由于不完美的时钟,发送方和接收方的采样率不完全相同,也就是说发送方和接收方采样相同的点数花费不同的时间,因此也就引入的误差。
如上图,发送方传输一个由1764个采样点构成的chirp,在经历了Delay1的时间后,该chirp被接收方收到。由于接收器的时钟速率略有不同,因此接收器累积这1764个采样所需的时间稍长一些,所以Delay2不仅包括传输延迟还包括不同时钟速率造成的采样时间差。Delay3同理。
如果发送方和接收方是静态的,并且它们的采样率偏移是恒定的,则估计的延迟将随时间线性增加。为了补偿这种影响,我们在开始时引入了一个简短的校准阶段,我们会在校准过程中固定接收器的位置。
如果没有采样频率偏移,则FMCW检测到的峰值频率应固定,采样频率偏移将导致峰值频率随时间稳定变化,我们可以通过绘制随时间变化的峰值频率来估计偏移(对测量数据应用最小二乘拟合):
图中红虚线的斜率为k,我们按以下方式处理原始测量:
f p a d j u s t e d = f p r a w − k t f_p^{adjusted}=f_p^{raw}-kt fpadjusted=fpraw−kt
其中 f p a d j u s t e d f^{adjusted}_p fpadjusted和 f p r a w f_p^{raw} fpraw分别表示调整后的和原始的峰值频率,t是校准阶段经过的时间,k是拟合线的斜率
采样频率偏移可能会随时间缓慢变化,当接收器静止时,重新校准频率偏移。
Step6:优化框架,得到最合适的移动方坐标
结合了多普勒频移和FMCW测量,可进行精确的运动跟踪的优化框架:
∑ i ∈ [ k − n + 1.. k ] ∑ j α ( ∣ z i − c j ∣ − ∣ z 0 − c j ∣ − d F M C W i , j ) 2 + ∑ i ∈ [ k − n + 2.. k ] ∑ j β ( ∣ z i − c j ∣ − ∣ z i − 1 − c j ∣ − v i − 1 , j d o p p l e r T ) 2 \sum_{i\in [k-n+1..k]}\sum_j\alpha(|z_i-c_j|-|z_0-c_j|-d_{FMCW}^{i,j})^2+\\ \sum_{i\in [k-n+2..k]}\sum_j\beta(|z_i-c_j|-|z_{i-1}-c_j|-v_{i-1,j}^{doppler}T)^2 i∈[k−n+1..k]∑j∑α(∣zi−cj∣−∣z0−cj∣−dFMCWi,j)2+i∈[k−n+2..k]∑j∑β(∣zi−cj∣−∣zi−1−cj∣−vi−1,jdopplerT)2
其中,k是当前的处理周期,n是用于该优化的周期数, z i z_i zi表示在i个周期开始的时候移动方的位置, z 0 z_0 z0表示参考点的位置, c j c_j cj表示第j个周期扬声器的位置, d F M C W i , j d_{FMCW}^{i,j} dFMCWi,j表示在第i个周期中相对于第j个扬声器的参考点距离变化, v i , j d o p p l e r v_{i,j}^{doppler} vi,jdoppler表示在第i个周期中相对于第j个扬声器的速度。
优化框架反映了找到最适合FMCW和Doppler方法的移动方坐标,利用了多个周期来提高准确率。
第一项捕获基于坐标计算的距离应与从FMCW估计的距离相匹配,第二项捕获在从坐标计算的间隔内的行进距离应与从多普勒频移得出的距离相匹配。
上述的优化问题是非凸的,意味着不保证收敛并且计算开销大。上述公式中未知项为移动方的坐标,为了简化该问题,将移动方相对于扬声器的距离作为未知项,即将上述公式中的 ∣ z i − c j ∣ |z_i-c_j| ∣zi−cj∣替换成 D i , j D_{i,j} Di,j。