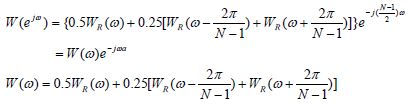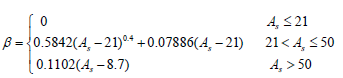fir数字滤波器设计与软件实现_数字与信号处理实验6 有限冲激响应(FIR)数字滤波器的设计...
实验六 有限冲激响应(FIR)数字滤波器的设计
一、实验要求
综合运用数字信号处理课程的理论知识进行频谱分析以及滤波器设计，通过理论推 导得出相应结论，并进行计算机仿真，从而复习巩固了课堂所学的理论知识，提高了对所学知识的综合应用能力。
二、实验原理
FIR滤波器的设计问题在于寻求一系统函数
，使其频率响应
逼近滤波器要求的理想频率响应
，其对应的单位脉冲响应
。
1．用窗函数设计FIR滤波器的基本方法
设计思想：从时域从发，设计
逼近理想
。设理想滤波器的单位脉冲响应为。以低通线性相位FIR数字滤波器为例。
一般是无限长的，且是非因果的，不能直接作为FIR滤波器的单位脉冲响应。要想得到一个因果的有限长的滤波器h(n)，最直接的方法是截断
，即截取为有限长因果序列，并用合适的窗函数进行加权作为FIR滤波器的单位脉冲响应。按照线性相位滤波器的要求，h(n)必须是偶对称的。对称中心必须等于滤波器的延时常数，即
用矩形窗设计的FIR低通滤波器，所设计滤波器的幅度函数在通带和阻带都呈现出振荡现象，且最大波纹大约为幅度的9%，这个现象称为吉布斯(Gibbs)效应。为了消除吉布斯效应，一般采用其他类型的窗函数。
2．典型的窗函数
(1)矩形窗(Rectangle Window)
其频率响应和幅度响应分别为： 
(2)三角形窗(Bartlett Window)
其频率响应为： 
(3)汉宁(Hanning)窗，又称升余弦窗
其频率响应和幅度响应分别为：
(4)汉明(Hamming)窗，又称改进的升余弦窗
其幅度响应为：
(5)布莱克曼(Blankman)窗，又称二阶升余弦窗
其幅度响应为：
(6)凯泽(Kaiser)窗
其中：β是一个可选参数，用来选择主瓣宽度和旁瓣衰减之间的交换关系，一般说来，β越大，过渡带越宽，阻带越小衰减也越大。I0(·)是第一类修正零阶贝塞尔函数。
若阻带最小衰减表示为
，β的确定可采用下述经验公式：
若滤波器通带和阻带波纹相等即δp=δs时，滤波器节数可通过下式确定： 
式中：
3．利用窗函数设计FIR滤波器的具体步骤如下：
(1)按允许的过渡带宽度△ω及阻带衰减AS，选择合适的窗函数，并估计节数N：
其中A由窗函数的类型决定。
(2)由给定的滤波器的幅频响应参数求出理想的单位脉冲响应。
(3)确定延时值
(4)计算滤波器的单位取样响应，。
(5)验算技术指标是否满足要求。
三、实验仪器
微型计算机、Matlab6.5 教学版、TC 编程环境。
四、实验内容
(1)编制能产生矩形窗、汉宁窗、汉明窗、三角形窗、布莱克曼窗和凯塞-贝塞尔窗 的窗函数子程序。
(2)编写主程序。用不同窗设计线性相位低通FIR 数字滤波器。观察3dB 和20dB 带 宽以及阻带最小衰减，比较四种窗函数对滤波特性的影响。
(3)对结果进行分析；
(4)完成实验报告。
五、实验结果
1、编制能产生矩形窗、汉宁窗、汉明窗、三角形窗、布莱克曼窗和凯塞-贝塞尔窗的子程序。
(1)编写amplres.m文件
function [Hw, w, type, tao] = amplres(h)
N = length(h); tao = (N - 1)/2;
L = floor((N - 1)/2);
n = 1 : L + 1; w = [0 : 1000] * 2 * pi/1000;
if all(abs(h(n) - h(N - n + 1)) < 1e-10)
Hw = 2 * h(n) * cos(((N + 1)/2 - n)' * w) - mod(N, 2) * h(L + 1);
type = 2 - mod(N, 2);
elseif all(abs(h(n) + h(N - n + 1)) < 1e-10)&&(h(L + 1) * mod(N, 2) == 0)
Hw = 2 * h(n) * sin(((N + 1)/2-n)' * w);
type = 4 - mod(N, 2);
else
error('错误，这不是线性相位FIR滤波器');
end
(2)利用amplres求四种线性相位FIR滤波器的幅度函数
。
1)在命令行窗口输入如下程序
h1 = [2, 1, -3, 5, 4, 5, -3, 1, 2]; h2 = [2, 1, -3, 5, 5, -3, 1, 2];
h3 = [2, 1, -3, 5, 0, -5, 3, -1, -2]; h4 = [2, 1, -3, 5, -5, 3, -1, -2];
[H1, w1, type, tao] = amplres(h1);
type1 = type, tao1 = tao,
subplot(221); plot(w1/pi, H1); grid
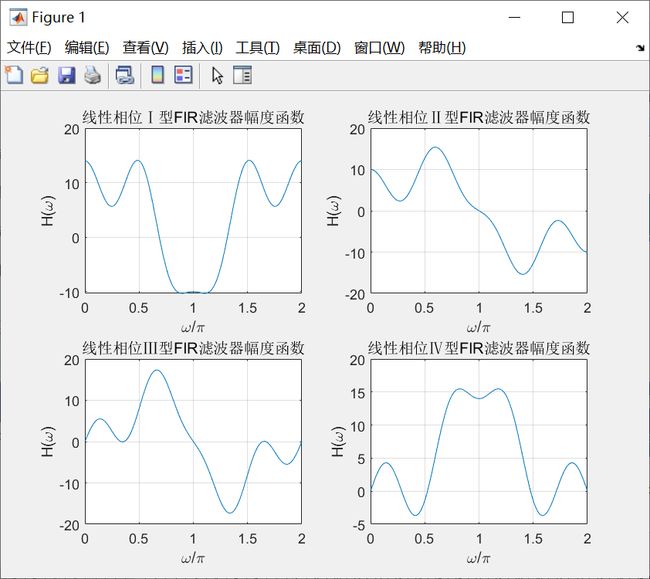
title('线性相位Ⅰ型FIR滤波器幅度函数');
xlabel('\omega/\pi'); ylabel('H(\omega)');
[H2, w2, type, tao] = amplres(h2);
type2 = type, tao2 = tao,
subplot(222); plot(w2/pi, H2); grid
title('线性相位Ⅱ型FIR滤波器幅度函数');
xlabel('\omega/\pi'); ylabel('H(\omega)');
[H3, w3, type, tao] = amplres(h3);
type3 = type, tao3 = tao,
subplot(223); plot(w3/pi, H3); grid
title('线性相位Ⅲ型FIR滤波器幅度函数');
xlabel('\omega/\pi'); ylabel('H(\omega)');
[H4, w4, type, tao] = amplres(h4);
type4 = type, tao4 = tao,
subplot(224); plot(w4/pi, H4); grid
title('线性相位Ⅳ型FIR滤波器幅度函数');
xlabel('\omega/\pi'); ylabel('H(\omega)');
2)得到如下图
2、编写主程序。用不同窗设计线性相位低通FIR 数字滤波器。观察3dB 和20dB 带宽以及阻带最小衰减，比较四种窗函数对滤波特性的影响。
(1)分别将如下代码写入命令行窗口
N = 33; wc = pi/4;
a = (N-1)/2;
n = 0:(N-1);
m = n - a + eps;
hdn = sin(wc*m)./(pi*m);
wn = boxcar(N);
hn = hdn.*(wn');
[H, w] = freqz(hn, [1], 1024, 'whole' );
dbH = 20 * log10((abs(H) + eps) / max(abs(H))) ;
figure(1); subplot(1,3,1);
stem(n, hn,'.');
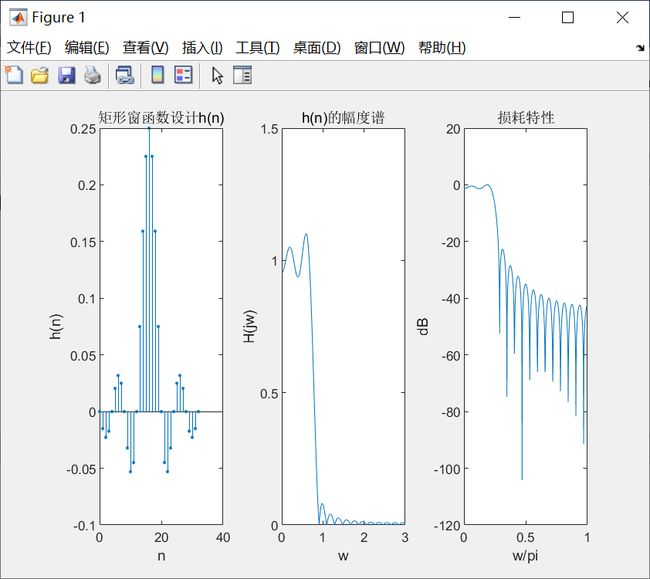
xlabel('n'); ylabel('h(n)' ); title('N=33时设计矩形窗h(n)');
subplot(1,3,2);
plot(w, abs(H));
xlabel('w'); ylabel('H(jw)'); title('h(n)的幅度谱'); axis([0,3,0,1.5]);
subplot(1,3,3);
plot(w/pi,dbH);
xlabel('w/pi'); ylabel('dB'); title('损耗特性'); axis([0, 1,20, 3]);
N = 33; wc = pi/4;
a = (N-1)/2;
n = 0:(N-1);
m = n - a + eps;
hdn = sin(wc*m)./(pi*m);
wn = hanning(N);
hn = hdn.*(wn');
[H, w] = freqz(hn, [1], 1024, 'whole' );
plot(w/pi, dbH);
xlabel('w/pi'); ylabel('dB' ); title('损耗特性'); axis([0, 1,-100, 0]);
dbH = 20 * log10((abs(H) + eps) / max(abs(H))) ;
figure(1); subplot(1,3,1);
stem(n, hn,'.');
xlabel('n'); ylabel('h(n)' ); title('汉宁窗函数设计h(n)');
subplot(1,3,2);
plot(w, abs(H));
xlabel('w'); ylabel('H(jw)'); title('h(n)的幅度谱'); axis([0,3,0,1.5]);
subplot(1,3,3);
plot(w/pi,dbH);
xlabel('w/pi'); ylabel('dB'); title('损耗特性'); axis([0, 1,20, 3]);
N = 33; wc = pi/4;
a = (N-1)/2;
n = 0:(N-1);
m = n - a + eps;
hdn = sin(wc*m)./(pi*m);
wn = hamming(N);
hn = hdn.*(wn');
[H, w] = freqz(hn, [1], 1024, 'whole' );
dbH = 20 * log10((abs(H) + eps) / max(abs(H))) ;
figure(1); subplot(1,3,1);
stem(n, hn,'.');
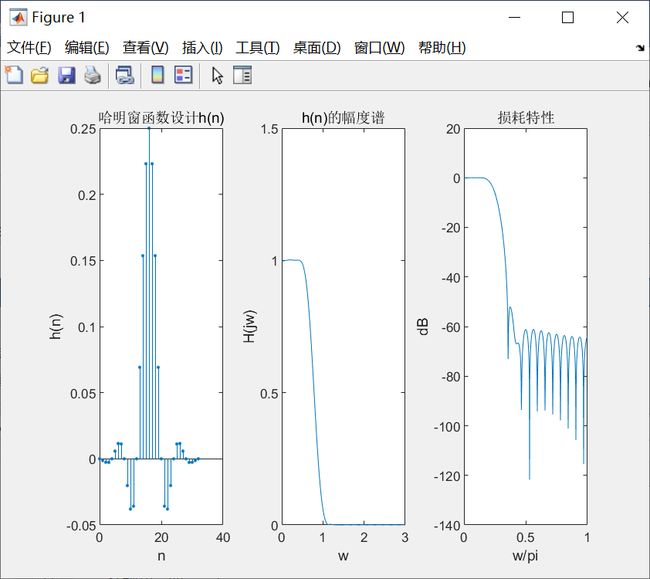
xlabel('n'); ylabel('h(n)' ); title('哈明窗函数设计h(n)');
subplot(1,3,2);
plot(w, abs(H));
xlabel('w'); ylabel('H(jw)'); title('h(n)的幅度谱'); axis([0,3,0,1.5]);
subplot(1,3,3);
plot(w/pi,dbH);
xlabel('w/pi'); ylabel('dB'); title('损耗特性'); axis([0, 1,20, 3]);
N = 33; wc = pi/4;
a = (N-1)/2;
n = 0:(N-1);
m = n - a + eps;
hdn = sin(wc*m)./(pi*m);
wn = blackman(N);
hn = hdn.*(wn');
[H, w] = freqz(hn, [1], 1024, 'whole' );
dbH = 20 * log10((abs(H) + eps) / max(abs(H))) ;
figure(1); subplot(1,3,1);
stem(n, hn,'.');
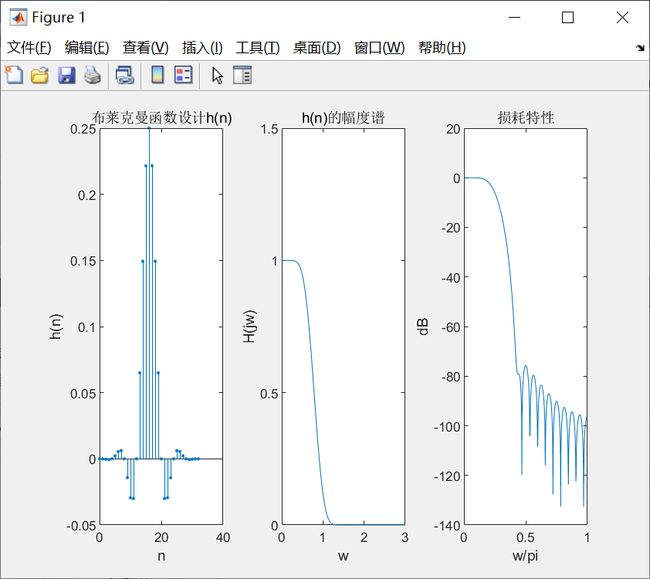
xlabel('n'); ylabel('h(n)' ); title('布莱克曼函数设计h(n)');
subplot(1,3,2);
plot(w, abs(H));
xlabel('w'); ylabel('H(jw)'); title('h(n)的幅度谱'); axis([0,3,0,1.5]);
subplot(1,3,3);
plot(w/pi,dbH);
xlabel('w/pi'); ylabel('dB'); title('损耗特性'); axis([0, 1,20, 3]);
(2)分别运行后得如下图
同一个窗函数，N值不同，过渡带的宽度不同，改善不了滤波器阻带的衰减。N的值大，斜率大，N的值小，斜率小。同一窗函数，不同的窗口长度，达到的阻带衰减是相同。
六、实验总结
通过本次实验我学会了用matlab编制能产生矩形窗、汉宁窗、汉明窗、三角形窗、布莱克曼窗和凯塞-贝塞尔窗的窗函数子程序，以及用不同窗设计线性相位低通FIR 数字滤波器程序；掌握了用matlab设计用不同窗设计线性相位低通FIR 数字滤波器程序；发现了自己在编程方面的不足；在今后的学习中，自己的编程能力有待提高。