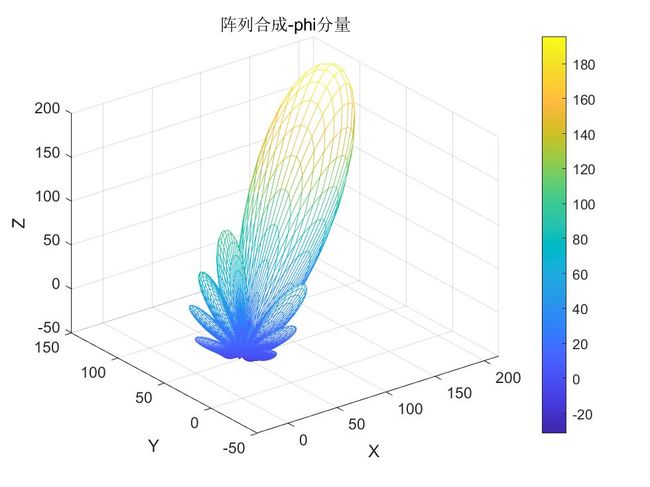
【Matlab应用】:相控阵天线方向图合成及波束扫描算法实现
阅读本文,你可能解决什么?
-
怎样由单天线仿真或测试的方向图,合成得到2D阵列的方向图?
-
怎样馈相实现阵列天线波束扫描?
-
怎样编程模拟方向图合成和波束扫描?
阅读本文,你可能收获什么?
-
Matlab编写的均匀平面阵列方向图合成及波束扫描的代码。
-
形象、直观的理解阵列天线的☆☆☆阵因子☆☆☆到底是什么?
各种基于实际应用的Matlab编程,可关注相关系列文章或回答。下链接也可直达本文。
(1 条消息) 如何利用matlab进行均匀线性阵列的仿真? - 知乎 (zhihu.com)![]() https://www.zhihu.com/question/392647576/answer/2441103022
https://www.zhihu.com/question/392647576/answer/2441103022
一、算法原理
1.1 阵列天线方向图合成
将单元天线组阵,可增强整体的方向性。控制阵列天线方向图的主要因素有4个:
-
单元方向图:
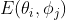 ,即随空间
,即随空间 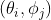 角变化的幅度和相位数据。可用复数矩阵表示
角变化的幅度和相位数据。可用复数矩阵表示 -
单元间距:
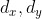
-
单元天线馈电幅度:
 (第 k 个单元天线馈电幅度)
(第 k 个单元天线馈电幅度) -
单元天线馈电相位:
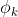 (第 k 个单元天线馈电相位)
(第 k 个单元天线馈电相位)
阵因子 (组阵可形象的理解为对单元方向图加了赋形窗)
阵列天线方向图的计算,并通过阵列中单个单元的远场乘以阵列的阵因子(Array Factor, AF )来得到。
设:每个天线为点源,组成M*N元的二维均匀平面阵,其中,X轴方向N个单元,间距![]() ,Y轴方向M个单元,间距
,Y轴方向M个单元,间距![]() ;单元天线馈电计为:
;单元天线馈电计为: ![]() ,则阵列天线的阵因子AF 为:
,则阵列天线的阵因子AF 为:
![]()
注:阵列因子AF取与单元方向图相同维度的数据,可视为给单元方向图赋形的窗函数
则M*N元的二维均匀平面阵合成的方向图 ![]() 有:
有:
![]()
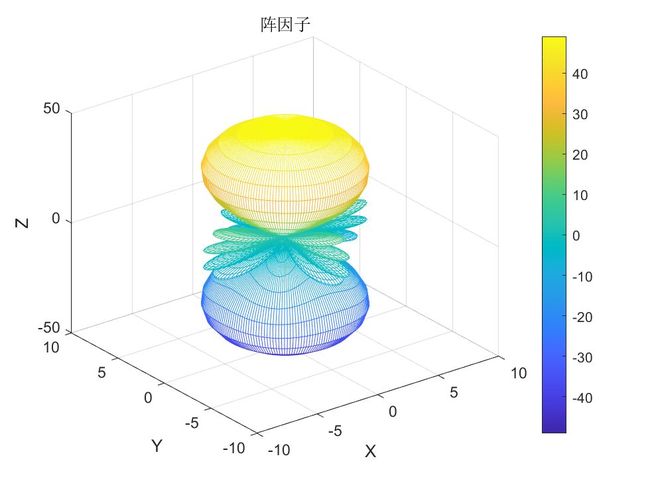
☆☆☆☆☆阵因子到底是什么?☆☆☆☆☆
一个编写程序才更深入理解的知识点。如下图所示某7*7阵列的阵因子。
某7*7阵列的阵因子
1.2 相控阵天线波束扫描
同样,以M*N元的二维均匀平面阵为例。
假设:X方向相邻单元之间馈电相位差为 ![]() , Y方向相邻单元之间馈电相位差为
, Y方向相邻单元之间馈电相位差为![]() 。
。
通过控制移相器改变![]() 和
和 ![]() 值,就可以实现阵列天线的波束扫描。
值,就可以实现阵列天线的波束扫描。
如需将波束指向空间的某个角度![]() ,则:
,则:
![]()
下面,对上述算法进行编程,并做验证。
首先,需仿真一个单元天线得到2D方向图数据,再假设组成的阵列,软件合成阵列方向图及波束扫描方向图;
其次,编写代码;
最后,跟软件仿真结果对比,验证代码的准确性。
二、仿真
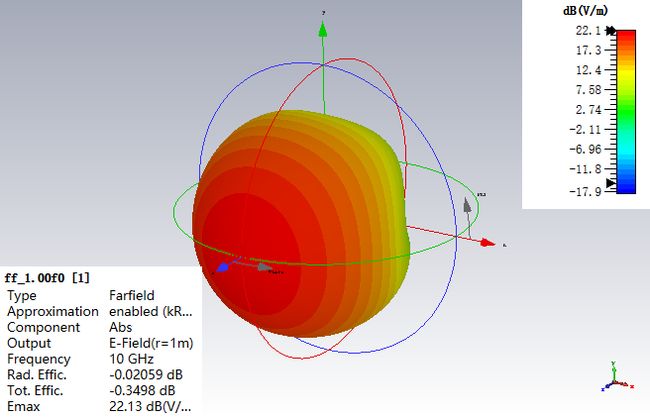
2.1 单元天线
可使用商业软件,仿真得到单元天线的方向图。
软件仿真-单元方向图
2.2 阵列方向图合成
假设组成7*7的均匀阵列,具体参数见代码行。采用软件进行仿真,结果示例如下。
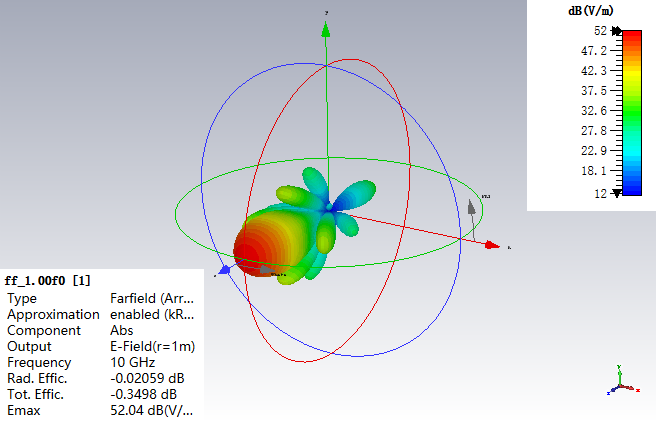
波束扫描角度:(0,0)
软件合成-3D-(0,0)
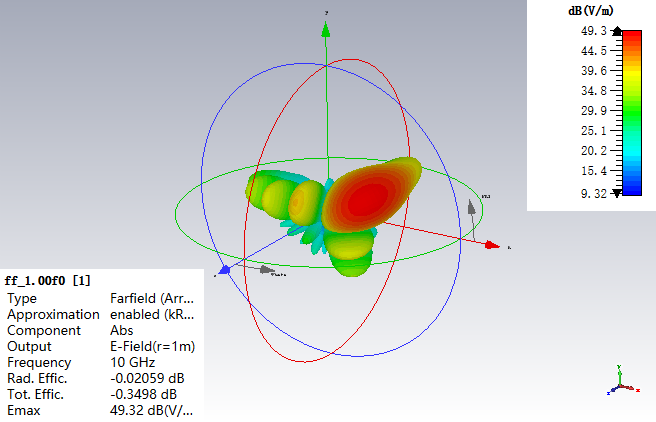
波束扫描角度:(60,30)
软件合成-3D-(60,30)
三、代码
画将2D方向图转化为3D方向图,非常有用的库函数。
sph2cart
将球面坐标转换为笛卡尔坐标。
语法
[x,y,z] =sph2cart(azimuth,elevation,r)示例
[x,y,z] = sph2cart(deg2rad(Phi),pi/2-deg2rad(Theta),FieldPlot);将球面坐标数组 Phi、Theta和 FieldPlot 的对应元素转换为笛卡尔坐标,即 xyz 坐标。其中,FieldPlot 为2D方向图的幅度(线性值)。
主函数
初步编写的方向图合成及波束扫描的代码如下。后续拟进一步以阵元位置为索引,计算阵因子及馈电相位。
%% 7*7单元天线合成
% 已知信息****************************************************************
mLine = 7;% y方向单元个数
nRow = 7;% x方向单元个数
dxmm = 12.5;% x方向单元间距,单位:mm
dymm = dxmm;% y方向单元间距,单位:mm
f0Ghz = 10;% 工作频点,单位:GHz
thetaScanDeg = 0;% 波束指向θ角
phiScanDeg = 0;% 波束指向φ角
% 单元方向图信息(以主极化分量为例)
Theta;%2D远场的theta角矩阵
Phi;%2D方向图的phi角
FieldThetaComplex;% 2D远场的复数值
% 已知信息****************************************************************
% 求解*********************************************************************
c0 = 3*1e8;
lamda0 = c0./(f0Ghz*1e9);
beta0 = 2*pi/lamda0;
% 生成天线位置坐标。
xPosmm = -dxmm*(nRow-1) /2:dxmm:dxmm*(nRow-1) /2;
yPosmm = -dymm*(mLine-1)/2:dymm:dymm*(mLine-1)/2;
[xMatrixPosmm yMatrixPosmm] = meshgrid(xPosmm,yPosmm);
% 波束扫描,相邻列(delPhiX)与相邻行(delPhiY)所需的单位相位差
delPhiXDegFed = rad2deg(beta0*(dxmm*1e-3)*sind(thetaScanDeg)*cosd(phiScanDeg));% 单位:°
delPhiYDegFed = rad2deg(beta0*(dymm*1e-3)*sind(thetaScanDeg)*sind(phiScanDeg));
% 方向图合成及波束扫描
FieldThetaSynthesisComplex = 0;
FieldPhiSynthesisComplex = 0;
delPhiXY = 0;%第1个单元初始相位
for iLine = 1:mLine%先固定行
for iRow = 1:nRow% 不同的列
delPhiXArrayRad = (dxmm*1e-3).*sind(Theta).*cosd(Phi)/lamda0*2*pi .*(iRow-1);% 单位:deg。相比于基准阵元,子阵元在x方向积累的相位
delPhiYArrayRad = (dymm*1e-3).*sind(Theta).*sind(Phi)/lamda0*2*pi.*(iLine-1);% 单位:deg。相比于基准阵元,子阵元在y方向积累的相位
delPhiArrayRad = delPhiXArrayRad+delPhiYArrayRad;% 相比于基准阵元,子阵元阵积累的总相位
delPhiXY(iLine,iRow) = delPhiXDegFed*(iRow-1)+delPhiYDegFed*(iLine-1);% 单位:deg。波束扫描,计算每个位置的单元天线所需馈的相位量
FieldThetaSynthesisComplex = FieldThetaSynthesisComplex + FieldThetaComplex.*exp( 1j.*delPhiArrayRad )*exp(-1j.*deg2rad(delPhiXY(iLine,iRow)));% 单元方向图,先乘阵因子,再加馈电的相位
FieldPhiSynthesisComplex = FieldPhiSynthesisComplex + FieldPhiComplex .*exp( 1j.*delPhiArrayRad )*exp(-1j.*deg2rad(delPhiXY(iLine,iRow)));
end
end% 方向图合成及波束扫描完毕四、结果对比
4.1 1D结果对比
波束扫描角度(0,0),截取phi=0°的平面上的方向图,归一化对比结果如下:
(0,0)-phi=0
波束扫描角度(60,30),截取phi=30°的平面上的方向图,归一化对比结果如下:
(60,30)-phi=30
4.2 2D结果
调用Matlab的sph2cart函数,画出3D方向图如下。
波束扫描角度:(0,0)
![]()
代码计算-3D-(0,0)
波束扫描角度:(60,30)
代码计算-3D-(60,30)