超简单理解L0、L1、L2范数原理及作用
L0,L1,L2范数在机器学习中的应用个人理解
博文针对L0、L1、L2范数原理及在机器学习中作用进行了非常通俗易懂的解释,为博主了解相关概念后自我理解,相信对于看完本篇分析的读者来说对理解这几个范数作用将有较大帮助,阅读前,推荐可以先阅读(L1范数与L2范数区别)这个博主写的更系统介绍,再看我这篇;对范数在机器学习中应用有所了解的可以直接看我这篇。
1、把结论放在前面
对于L0、L1、L2范数定义和在机器学习中的作用,相信大家都已经了解,具体就是:
(1)L0范数是指向量中非0的元素的个数。其作用可以提高模型参数的稀疏性,但是L0范数很难优化求解。
(2)L1范数是指向量中各个元素绝对值之和。其作用也是可以提高模型参数的稀疏性,效果没有L0范数好,但是更容易求解,更常用。
(3)L2范数是指向量各元素的平方和然后求平方根。其作用是减小模型所有参数大小,可以防止模型过拟合,也很常用。
2、前言
首先,来理解下稀疏性这个概念,简单直观解释就是对于一组数据(假设为x1,x2,x3,…,x1000),其中只有部分,比如(x100,x200…,x1000)这十组数据大小较大比如为1,其它都为0或者接近0,这就代表这组数据具有稀疏性。那么为什么要考虑数据的稀疏性呢?这个可能很多人也会想到“压缩感知”,但是我引用一个直观例子:假如判断一个患者是否患有某种疾病有100项判断指标,但是其中5项指标非常重要,假如让医生对100个指标每个都考虑,那将无疑是个大的工作量,而且对于其他95项指标很多工作都是没起什么作用的,所以这里就需要只考虑那5项指标即可,这就是数据稀疏性处理,就可以用到这几个范数,下面我将主要从稀疏性这一个方面来详细讲解我对于L0,L1,L2范数理解。
3、分析
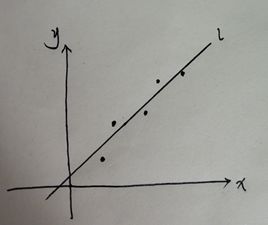
考虑一个一阶线性回归问题:
对于这类问题,我们是希望找到一个y=wx+b的方程去拟合这些点,方法也很简单,通过最小二乘法也就是:min{∑(yi实-yi)2}也就是min{∑(yi实-(wxi+b))2},对于这个简单问题,可以得到一个确定的解w0和b0,而这是对于一个参数w来说,这时,假如设定其方程为y=w1x+w2x+b,也就是w的参数为w1和w2,不用说,这里就会有w0=w1+w2,记住这个等式,很重要!
这个时候,假如我要求w1和w2满足稀疏性怎么办?也就是最好一个为0,另一个为w0。Ok,下面我们继续来考虑用最小二乘法方程来得出w1和w2值:min{∑(yi实-(w1xi+w2xi+b))2},其实,这个结果也还是会满足w1+w2=w0,具体w1和w2等于多少,不能确定,无法保证稀疏性。
3.1 L0范数:
这个时候假如加入约束条件:min{∑(yi实-(w1xi+w2xi+b))2+λ||w||0},这里||w||0是w的L0范数,λ是约束项系数,也就是求解min{∑(yi实-(w1xi+w2xi+b))2+λ(“w1和w2中非0的个数”)}这个时候,假如要保证其最小,就需要上面两项式子都相对最小,对于第二项式子,最好结果就是满足其中一个w参数为0,也就是w1或者w2为0,另一个参数等于w0(实际按上面公式是略小于w0,这里及后面假设等于w0,不影响分析)。所以L0范数实现了参数稀疏性。
3.2 L1范数
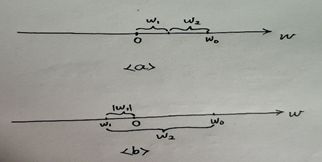
同理,使用L1范数后最小二乘法公式为:min{∑(yi实-(w1xi+w2xi+b))2+λ(|w1|+|w2|)},这里来看一张图片理解:
对于情况a,也就是w1和w2都为正,这个时候上面公式变为:min{∑(yi实-(w1xi+w2xi+b))2+λ(w1+w2)},由于w0=w1+w2,所以也就是min{∑(yi实-(w1xi+w2xi+b))2+λw0},其中w0为定值,所以这里不起到参数稀疏作用,但是对于情况b来说,也就是一个为正一个为负,这样使得(|w1|+|w2|)这项变大,而为了让其最小,其结果就是w1为0,w2=w0,所以也起到稀疏化作用。
3.3L2范数
同理,引入L2范数后,得到最小二乘法公式为:min{∑(yi实-(w1xi+w2xi+b))2+λ(w12+w22)1/2},将公式转换后变为:min{∑(yi实-(w1xi+w2xi+b))2+λ((w1+w2)2-2w1w2)1/2},将w0=w1+w2带入,等于:min{∑(yi实-(w1xi+w2xi+b))2+λ(w02-2w1w2)1/2},为了让第二项也就是:λ(w02-2w1w2)1/2最小,需要满足w02-2w1w2最小,也就是-w1w2最小,令w2=w0-w1,得到-w1w2=w12-w1w0下面参考下图理解:
可以看到当w1等于w0/2时满足其最小,也就是说L2范数更大作用是将w0这个参数值平均分给w1,w2,使其参数都变小,当w的个数很多时,相当于其它博主说的都趋于0,但是不等于0。
分析到这里了,我们来继续看看L3范数有什么性质,为什么只看到过分析L0、1、2范数,却不见L3范数,继续使用上面方法,最小化公式为:min{∑(yi实-(w1xi+w2xi+b))2+λ(w13+w23)1/3},变形为:min{∑(yi实-(w1xi+w2xi+b))2+λ((w1+w2)3-3w1w2(w1+w2))1/3},对于第二项:((w0)3-3w1w2(w0))1/3我们可以继续变形为求:-3w1w2(w0)最小值,也就是求-w1w2最小值,这就又回到了L2范数问题了。
4、总结
经过上面推导理解,可以看出,L0就是直接减少有效参数个数,对于L1在这里是只对于符号不一样参数可以使其中一部分参数变为0,L0和L1范数都可以使模型参数稀疏化;对于L2不能使参数为0,但可以使其总体都变小。