自监督学习——旋转篇
自监督学习——旋转篇
随着MoCo, SimCLR, BYOL等工作的提出将基于
对比学习框架的自监督学习推到了一个新的风口,博主也写了一篇MoCo v1原理解析,如果大家想了解基于对比学习的自监督学习基本原理可以参考一下这篇博客。不过这不是本篇博客的重点,博主写这篇博客的主要目的是给大家介绍基于旋转的自监督学习。博主会通过两篇基于旋转的自监督学习论文的原理讲解让大家更好地了解到这种自监督学习的方式。
PS:自监督学习可以看成是无监督学习的一种形式,有关的讨论在MoCo的论文之中也有介绍,本篇博客在这里使用自监督学习这个词
文章目录
- 自监督学习——旋转篇
- 1. Unsupervised Representation Learning By Predicting Image Rotations
-
- 1.1 Thinkings
- 1.2 Methodology
- 2. Self-Supervised Representation Learning by Rotation Feature Decoupling
- 2.1 Thinkings
- 2.2 Methodology
-
- 2.2.1 Rotation feature decoupling
- 2.2.2 Image rotation prediction
- 2.2.3 Noisy rotated images
- 2.2.4 Feature decoupling
- 2.2.5 Image instance classification
1. Unsupervised Representation Learning By Predicting Image Rotations
ICLR2018
1.1 Thinkings
自监督学习提出的一个核心motivation就是如何去更好地利用那些大量,难以用人工完全去标注的数据,让训练后的模型迁移到downstream tasks(例如语义分割、物体检测,图像分类等等)之后能够媲美甚至超过经过监督学习后的模型迁移到downstream tasks之后的表现。
自监督学习顾明思意就是让网络模型自己去监督自己,而没有标签该去怎么监督网络模型呢?于是,聪明的人们就提出可以自己去定义一些pretext tasks,利用一些图像变换的方式去生成pseudo labels,用这些生成的伪标签去监督网络完成这些代理任务。
本篇论文的作者就提出了一个pretext task,即通过旋转将图像随机旋转为0, 90, 180和270°,然后让网络去学习并预测输入的图片到底旋转了多少度。作者觉得之所以可以这么做的原因就是,要想让网络知道图像到底旋转了多少度的前提就是网络已经可以理解图像中物体位置,类型和姿势等概念了。如果网络不能够理解这些概念的话,它就无法区分出来图像到底旋转了多少度。(rebuttal专用)

1.2 Methodology

整个基于旋转的自监督框架简单且有效,即将一张原始图像随机旋转0, 90, 180和270°,把这四种旋转类别划分为四个类,图像如果旋转0°那么它的y=0,旋转90°那么它的y=1,其他类似。pretext task就是让网络预测这个图像属于哪一类的旋转,即将网络预测旋转角度的问题转换为了一个十分简单的四分类问题。
这里有个小细节需要注意一下,就是作者发现一次性将图像旋转0, 90, 180和270°,即一次输入四种不同旋转角度的图像比随机将图像从四种中旋转一个角度的效果会更好。不过博主觉得这么做也有一些弊端,一次性将图像旋转这么多角度就会将batch size扩大4倍,这样就很吃计算资源,也就是如果你的计算设备最大一次能输入32张图像,这32张图像其实只来自于8张不同的图像。如果你想要输入32张不同图像那就会导致你的一个batch会有128张图像。
2. Self-Supervised Representation Learning by Rotation Feature Decoupling
CVPR2019
2.1 Thinkings
这篇论文就是基于上一篇的工作将旋转自监督做了进一步发展,从标题就可以看出来这篇论文和核心卖点就是Rotation Feature Decoupling,所以本论文就围绕着怎么将feature解耦为rotation unrelated feature和rotation related feature,并如何利用这两种特征进行自监督训练这两个方面展开论述。PS:网上对这篇论文的评价褒贬不一,在这里博主不予置评,只是和大家分享一下我的阅读心得。
2.2 Methodology
2.2.1 Rotation feature decoupling
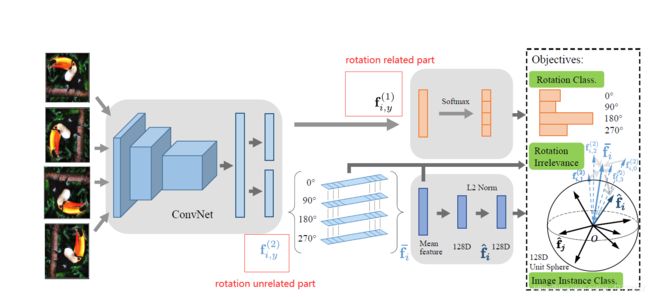
作者采用的decouple策略十分监督,即将ConvNet的特征经过编码得到的一维向量平分为rotation related part ( f i , y ( 1 ) f^{(1)}_{i,y} fi,y(1))和rotation unrelated part ( f i , y ( 2 ) f^{(2)}_{i,y} fi,y(2))两个部分。这里作者其实也没有解释为什么。虽然编码向量每一个维度就可以代表某一种特征,例如物体大小,是否有嘴巴,是否有旋转等等,也就意味着它肯定会包含rotation related part和rotation unrelated part这两个部分,但是并不一定前者就是编码向量的前半部分而后者就是编码向量的后半部分。
2.2.2 Image rotation prediction
这个部分就是上一篇论文的工作,也可以理解为这篇论文的基础。同样,本篇论文将图像旋转0,90,180和270°,把图像旋转的预测问题转换为一个四分类的问题。其objective function如下:
m i n θ 1 N K ∑ i = 1 N ∑ y = 1 K l ( F ( X i , y ; θ ) , y ) \mathop{min} \limits_\theta \frac{1}{NK} \sum^N_{i=1}\sum^K_{y=1}{l(F(X_{i,y};\theta), y)} θminNK1i=1∑Ny=1∑Kl(F(Xi,y;θ),y)
其中K=4,即四种旋转角度, θ \theta θ代表网络参数, X i , y X_{i,y} Xi,y代表第i个图像旋转了 ( y − 1 ) × 90 ° (y-1)\times90° (y−1)×90°, l ( ⋅ ) l(\cdot) l(⋅)代表交叉熵损失。
2.2.3 Noisy rotated images
这里的处理比较有意思,作者借鉴了PU learning的思想,即估计的条件概率与样本的噪声率有关,作者就做了一个权重机制,希望通过权重去控制噪声样本对于loss的贡献(rotation agnostic images其实也算是一种带有噪声的样本,并且由于其原方向不明确,所以刚好也符合PU learning中未标记样本的标准)。
首先利用一个二分类判断样本是否旋转了,再根据旋转概率判断权重:
w i , y = { 1 y=1 1 − F ~ ( X i , y ) γ y!=1 w_{i,y}= \begin{cases} 1& \text{y=1}\\ 1-\tilde{F}(X_{i,y})^\gamma& \text{y!=1} \end{cases} wi,y={11−F~(Xi,y)γy=1y!=1
其中 F ~ ( X i , y ) \tilde{F}(X_{i,y}) F~(Xi,y)就是二分类输出图像是否旋转的概率, γ \gamma γ作为一个参数控制概率的权重。
然后把上面的那个权重整合到Image rotation prediction中得到:
m i n θ 1 N K ∑ i = 1 N ∑ y = 1 K w i , y l ( F ( X i , y ; θ ) , y ) \mathop{min} \limits_\theta \frac{1}{NK} \sum^N_{i=1}\sum^K_{y=1}{w_{i,y}l(F(X_{i,y};\theta), y)} θminNK1i=1∑Ny=1∑Kwi,yl(F(Xi,y;θ),y)
2.2.4 Feature decoupling
作者在这里采用了一个最简单的分割方式,即将representation vector平分为rotation related part和rotation unrelated part, f = [ f ( 1 ) T , f ( 2 ) T ] T f = [f^{(1)T}, f^{(2)T}]^T f=[f(1)T,f(2)T]T,所以有关rotation related part的损失就是:
m i n θ 1 N K ∑ i = 1 N ∑ y = 1 K w i , y l ( F ( f i , y ( 1 ) ; θ ) , y ) \mathop{min} \limits_\theta \frac{1}{NK} \sum^N_{i=1}\sum^K_{y=1}{w_{i,y}l(F(f^{(1)}_{i,y};\theta), y)} θminNK1i=1∑Ny=1∑Kwi,yl(F(fi,y(1);θ),y)
rotation unrelated part这个部分作者则是想让各个旋转角度都可以靠近均值,即:
m i n θ 1 N K ∑ i = 1 N ∑ y = 1 K d ( f i , y ( 2 ) , f i ˉ ) \mathop{min} \limits_\theta \frac{1}{NK} \sum^N_{i=1}\sum^K_{y=1}{d(f^{(2)}_{i,y},\bar{f_i})} θminNK1i=1∑Ny=1∑Kd(fi,y(2),fiˉ)
其中 f i ˉ \bar{f_i} fiˉ就是四个旋转角度representation vector的均值, d ( ⋅ ) d(\cdot) d(⋅)代表欧式距离。
2.2.5 Image instance classification
作者加入了有关image instance classification的损失,不过这个部分就和MoCo那些大差不差,这里不做深入讨论。