【论文笔记】基于分层深度强化学习的移动机器人导航方法
目录
- 摘要
-
- 关键词
- 0 引言
- 1 基于分层深度强化学习的导航方法
-
- 1.1 模型框架
-
- 1.1.1 避障控制模型
- 1.1.2 目标驱动控制模型
- 1.1.3 行为选择模型
- 1.2 模型训练
- 2 实验分析
-
- 2.1 实验设置
- 2.2 实验结果与分析
-
- 2.2.1 训练与测试实验结果
- 2.2.2 可视化导航效果
- 2.2.3 真实环境下的导航实验
- 3 结论
摘要
- 针对:基于深度强化学习 (deep reinforcement learning, DRL) 的分层导航方法在包含长廊、死角等结构的复杂环境下导航效果不佳的问题
- 提出:基于 option-based 分层深度强化学习 (hierarchical deep
reinforcement learning, HDRL) 的移动机器人导航方法
具体内容:
- 低层的避障和目标驱动控制模型分别实现避障和目标接近两种行为策略;
- 高层的行为选择模型可自动学习稳定、可靠的行为选择策略;
- 通过训练,学习到的避障策略更加适用于复杂环境下的导航任务;
关键词
- 深度强化学习;
- 分层深度强化学习;
- 移动机器人;
- 导航;
- 避障;
- 策略学习
0 引言
传统的移动机器人导航方法:
- 需要高精度传感器构建环境地图;
- 依赖专家经验人为设计规则;
- 不足之处——在复杂环境较难导航;
现有 DRL 导航方法的研究:
- 将导航任务视为避障与目标接近两个子任务的结合;
- 分别设计奖励函数, 引导移动机器人在避开障碍的同时接近目标点,但是设计奖励函数需要较多的先验知识;
- 在长廊、死角处容易出现局部最小;
基于 DRL 的分层导航方法:
| 学者 | 工作 | 效果 | 引用 |
|---|---|---|---|
| Zhang 等 | 基于动作优势加权的策略融合方法 | 避障和目标接近两种低层行为策略均通过独立训练 DRL 获得,通过人为设计的规则对低层策略的动作优势值进行加权, 得到用于导航的控制动作. | Zhang W, Zhang Y, Liu N. Danger-aware adaptive composition of DRL agents for self-navigation[J]. Unmanned Systems, 2020, 9(1): 1-9. |
| Ding 等 | 用于多机器人导航任务的分层控制方法 | 利用 DRL 和简单规则分别得到避障策略和目标接近策略, 并对相应的控制动作进行加权输出;能够降低策略学习的难度,但是其高层策略始终依赖人为设计的调控规则。 | Ding W, Li S, Qian H, et al. Hierarchical reinforcement learning framework towards multi-agent navigation[C]. In: Proceedings of the IEEE International Conference on Robotics and Biomimetics. Kuala Lumpur: IEEE, 2018: 237-242. |
分层深度强化学习:
| 类型 | subgoal-based | option-based |
|---|---|---|
| 特点 | 高层策略负责生成子目标, 再由低层策略输出控制动作进行实现 | 高层策略负责在多个低层策略中进行选择, 再由被选择的低层策略输出控制动作 |
| 例子 | 用于实现移动机械臂复杂控制的 HDRL 方法 | 实现六足机器人移动控制 |
| 主要内容 | 高层策略用于输出移动底盘或机械臂的子目标姿态, 而低层策略负责控制移动机械臂到达相应的子目标姿态, 使其实现移动或开门操作 | 低层策略负责控制机器人关节完成前进、转向等基础运动;高层策略负责规划低层策略的执行顺序, 从而引导机器人到达目标位置. |
| 期刊引用 | Li C, Xia F, Martín-Martín R, et al. Hrl4in: hierarchical reinforcement learning for interactive navigation with mobile manipulators[C]. In: Proceedings of the Conference on Robot Learning. Virtual Event: PMLR, 2020: 603-616. | Li T, Lambert N, Calandra R, et al. Learning generalizable locomotion skills with hierarchical reinforcement learning[C]. In: Proceedings of the IEEE International Conference on Robotics and Automation. Paris: IEEE, 2020: 413-419. |
| 缺点 | 依赖先验知识设计具有任务特异性的子目标空间 | 仅考虑在无障碍物的简单环境中对机器人进行移动控制 |
本文主要工作叙述:
- 采用基于 option-based HDRL 的模型框架
- 通过设计基于规则的目标驱动控制模型和基于 DRL 的避障控制模型, 分别实现目标接近与避障两种低层行为策略
- 利用基于 DRL 的行为选择模型学习稳定、可靠的高层行为选择策略, 有
效避免了对人为设计调控规则的依赖 - 在训练避障控制模型的同时训练行为选择模型, 并将接近行为的经验数据也存入避障控制模型的经验池
1 基于分层深度强化学习的导航方法

高层的行为选择模型采用全连接神经网络;
低层的避障控制模型也采用类似的全连接神经网络, 负责学习避障策略;
低层的目标驱动控制模型则采用基于规则的控制器, 负责实现目标接近策略.
1.1 模型框架
1.1.1 避障控制模型
采用竞争双深度 Q 网络 (dueling double deep Q-network,D3QN)实现避障控制模型
刘建伟, 高峰, 罗雄麟. 基于值函数和策略梯度的深度强化学习综述 [J]. 计算机学报, 2019, 42(6): 1406-1438.
- 状态:连续三帧的 2D 激光雷达扫描数据。
每一帧数据为长度为 40 的一维数组;
每个数组元素对应于单束激光的距离测量值;
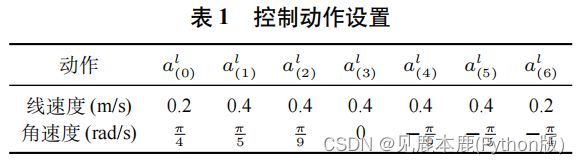
按采集时间顺序进行拼接, 构成输入状态 s t l [ 23 ] s_{t}^{l[ 23 ]} stl[23] - 动作:7 种离散动作 a l ( 0 ) , . . . , a l ( 6 ) a_{l}(0), . . . , a_{l}(6) al(0),...,al(6)。
每一种动作 a l ( i ) a_{l}(i) al(i) 都对应于一对预设的线速度和角速度 ( v i , ω i ) (v_{i}, ω_{i}) (vi,ωi). - 网络结构:全连接层对输入状态编码;输入两条支路分别得到状态价值 (state-value) V ( s t l ) V (s^{l}_{t}) V(stl) 和动作优势值 (action-advantage) A ( s t l , a t l ) A (s^{l}_{t}, a^{l}_{t}) A(stl,atl);两值相加得到每一种动作的动作价值 (action-value) Q ( s t l , a t l ) Q (s^{l}_{t}, a^{l}_{t}) Q(stl,atl);
状态价值:表征当前状态能够带来的长期收益;
动作优势值:用于衡量不同动作之间的相对优劣;
动作价值:用于表征当前动作能够带来的长期收益, 其中动作价值最大的动作将作为避障控制模型的输出
更新公式如下:
Q ( s t , a t ; θ ) = Q ( s t , a t ; θ ) + α ( y t − Q ( s t , a t ; θ ) ) y t = r t + γ Q ^ ( s t + 1 , arg max a ∈ A l Q ( s t + 1 , a ; θ ) ; θ − ) Q(s_{t},a_{t};\theta) = Q(s_{t},a_{t};\theta) + \alpha(y_{t} - Q(s_{t},a_{t};\theta)) \\ y_{t} = r_{t}+\gamma \hat{Q} (s_{t+1}, \argmax_{a \in A_{l}} Q (s_{t+1}, a; \theta) ; \theta^{-}) Q(st,at;θ)=Q(st,at;θ)+α(yt−Q(st,at;θ))yt=rt+γQ^(st+1,a∈AlargmaxQ(st+1,a;θ);θ−)
奖励函数设置如下:
r t l = v t + ( r c ) t ( r c ) t = { r c o l l i s i o n D t < R r o b o t − λ c D t D t ≥ R r o b o t r_{t}^{l} = v_{t}+(r^{c})_{t} \\ (r^{c})_{t} = \begin{cases} r_{collision} &D_{t}
D t → D_{t} \rightarrow Dt→ 移动机器人当前时刻与障碍之间的最小距离;
R r o b o t → R_{robot} \rightarrow Rrobot→ 移动机器人底盘半径;
r c o l l i s i o n → r_{collision} \rightarrow rcollision→ 预定义参数;
1.1.2 目标驱动控制模型
- 控制器首先获取目标点的实时坐标 [ x t , y t ] [x_{t}, y_{t}] [xt,yt]
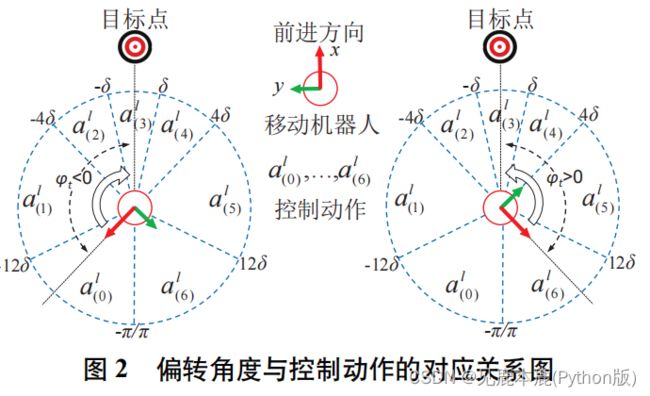
- 计算移动机器人前进方向与目标方向之间的偏转角度 ϕ t \phi_{t} ϕt
ϕ t = { a r c t a n ( y t x t ) x t > 0 a r c t a n ( y t x t ) + ( y t ∣ y t ∣ ) π x t < 0 \phi_{t} = \begin{cases} \mathbf{arctan}(\frac{y_{t}}{x_{t}}) &x_{t} \gt 0 \\ \mathbf{arctan}(\frac{y_{t}}{x_{t}})+(\frac{y_{t}}{|y_{t}|})\pi & x_{t} \lt 0 \end{cases} ϕt={arctan(xtyt)arctan(xtyt)+(∣yt∣yt)πxt>0xt<0 - 根据图片将偏转角度 ϕ t \phi_{t} ϕt 映射到相应的动作。在某个范围内选择某套参数进行运动。
1.1.3 行为选择模型
| 项目 | 内容 |
|---|---|
| 状态 | 激光雷达扫描数据外 + 目标点的相对坐标 + 移动机器人的线速度与角速度 |
| 动作 | 2 种离散动作,分别对应于避障和目标接近两种行为,动作价值较大的动作用于激活相应的行为策略 |
| 模型 | D3QN |
行为选择模型的决策间隔在选择目标接近行为时设为 1 个时间步 (time step), 而在选择避障行为时设为 n n n( n n n >1) 个时间步, 从而有利于缩短决策链长度, 降低策略学习的难度。
y t = ∑ τ = 0 k − 1 γ τ r t + τ h + γ k Q ^ ( s t + k h , arg max a ∈ A h Q ( s t + k h , a ; θ ) ; θ − ) y_{t} = \sum\limits_{\tau=0}^{k-1}\gamma^{\tau}r_{t+\tau}^{h}+\gamma^{k}\hat{Q}(s_{t+k}^{h},\argmax_{a \in A_{h}}Q(s_{t+k}^{h},a;\theta);\theta^{-}) yt=τ=0∑k−1γτrt+τh+γkQ^(st+kh,a∈AhargmaxQ(st+kh,a;θ);θ−)
s t + k h s^{h}_{t+k} st+kh 和 a t + k h → a^{h}_{t+k} \rightarrow at+kh→ 下一次决策时的输入状态和输出动作;
r t + T h → r^{h}_{t+T} \rightarrow rt+Th→为时刻 t + T t + T t+T的即时奖励;
奖励函数设置如下:
r t h = ( r d ) t + ( r o ) t + ( r s ) t ( r d ) t = λ t ( d t − 1 − d t ) ( r o ) t = { λ o ( D t − D o ) , D t ≤ D t h r e s r o b s t a c l e , D t > D t h r e s ( r s ) t = { 20 , 到达目标点; − 20 , 发生碰撞则受到惩罚; r^{h}_{t} = (r^{d})_{t}+ (r^{o})_{t} + (r^{s})_{t} \\ (r^{d})_{t} = \lambda^{t}(d_{t-1}-d_{t}) \\ (r^{o})_{t} = \begin{cases} \lambda^{o}(D_{t}-D^{o}),&D_{t} \le D_{thres} \\ r_{obstacle},&D_{t} \gt D_{thres} \end{cases} \\ (r^{s})_{t} = \begin{cases} 20,到达目标点;\\ -20,发生碰撞则受到惩罚; \end{cases} rth=(rd)t+(ro)t+(rs)t(rd)t=λt(dt−1−dt)(ro)t={λo(Dt−Do),robstacle,Dt≤DthresDt>Dthres(rs)t={20,到达目标点;−20,发生碰撞则受到惩罚;
1.2 模型训练
传统避障方法:
- 首先使移动机器人与环境交互;
- 产生避障行为经验数据并存入避障控制模型经验池;
- 仅利用避障行为经验数据更新避障策略;
通过该训练方法学习到的避障策略虽然能够使机器人成功躲避障碍, 但易出现局部极小问题
算法1~参数更新:
- 机器人按照算法 2 执行一次动作;
- 利用 E 1 E_{1} E1 中的历史数据, 更新避障控制模型, 利用 E 2 E_{2} E2中的历史数据, 更新行为选择模型;
- 迭代 step1 到 step2, 总共 T 1 T_{1} T1 次;
- 机器人按照算法 2 执行一次动作;
- 利用 E 2 E_{2} E2中历史数据, 更新行为选择模型;
- 迭代 step4 到 step5, 总共 T 2 − T 1 T_{2} − T_{1} T2−T1 次;
算法2~环境交互
- 根据行为选择模型的输出选择行为;
- 如果选择目标接近行为, 根据目标驱动控制模型的输出执行 1 次动作, 产生的目标接近经验数据存入 E 1 E_{1} E1. 反之则根据避障控制模型的输出执行 n n n 次动作, 产生的避障经验数据存入 E 1 E_{1} E1;
- 产生的行为选择经验数据存入 E 2 E_{2} E2;
- 迭代 step1 到 step3, 直到回合终止;
2 实验分析
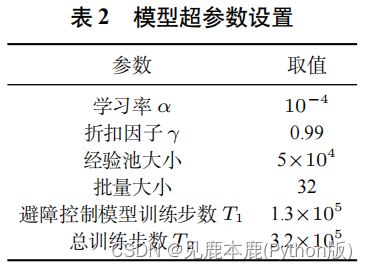
2.1 实验设置
2.2 实验结果与分析
2.2.1 训练与测试实验结果
对比模型:
| 模型 | 内容 |
|---|---|
| D3QN 方法 | 使用 D3QN 直接学习导航策略 |
| DAAC(danger-aware adaptive composition) 方法 | 基于动作优势加权的分层导航方法 |
| HDRL 方法 | 本文提出的 option-based HDRL 模型框架, 但在训练过程中不利用接近行为的经验数据对避障策略进行优化. |
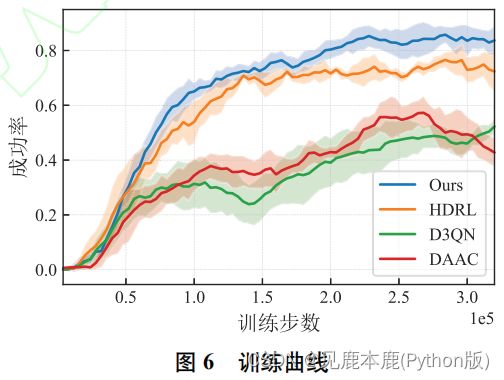
- D3QN 方法和 DAAC 方法的训练曲线增长缓慢, 表明移动机器人在复杂环境下学习导航策略的难度较大.
- HDRL 方法和本文方法的训练曲线在整个训练阶段稳定增长.
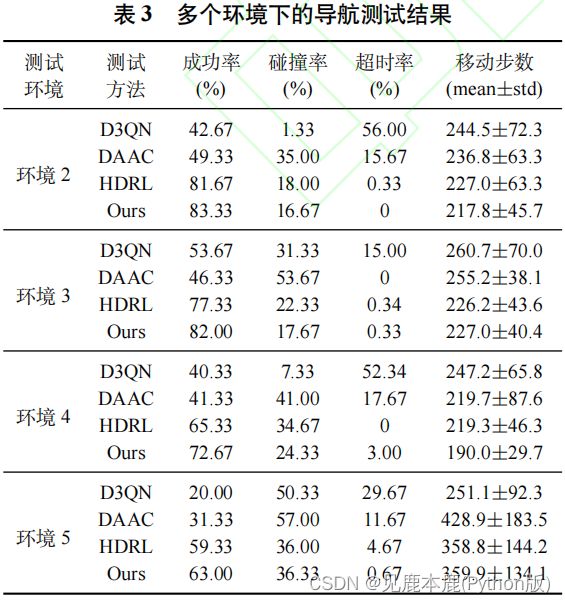
- 碰撞率表示发生碰撞回合数占总测试回合数的比例;
- 超时率表示超时回合数占总测试回合数的比例;
- 步数表示在成功回合中机器人移动的步数;
- D3QN 方法在测试环境 2-4 中的超时率显著高于其它方法, 表明非分层导航方法在复杂环境下容易产生局部极小问题.
- DAAC 方法依赖人为设计的调控规则难以得到较优的导航策略, 因此在测试环境 2-4 中的碰撞率显著高于其它方法.
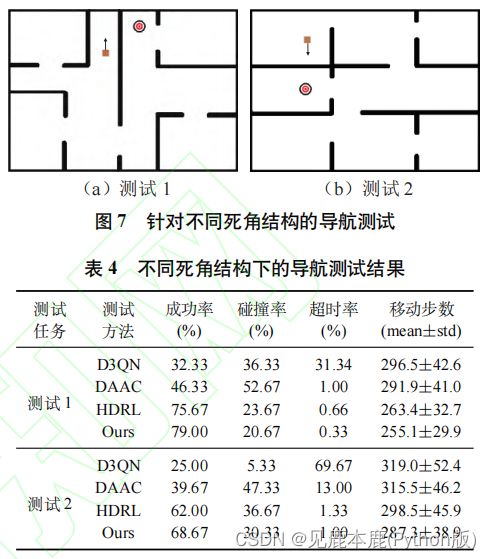
本文方法在两种死角结构中均取得了最高的导航成功率。
2.2.2 可视化导航效果

D3QN 方法进行导航时出现局部极小问题,导致移动机器人无法走出凹形区域;