MATLAB 传递函数的相关函数
1. 连续时间传递函数
1.1 多项式形式传递函数
num = 1; % 分子多项式的系数
den = [2, 3]; % 分母多项式的系数
G = tf(num, den) % 求传递函数1.2 因式乘积形式(零极点)传递函数
z = [1]; % 零点
p = [2,3]; % 极点
k = -4; % 增益
G = zpk(z, p, k) % 求传递函数1.3 由状态空间描述得到传递函数(单输入单输出)
A = [0 1; -1 -1]; % 系统矩阵
B = [0; 1]; % 输入矩阵
C = [1 0]; % 输出矩阵
D = 0; % 直接传递矩阵
[num, den] = ss2tf(A, B, C, D); % 求分子多项式与分母多项式
G = tf(num, den) % 求传递函数 2. 离散传递函数
如果想要从某个连续传递函数得到在特定采样周期下的离散函数,请看第3节。
离散时间传递函数的建立与连续时间基本一致,只需要引入一个采样周期![]() 。
。
请注意z变换与拉氏变换之间的区别,二者基本无共同点。
2.1 多项式形式离散传递函数
num = 1; % 分子多项式的系数
den = [2, 3]; % 分母多项式的系数
T = 1; % 采样周期(1s)
G = tf(num, den, T) % 求传递函数在matlab中,运行上述代码,可以得到传递函数![]() ,采样时间为1s。
,采样时间为1s。
2.2 零极点形式离散传递函数
z = [1]; % 零点
p = [2,3]; % 极点
k = -4; % 增益
T = 1; % 采样周期(1s)
G = zpk(z, p, k, T) % 求传递函数在matlab中,运行上述代码,可以得到传递函数![]() ,采样时间为1s。
,采样时间为1s。
3. 传递函数的化简与转化
3.1 连续传递函数与离散传递函数间的转化
3.1.1 连续传递函数到离散传递函数
(其余形式的连续传递函数同理,均是使用函数c2d)
num = 1; % 分子多项式的系数
den = [1, 1]; % 分母多项式的系数
G = tf(num, den) % 连续传递函数
T = 1; % 采样周期(1s)
Gz= c2d(G, T) % 离散传递函数3.1.2 离散传递函数到连续时间函数
(其余形式的离散传递函数同理,均是使用函数d2c)
num = 0.6321; % 分子多项式的系数
den = [1, -0.3679]; % 分母多项式的系数
T = 1; % 采样周期(1s)
Gz = tf(num, den, T) % 离散传递函数
Gs = d2c(Gz) % 连续传递函数3.2 因式乘积形式(零极点形式)与多项式形式的互相转化
3.2.1 因式乘积形式(零极点形式) 转化到 多项式形式
z = [1]; % 零点
p = [2,3]; % 极点
k = -4; % 增益
[num, den] = zp2tf(z, p, k); % 因式乘积形式(零极点形式) 转化到 多项式形式
G = tf(num, den) % 多项式形式3.2.2 多项式形式 转化到 因式乘积形式(零极点形式)
num = [1,2]; % 分子多项式的系数
den = [1,4,3]; % 分母多项式的系数
[z, p, k] = tf2zp(num, den); % 多项式形式 转化到 因式乘积形式(零极点形式)
G = zpk(z, p, k) % 零极点形式3.3 传递函数的化简
num = [1, 0]; % 分子多项式的系数
den = [1, 1, 0]; % 分母多项式的系数
G1 = tf(num, den) % 带有可以对消项的传递函数
G2 = minreal(G1) % 化简之后3.4 多项式形式中首一形式与尾一形式的互相转化
3.4.1 将传递函数化简为首1形式
num = 1; % 分子多项式的系数
den = [10, 1]; % 分母多项式的系数
G1 = tf(num, den) % 传递函数
G2 = minreal(G1) % 化简为首一形式3.4.2 将传递函数化简为尾1形式
G = tf(1, [1, 10]); % 获取传递函数
num = cell2mat(G.Numerator); % 分子多项式的系数
den = cell2mat(G.Denominator); % 分母多项式的系数
num = num/den(end); % 除以分母最后一项
den = den/den(end); % 除以分母最后一项
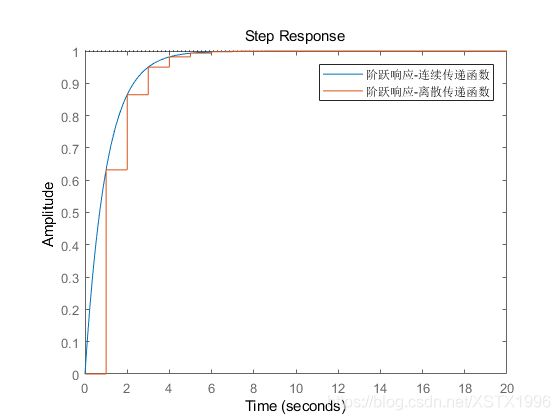
G2 = tf(num, den) % 化简为尾一形式3.5 求阶跃响应
Gs = tf(1, [1, 1]); % 连续时间传递函数
Gz = c2d(Gs, 1); % 获取对应的离散时间传递函数,采样时间T = 1s
step(Gs); % 连续传递函数的阶跃响应
hold on; % 保持图形
step(Gz); % 离散传递函数的阶跃响应
legend('阶跃响应-连续传递函数', '阶跃响应-离散传递函数'); % 添加图例