PyTorch-07 卷积神经网络（什么是卷积、卷积神经网络、池化层、Batch normalization、经典卷积网络、深度残差网络 ResNet、nn.Module、数据增强）

PyTorch-07 卷积神经网络（什么是卷积、卷积神经网络、池化层、Batch normalization、经典卷积网络(LeNet-5、AlexNet、VGG、GoogLeNet)、深度残差网络 ResNet、nn.Module（使用nn.Module的好处）、数据增强（Data Argumentation））

一、什么是卷积

deep learning 一般使用0-1这个范围，但是数据存储是0-255，所以我们加载进来时除以255这个分数，使其达到0-1这个区间内。

What’s wrong with Linear

全连接层，在pytorch中也叫线性层，线性层仅仅表达了全连接网络的线性部分，线性层后面会增加一个非线性单元，叫做激活函数，因此不论是叫线性层还是叫全连接层，都指的是整个网络。我们实现的时候linear是没有包含激活函数这部分的。

对于下图，这个神经网络一共有4层，3个隐藏层和1个输出层，input layer输入层是不把它计算在内的，仅仅作为数据的输入。对于某一层，是指这一层的权值w和这一层的输出加在一起叫做一层。

输入的本来是28*28的matrix，这里为了方便全连接层的处理，因此打平为784维的向量。中间节点全部去256，一共有4个hidden layer，每个hidden layer是256，和一个输出层10类。

这个网络一共有多少参数量呢？多少参数量就意味着有多少条线，784256 + 256256 + 256256 + 25610 = 390k parameter参数量。每一个参数是用一个四字节的浮点数来表示的。390k *4 = 1.6MB memory的显存

Receptive Field 感受领域（局部相关性）

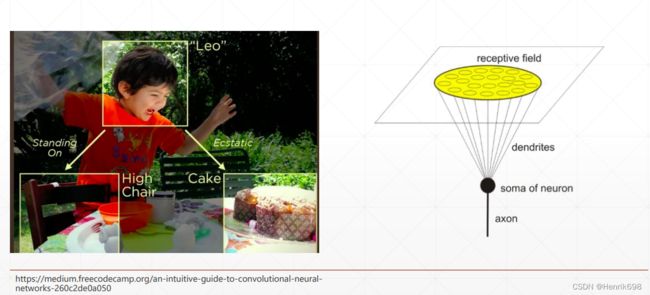
模仿人眼感受局部相关性的一个机制，提出了卷积神经网络，这里卷积指的就是局部相关性，一次感受的就是一个小方块，而不是一个大区间，一次感受的是一个小的视野，。

Weight sharing 权值共享

这样一个小窗口，会扫过一个大的图片，在扫合格大的图片过程中使用了同一个权值w，也就是w这个参数是不变的，扫完一次之后，只有在back propagate反向传播之后才更新一次w。因此小窗口扫描大图片的过程中，通过局部相关性促成这种共享的机制存在，使用相同的w扫描大图的过程叫做权值共享。以后会在RNN中使用权值共享这个概念在里面。使用权值共享会让参数量下降。

用于邮编的识别：LeNet-5，会让参数量下降了原来的1/6。

Convolution Operation卷积操作

卷积操作就是小窗口33不断的与大窗体对应位置进行计算，获得一个输出点，通过不断的循环，完成对所有点的计算后生成新的窗体，该新窗体大小和原来的窗体大小是相同的。

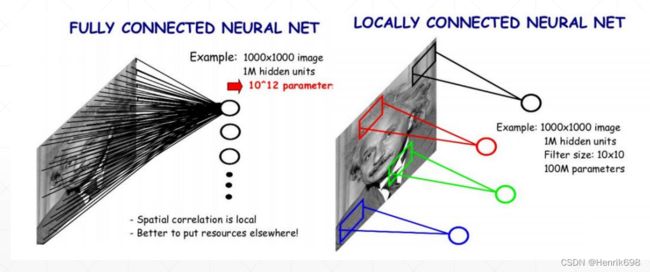
之前的连接是2828整个大窗体的连接，每个点都通过整个大窗体来进行计算，每个节点都有784条连线；而卷积计算只会和每个节点相关的9个节点相连线，这个小窗口只有9根线进行连接，其他的775条都是断开的。


小窗体和小窗体对应大窗体位置的小窗体可以进行矩阵的计算，也可以进行相应元素上的相乘后再累加，从而会的一个点，这种相乘在累加后生成一个点的操作叫做卷积操作。

Why call Convolution?为什么叫卷积?

卷积操作在信号处理邻域中：
是一个偏移的积分运算过程。





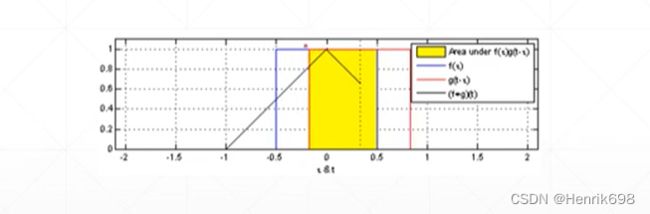
这种信号邻域的计算如何才能对应到图片中的卷积运算中呢？
图像上的积分运行，就是对应窗口位置相乘再累加。

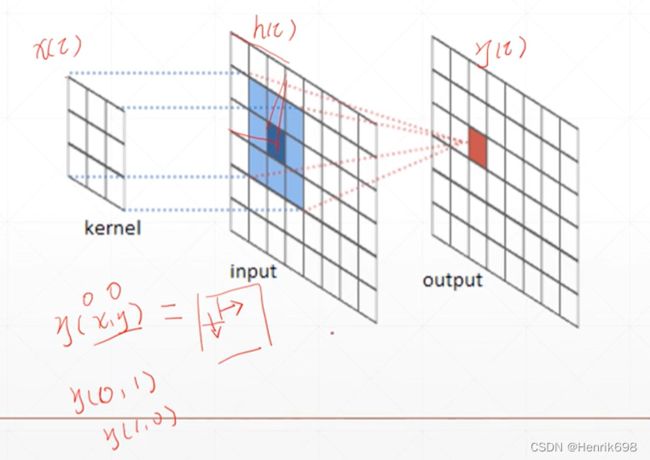
Convolution卷积

对一个图片进行Sharpen操作，让图片变得更锐化，因此我们就使用一个5*5的kernal核，和图片进行卷积运算。图像上的积分运行，就是对应窗口位置相乘再累加。

除了上面的Sharpen锐化操作，还有一个是Blur模糊化。

除了上面两个还有一个是Edge Detect边缘检测。

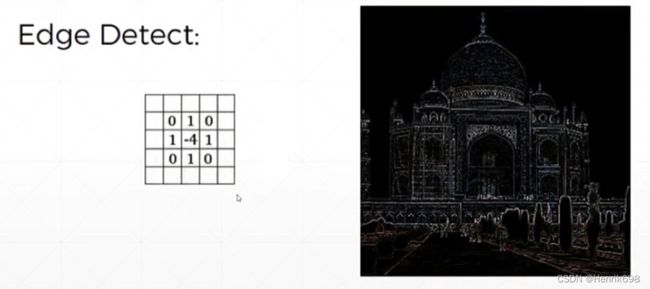
CNN on feature maps CNN专题图

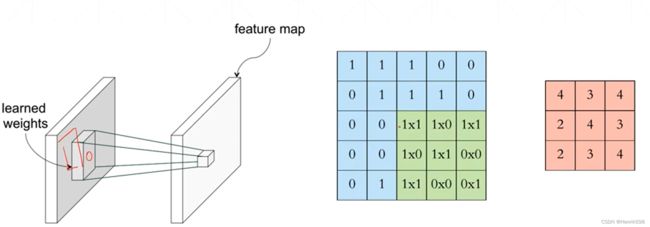
每次扫描使用的不同kernal，则获得的图片是不一样的，下面可以看到小窗体在开始是红色框，第二次是绿色框，这两次计算后生成的结果是不同，因为kernal不同。

二、卷积神经网络

计算结束后，原来的图片如果是2828，由于kernal是33，在靠近到原图片的边缘时，最边缘的一圈kernal是无法靠近的，因为如果将kernal中心点对准原图片边缘的像素，则kernal会有一些超出原图像，为了不让kernal不超出原图片，所以新图片是26*26，会比原来的小一圈。

如果进行padding填充操作，即让原来的2828周围增加一圈0，就可以保证输出的新函数是2828。

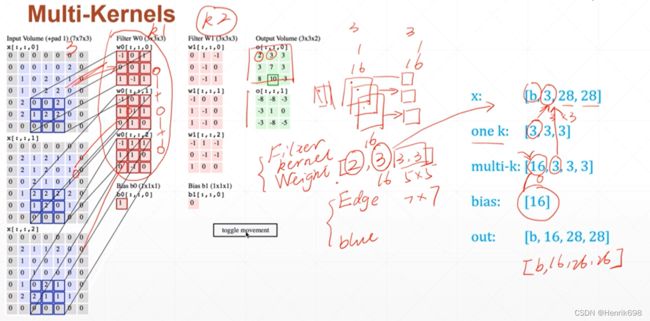
多个kernal代表着有多个不同的观察角度。
原图像(1,28,28)
kernal(7,3,3)
新图像(7,26,26)
卷积运算：

Notation注意

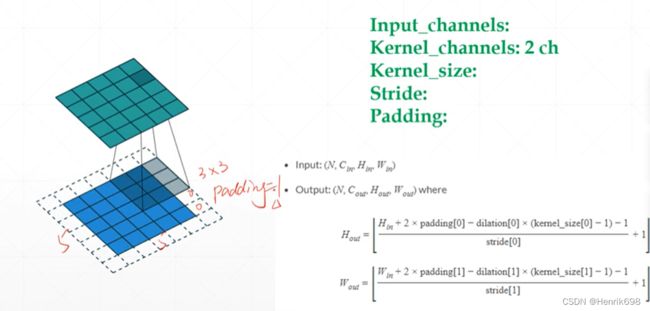
1、Input_channels：表示输入图片有几个通道，黑白图片通道数是1，彩色图片通道数3。
2、Kernal_channels：2 ch，这里是指kernal有一个Blur和一个Edge Detect组成的2 ch，(注意，如果输入图片是三通道的，则kernal就有三个与原图片对应，但是kernal的channel不是与原图片通道数来相互对应的，是与Blur和Edge Detect来对应的，所以kernal有2 ch，可以理解为kernal的类型数量，但是有3个一样的Blur和3个一样Edge与彩色图片相互对应，这里的3表示1个ch的与原彩色图片对应的三个通道)（这个很容易混淆，需要理解）。
3、Kernal_size：3*3
4、Stride：这里指的是移动的步长，kernal小窗体移动的步长。
5、Padding：这里指填充于原图片周围的一圈0，padding=1，表示一圈0，padding=2为二圈。

更加常见的情况 Multi-Kernels

LeNet-5 邮政编码的识别的网络：

Pyramid Architecture金字塔结构

representation learning 特征学习的由来：特征不断的提取的过程。

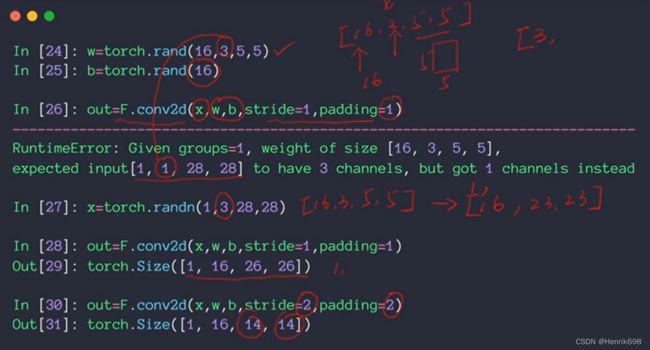
nn.Conv2d 类接口

stride=2，会有降维的效果，输出的新图会比原图小。
这里尽量不要直接使用layer.forward()。推荐使用实例的方法，out = layer(x)，这个其实是调用的是python的魔法 .call 函数。pytorch在__call__函数中封装了一些hooks，这些hooks有一些高阶的特性，如果要使用这些hooks，就必须要使用layer()类的实例来调用，如果使用layer.forward()这种方法，就没办法使用pytorch提供的一些hooks方法。不要直接调用.forward()。

Inner weight & bias

F.conv2d 函数式接口

三、池化层 (Pooling层,即下采样）Down/up sample

Outline
▪ upsample 上采样，和图片放大非常类似。
▪ Pooling 下采样，就意味着是将feature map变小的操作。
卷积神经网络配套的一个网络层叫：Pooling层
▪ ReLU

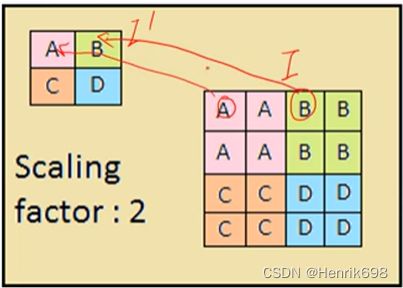
1、Downsample 下采样

对于图片数据而言，Downsample下采样类似于降维的这种操作。

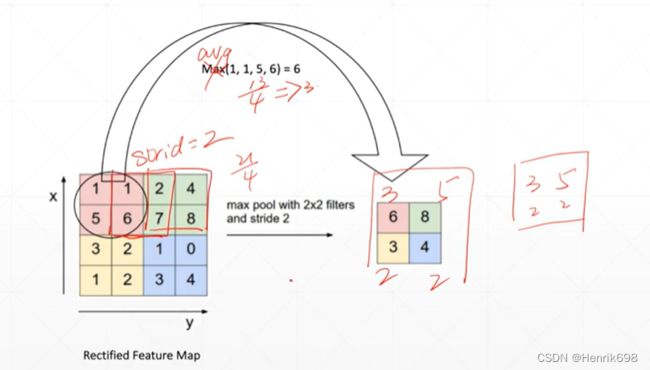
Max pooling

在卷积神经网络中，是使用max pooling来进行类似于上面那种降维操作的。

Avg pooling

就是获取小窗口所有像元的均值。

使用pytorch来完成pooling这样的操作

这里可以注意，convolution的kernal会改变原图像的channel，而这里的pooling是不会改变原图像channel的数量的。下面的代码可以看出输入和输出的channel是没有改变的，依然是16。

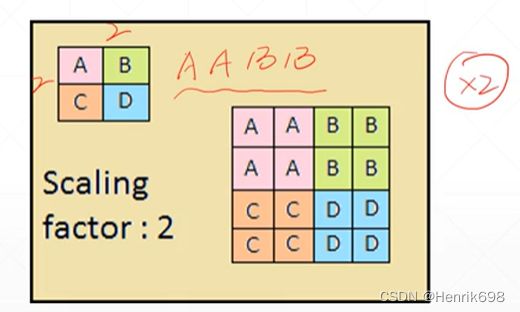
2、Upsample 上采样

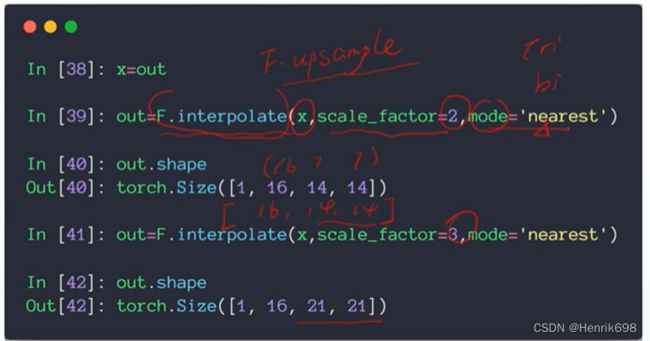
在pytorch中如何使用 F.interpolate

interpolate表示插值的意思。
这里依然是不会改变原图像的channel数量。下面的代码是pytorch自带的实现扩大方法，的对于tensor这种数据类型的可以直接使用的。

ReLU

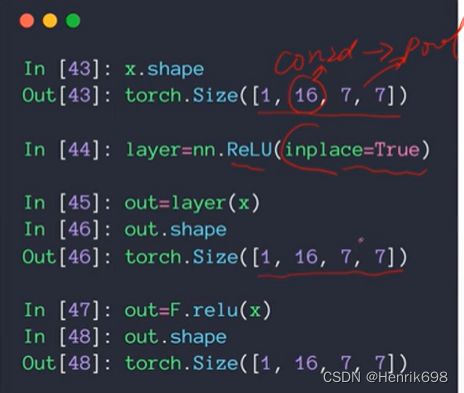
是将图片feature map中负的像元给去掉的过程，那些像元响应太低了，就把那些小于0的像元给去掉。下图中黑色部分就是响应太小了，去掉后就变成了右图的样子，像素值变为了0。

在pytorch中如何使用 F.relu()

inplace = True 表示可以使用原先变量的内存空间，这样可以减少内存的使用。可以发现使用relu后，输入和输出的shape是没有变化的，但是像元值发生了改变，最小值不在是负值，而变为了0。

四、Batch normalization（数据归一化方法）

重要概念，Batch normalization，这个概念会在卷积神经网络中、循环神经网络中等都会用到。
Batch Normalization是2015年一篇论文中提出的数据归一化方法，往往用在深度神经网络中激活层之前。. 其作用可以加快模型训练时的收敛速度，使得模型训练过程更加稳定，避免梯度爆炸或者梯度消失。. 并且起到一定的正则化作用，几乎代替了Dropout（dropout是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃）。

直观的解释Intuitive explanation

对于使用sigmoid函数来说，当输入大于某个区间范围后，sigmoid的导数会接近于0，这样就容易出现梯度离散的情况。因此很有必要对输入做一定的限制。normalization就是用来最这个限制的，让输入数据等效变换，使其输入的数据满足一定的正太分布N(0,σ^2)，希望这个值能够均匀落在0的附近，使其在小的范围内变动，这样再做下一层的时候，优化起来会更加方便。

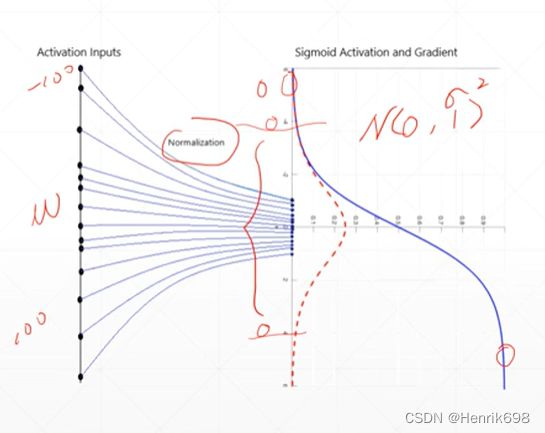
可以发现下图中，左侧的图，x1是在一个比较小的值，x2是在一个比较大的值，因此当w1进行改变时，x1的变化会比较小，当w2进行改变时，x2会急剧的变化，这样在搜索全局最小值的过程会比较曲折一些，左图的箭头所示。
如果x1和x2的范围是一样的，w1和w2对最终loss是一样的，会形成右图圆形的路径，在进行搜索的时候，不管从哪个点出发，梯度所指的方向都是全局最小解的方向。这样搜索过程会比较快捷方便稳定。

Feature scaling特征缩放

Batch Normalization

我们这里只看Batch normalization。

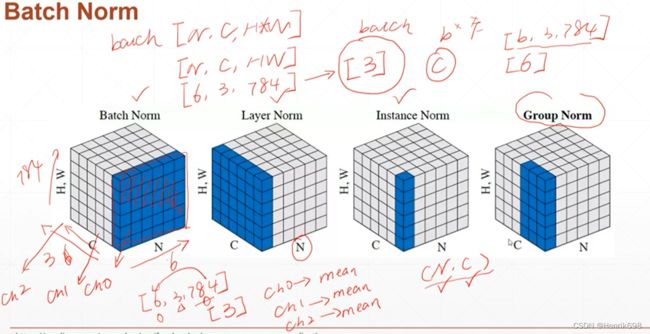
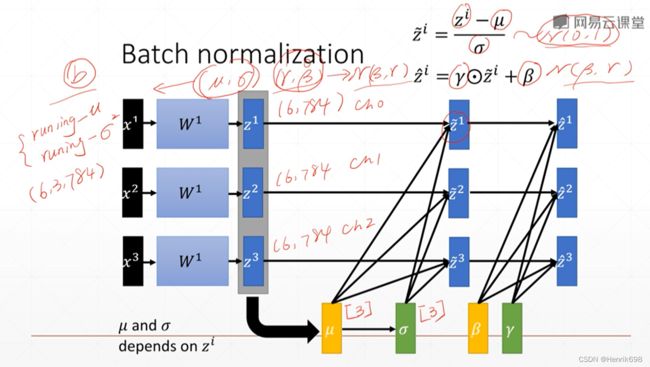
这里需要注意的是，μ和σ是统计出来的，是不需要参与反向传播（back propagation）的，是根据当前的batch里面的统计数据统计出来的；但是γ和β是学出来的，是需要梯度信息的，刚开始(γ=1, β=0)是没有影响，慢慢会学到一个N(β为均值, γ为方差)的偏置。
此外μ和σ会有一个历史记录，记录每一个batch的总的均值和总的方差，总的均值和总的方差在命名上μ和σ前面增加了一个running，running-μ和running-σ²，这样命名就是表示运行时候的统计数据，表示所有training出来的总的均值和总的方差。

利用pytorch进行这样的一个计算：这里是针对1维数据进行操作的。

import torch

from torch import nn

#这里是针对一个1维的feature，原来是(28,28)，只不过拉平了，变成了784。
x = torch.rand(100,16,784) #均匀分布在0到1之间
# print(x) #均匀分布的均值肯定是0.5


#这里的参数是给定的channel数量
#这里是有多少个channel，就统计出多少个数值
#这就意味着会生成16个统计信息，这些统计信息记录了每个channel的均值和方差。
layer = nn.BatchNorm1d(16)
print(layer)
#做一次forward运行后,会生成均值和方差，为当前x的。
#做完这个后，会自动更新一个全局的running-μ和running-σ²。
#对于只做一次运算的来收，μ和σ²就直接赋值为全局的了。
out = layer(x)

# print(out)
print(layer.running_mean)
print(layer.running_mean.shape)

print(layer.running_var)
print(layer.running_var.shape)

batch normalize规范化的写法

下面的步骤就是batch normalize train的过程。
1、第一步统计当前batch的μв均值和方差σ²в，这里还自动更新running-μ和running-σ²。
2、第二步进行normalize的操作。注意在进行normalize的时候分母会加一个很小的值10^-8，这样做是为了避免除零错误。计算完成后再进行一个平移β和缩放γ，使其达到N(均值β,方差γ)的正太分布。在反向传播（back propagation） 的时候，β和γ需要梯度信息，因此这两个参数会自动更新。

利用pytorch进行这样的一个计算：这里是针对2维数据进行操作的。

import torch
from torch import nn

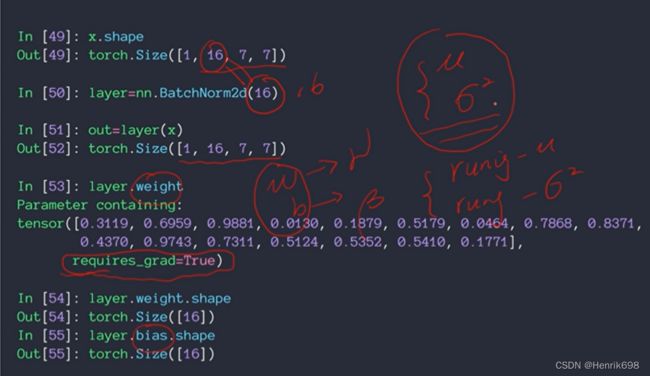
x = torch.rand(1,16,7,7)
# print(x)
print(x.shape)

layer = nn.BatchNorm2d(16) #这里的参数16一定要和输入数据的channel匹配起来

out = layer(x) #这里进行normalize，将数据范围很大的数据压缩到(0,1)的范围内。
# print(out)
print(out.shape)

#(γ=1, β=0)是不产生任何影响的
γ = layer.weight
print(γ)
β = layer.bias
print(β)

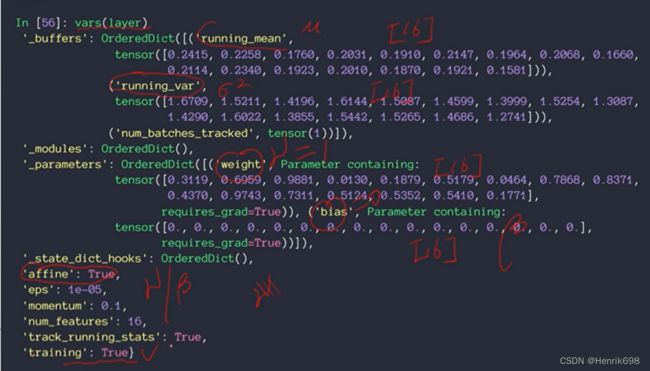
#这里需要注意一下：μ和σ²是没办法直接获取到的，只能查询总的均值和方差
running_μ = layer.running_mean #总的均值
print(running_μ)
running_σ = layer.running_var #总的方差
print(running_σ)

print('===========================')
#将当前layer的所有参数都打印出来
print(vars(layer))
#这四个参数（running_mean,running_var,weight,bias）都是维度为1，长度为16的
#这些参数中，'affine': True 表示γ(weight)和β(weight)需不需要自动衰减，如果是False,则weight就会自动设置为1，bias自动设置为0,且不自动更新和变换。
#'training' = True 表示当前的模式是train还是test。
#一般情况下affine和training都会设置为True。

Test

这里需要注意的是，和drop out一样，batch normalization这个layer在training和test情况下行为是不太一样的。

在training的时候，μ和σ会统计出来，并自动更新一下running，之后再反向传播（back propagation），更新一下γ和β。

在test的时候，一般我们只会test一个sample，因此μ和σ²是没法统计的，因为只有一个sample，所以就没有必要进行统计。因此在test的时候，μ和σ取的不是当前batch的μ和σ²，而在test的时候将全值running-μ和running-σ赋值为μ和σ²。此外在test的时候，是没有backward的，γ和β是不需要更新的。要实现test，就需要提前切换到test这个模式下，必须调用.eval()这个函数，设置为test模式，再调用BatchNorm1d()进行变换。

可视化Visualization

曲线图中的虚线是使用batch normalize的，实线的是没有使用的。
可以发现使用了batch normalize，收敛速度更快，精度也有所提升。我们可以查看每一层参数分布的情况，使用了后，其分布情况是围绕均值为0附近，总的来说会往0附近来靠近，并不一定是0，方差为1来进行分布，这样操作后更加利于training。这里需要注意一下，为什么不完完全全在以N(均值=0, 方差=1)这样进行分布呢？这是因为存在γ和β对其分布的调整，如果γ=1且β=0，那么其分布情况就不会是以N(均值=0, 方差=1)这样进行分布，其分布就是N(β为均值, γ为方差)这样的分布。

总结一下使用batch normalize的好处Advantage

▪ Converge faster
收敛速度更快，在使用sigmoid激活函数的时候，如果把数据限制到0均值单位方差，那么相当于只使用了激活函数中近似线性的部分，这显然会降低模型表达能力，但是收敛速度更快。

▪ Better performance
更加容易搜索出最优解

▪ Robust
▪ stable
变得更稳定了
▪ larger learning rate
更大的设置学习率的范围

五、经典卷积网络(CNN)

下图中是最近10年内的网络变化，其中柱状图上面的数字表示错误率（准确率=1-错误率）。

LeNet-5

在1989年，Yann LeCun提出了一种用反向传导进行更新的卷积神经网络，称为LeNet。
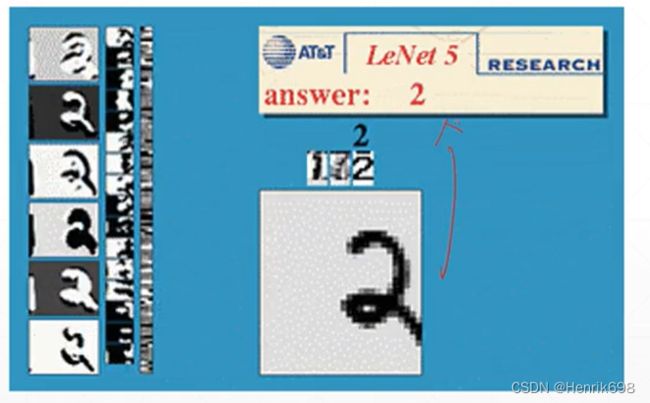
最开始的LeNet-5是用于一个手写数字的识别，手写数字的图片只有28*28，当时的网络结构并不深，而且每一层的参数量也不大，即使这样这个网络结构也是没有办法在GPU上跑的，因为当时GPU还没有，是386的年代。
这个准确度达到了99.2%，就可以很成熟的使用起来了。

所以在当时美国的支票票号识别，邮编识别就已经广泛使用了。

AlexNet

LeNet-5是80年代出来的，那个时候deep learning还没有很热，在2012年，出来了AlexNet，准确率有了很高的提升。当时是使用两个GTX580（3GB）显卡来进行该网络的运算，该网络是5个卷积层，总共是8个layers，AlexNet的小窗口是11*11的，此外第一次使用ReLU函数、Max pooling、Dropout。

VGG

VGGNet是来自于牛津大学的视觉研究组。VGG一共有6个版本（比如VGG11、VGG16、VGG19）。VGG探索出了，小的kernal窗口不但可以减少计算量，并且没有损害精度，而且计算速度很快，这也是VGG最核心的价值。探索出了更小型的kernal更好的效果。

这里我们先了解一下1*1卷积核：
1*1 Convolution
可以注意到的是，输入的channel是32，而到了输出channel就是16了。这里的输出的channel取决于kernal的channel。此外1*1的kernal可以保证输入和输出的图片大小是一样的。

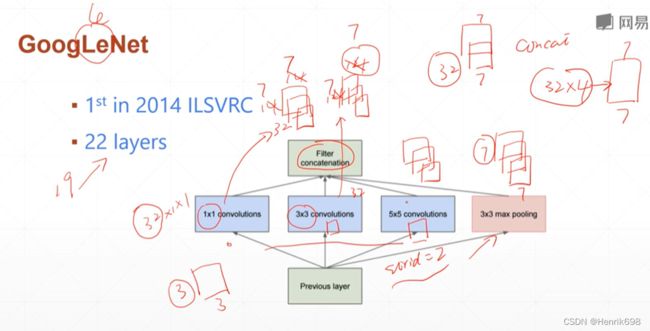
GoogLeNet

这里有不同大小的kernal，此外还有一个合并的操作Filter concatenation，为满足这个操作的要求，需要确保所有不同kernal输出来的图像大小相同，因为有一个33 max pooling，所有输出来的图像大小要与max pooling输出来的相同即可。假设max pooling输出的是77的图像，则kernal输出的也必须是77（为了保证输出的是77，可以使用stride步长来控制），这样可以获得很多个（32,7,7），之后通过concatenation操作后，可以获得（32,4，7,7）的feature map。

之前使用的都是统一的kernal，而这里为什么要使用不同类型的kernal呢？这是因为每一个不同大小的kernal所感受的视野是不同，11 kernal感受的视野是一个点，33 kernal感受的视野是一个小窗体，通过综合不同大小的视野（综合局部和全局的信息），可以感受到一个跟好的信息量。

具体的结构是：

堆叠更多层更好吗？Stack more layers?

通过堆叠更多层数的时候，层数更多的时候，反而准确度并没有提升，反而training比较困难，training的error比较高，这告诉我们并不能简单的堆叠更多的层数（这里需要抛开4层到22层，这范围内是堆叠更多层数效果会有提升，但是超过20层以上之后，仅是简单的堆叠的话，training的难度非常大，training找到最优解的难度很大）。

现在我们的网络结构以及是1000多层了，那如何解决这个问题的呢？也就是ResNet。

六、深度残差网络 ResNet

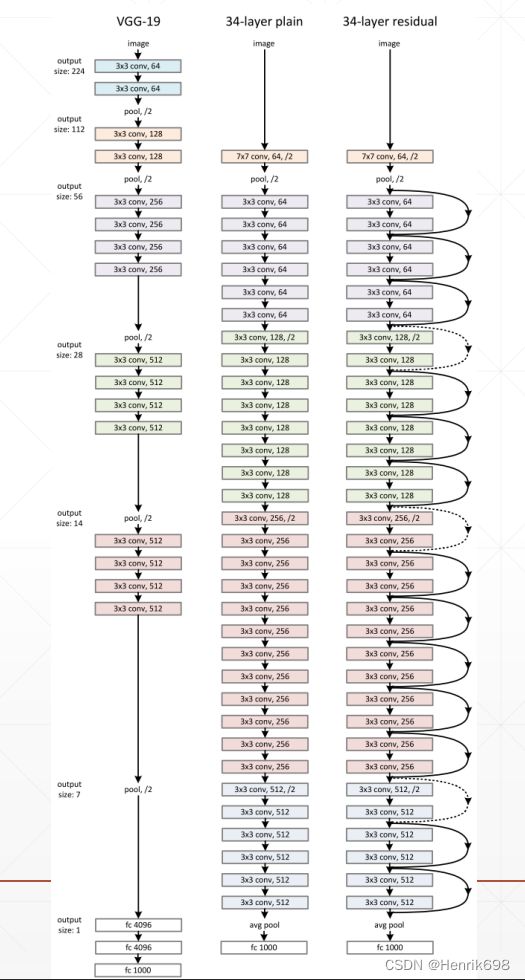
残差神经网络(ResNet)是由微软研究院的何恺明、张祥雨、任少卿、孙剑等人提出的。ResNet 在2015 年的ILSVRC（ImageNet Large Scale Visual Recognition Challenge）中取得了冠军。

残差神经网络的主要贡献是发现了“退化现象（Degradation）”，并针对退化现象发明了 “快捷连接（Shortcut connection）”，极大的消除了深度过大的神经网络训练困难问题。神经网络的“深度”首次突破了100层、最大的神经网络甚至超过了1000层。

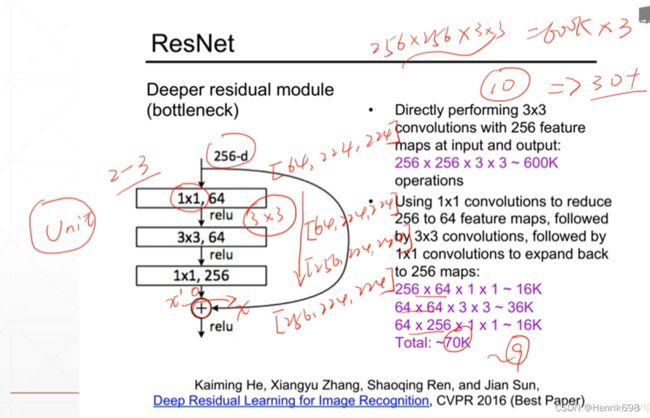
ResNet构建块Unit，选择什么样的结构合适

这个Unit选择一个2-3层的卷积层，再加一个short。为了能够shortcut，就意味着经过shortcut输出的结果要与输入时的维度相同且channel也不能衰减，即输入时256层，则shortcut时也要是256层。

我们来计算一下参数量，输出256，输入256，每一个kernal是33，则参数量大概有25625633 = 589,824 大约有600k左右。如果有三个这样的Convolution的话，还需要再乘以3。

所以为了减少这个参数量，将unit中的kernal的size减小。比如说输入时是(256,224,224)，通过第一个11 kernal时的结果是(64,224,224)；再通过第二个33 kernal时，进行padding处理后保持shape不变，依然是(64,224,224)；最后通过第三个1*1 kernal后，将输出结果恢复到原来的(256,224,224)。

输入时一个(256,224,224)，和shortcut的(256,224,224)进行对应元素位置的相加，同样大小的矩阵相加，是同位置直接相加，不改变其维度，最后结果也是(256,224,224)，是没有改变的。

再来计算一下参数量，2566411 ~ 16k；646433 ~ 36k；642561*1 ~ 16k；这样总共 Total是大约70k。和原来的600k参数量相比，大概少了9倍。

查看一下34层的ResNet的基本结构：

ResNet的爆炸性的效果

Why call Residual? 为什么叫残差呢？

F(x)表示unit卷积层学习的内容，原来学习的是H(x)，F(x) + x = H(x) 原来学习的情况。
对于unit中的卷积层来说，F(x) = H(x) - x。这个减号就是残差的由来。

跨时间维度上不同网络的比较

对于一个ResNet是如何实现的呢？

这里关键是如何实现一个Unit基本单元。

这里需要注意的是，我们可以将输入数据的channel和输出数据的channel设置成为不同的，我们只需在shortcut路径上增加一个1*1 kernal 将输入的channel通过这个kernal的channel进行调整，从而将输入的channel和输出channel有相同的数量。在shortcut的路径上增加一个调整channel的kernal，就可以不用担心输入和输出channel不同的问题了。

ResNet例子：

import  torch
from    torch import  nn
from    torch.nn import functional as F
from    torch.utils.data import DataLoader
from    torchvision import datasets
from    torchvision import transforms
from    torch import nn, optim

# from    torchvision.models import resnet18

class ResBlk(nn.Module):
    """
    resnet block
    """

    def __init__(self, ch_in, ch_out):
        """
        :param ch_in:
        :param ch_out:
        """
        super(ResBlk, self).__init__()

        self.conv1 = nn.Conv2d(ch_in, ch_out, kernel_size=3, stride=1, padding=1)
        self.bn1 = nn.BatchNorm2d(ch_out)
        self.conv2 = nn.Conv2d(ch_out, ch_out, kernel_size=3, stride=1, padding=1)
        self.bn2 = nn.BatchNorm2d(ch_out)

        self.extra = nn.Sequential()
        if ch_out != ch_in:
            # [b, ch_in, h, w] => [b, ch_out, h, w]
            self.extra = nn.Sequential(
                nn.Conv2d(ch_in, ch_out, kernel_size=1, stride=1),
                nn.BatchNorm2d(ch_out)
            )


    def forward(self, x):
        """
        :param x: [b, ch, h, w]
        :return:
        """
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))
        # short cut.
        # extra module: [b, ch_in, h, w] => [b, ch_out, h, w]
        # element-wise add:
        out = self.extra(x) + out

        return out




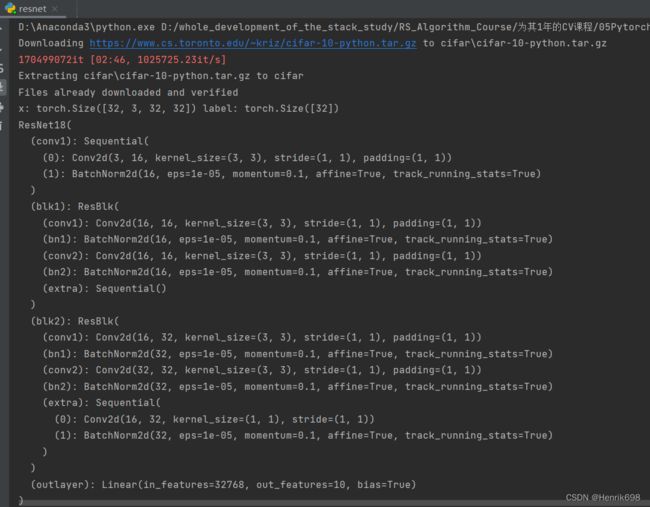
class ResNet18(nn.Module):

    def __init__(self):
        super(ResNet18, self).__init__()

        self.conv1 = nn.Sequential(
            nn.Conv2d(3, 16, kernel_size=3, stride=1, padding=1),
            nn.BatchNorm2d(16)
        )
        # followed 4 blocks
        # [b, 64, h, w] => [b, 128, h ,w]
        self.blk1 = ResBlk(16, 16)
        # [b, 128, h, w] => [b, 256, h, w]
        self.blk2 = ResBlk(16, 32)
        # # [b, 256, h, w] => [b, 512, h, w]
        # self.blk3 = ResBlk(128, 256)
        # # [b, 512, h, w] => [b, 1024, h, w]
        # self.blk4 = ResBlk(256, 512)

        self.outlayer = nn.Linear(32*32*32, 10)

    def forward(self, x):
        """
        :param x:
        :return:
        """
        x = F.relu(self.conv1(x))

        # [b, 64, h, w] => [b, 1024, h, w]
        x = self.blk1(x)
        x = self.blk2(x)
        # x = self.blk3(x)
        # x = self.blk4(x)

        # print(x.shape)
        x = x.view(x.size(0), -1)
        x = self.outlayer(x)


        return x



def main():
    batchsz = 32

    cifar_train = datasets.CIFAR10('cifar', True, transform=transforms.Compose([
        transforms.Resize((32, 32)),
        transforms.ToTensor()
    ]), download=True)
    cifar_train = DataLoader(cifar_train, batch_size=batchsz, shuffle=True)

    cifar_test = datasets.CIFAR10('cifar', False, transform=transforms.Compose([
        transforms.Resize((32, 32)),
        transforms.ToTensor()
    ]), download=True)
    cifar_test = DataLoader(cifar_test, batch_size=batchsz, shuffle=True)


    x, label = iter(cifar_train).next()
    print('x:', x.shape, 'label:', label.shape)

    device = torch.device('cuda')
    # model = Lenet5().to(device)
    model = ResNet18().to(device)

    criteon = nn.CrossEntropyLoss().to(device)
    optimizer = optim.Adam(model.parameters(), lr=1e-3)
    print(model)

    for epoch in range(1000):

        model.train()
        for batchidx, (x, label) in enumerate(cifar_train):
            # [b, 3, 32, 32]
            # [b]
            x, label = x.to(device), label.to(device)

            logits = model(x)
            # logits: [b, 10]
            # label:  [b]
            # loss: tensor scalar
            loss = criteon(logits, label)

            # backprop
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()


        #
        print(epoch, 'loss:', loss.item())


        model.eval()
        with torch.no_grad():
            # test
            total_correct = 0
            total_num = 0
            for x, label in cifar_test:
                # [b, 3, 32, 32]
                # [b]
                x, label = x.to(device), label.to(device)

                # [b, 10]
                logits = model(x)
                # [b]
                pred = logits.argmax(dim=1)
                # [b] vs [b] => scalar tensor
                correct = torch.eq(pred, label).float().sum().item()
                total_correct += correct
                total_num += x.size(0)
                # print(correct)

            acc = total_correct / total_num
            print(epoch, 'acc:', acc)


if __name__ == '__main__':
    main()

DenseNet

基于ResNet的短接层思路，可以推广到，每一个unit都可以和前面所有层都有一个短接，这样就有了DenseNet。

这里需要注意的是，DenseNet的每一次短接过程，其实是一个concat过程，是将之前的所有信息进行综合，不是element wise的相加操作，这样会使得最后的channel越来越大，所以DenseNet对于channel的选择要设计的很精妙，舍得后面的channel不至于过大。

七、nn.Module（使用nn.Module的好处）

pytorch中使用非常广泛的类叫nn.Module。
nn.Module类是所有网络层的父类，当需要实现自己的一个层的时候就必须要继承这个父类。

Magic

▪ Every Layer is nn.Module
nn.Module在pytorch中是一个基本的父类，当要实现一个前项计算图的时候，如果继承了nn.Module就可以非常方便的使用现成的一些类：
比如说： ▪ nn.Linear
▪ nn.BatchNorm2d
▪ nn.Conv2d

▪ nn.Module nested in nn.Module
除了使用这些类以外，还可以嵌套nested，每个nn.Module后又可以嵌套nn.Module。

使用nn.Module的好处

1、embed current layers

在nn.Module中启用了大量现成的神经网络计算的模块。使用这些现成的模块非常方便，只需要调用初始函数，再通过.__call__方法调用forward函数，就可以使用这个模块提供的功能了。
比如: ▪ Linear
▪ ReLU
▪ Sigmoid
▪ Conv2d
▪ ConvTransposed2d
▪ Dropout
▪ etc.

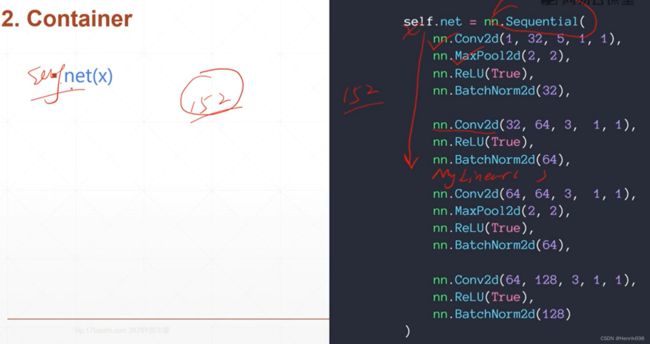
2、Container容器

Container就是nn.Sequential()这个类。
nn.Sequetial：按顺序包装多个网络层(使用容器的时候，容器里面的model属于容器，而这个容器属于本网络)注意哦，这个容器后面括号里都是参数所以要用逗号隔开。
sequential是一个时序模型，根据每个submodule传入的顺序写到计算图里，在forward的时候也会顺序执行。
self.net(x)就可以直接自动完成多次的forward的操作。

3、parameters 权值和偏置参数

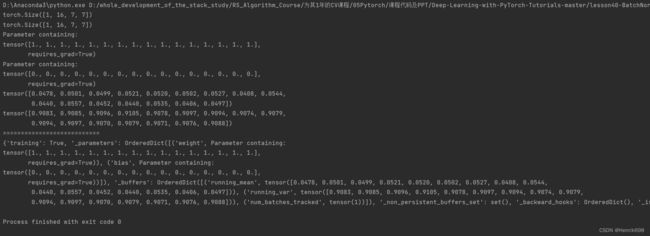
使用nn.Module可以很好的对模型参数进行管理，named_parameters()/parameters()方法，这两个方法都会返回一个用于迭代模型参数的迭代器（named_parameters还包括参数名字）。

比如说下图中使用Container容器，将两个线性层容在一起，名为net；通过net.parameters()这个方法可以返回一个生成器，其保存着每层的weight权值和bias偏置。

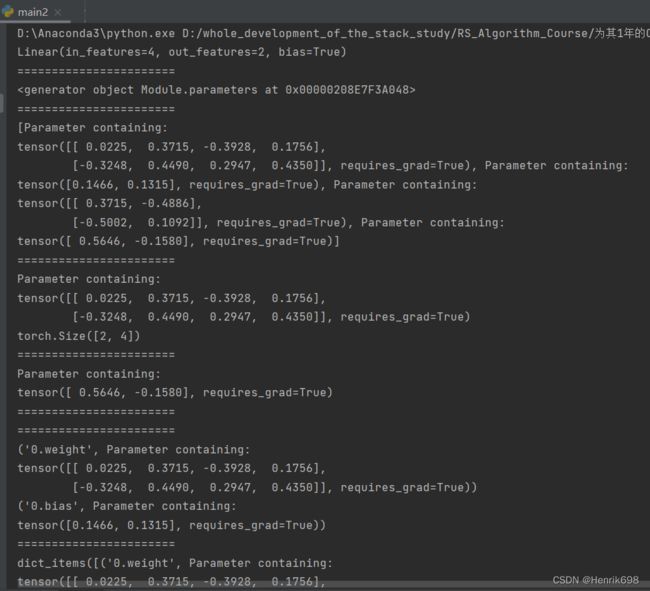
import torch
from torch import nn
print(nn.Linear(4,2))
print('=======================')
net = nn.Sequential(nn.Linear(4,2),nn.Linear(2,2))
# torch.nn.Linear(in_features, # 输入的神经元个数
#            out_features, # 输出神经元个数
#            bias=True # 是否包含偏置
#            )
print(net.parameters())
print('=======================')
print(list(net.parameters()))
print('=======================')
print(list(net.parameters())[0])
print(list(net.parameters())[0].shape)
#这里为什么是(2,4)呢？因为w是输出维度在前面，所以是(2,4)，是layer0的w。
print('=======================')
print(list(net.parameters())[3])
#这里是layer1的bias偏置，所以是(2)

print('=======================')
#通过.parameters可以很好的返回一个迭代器，返回当前这个net的所有参数。
#因此继承了nn.Module就不需要额外管理这些参数。
print('=======================')

#这个参数有两种形式，
# 一个是带名字的parameters，返回一个dictionary字典，字典第一个是名字，这个名字是pytorch自动生成的。
#这里我们将字典转换为了list。
#'0.weight' 表示第0层的weight
print(list(net.named_parameters())[0])
#'0.bias' 表示第0层的bias
print(list(net.named_parameters())[1])
print('=======================')
#这里我们以字典形式打印出来
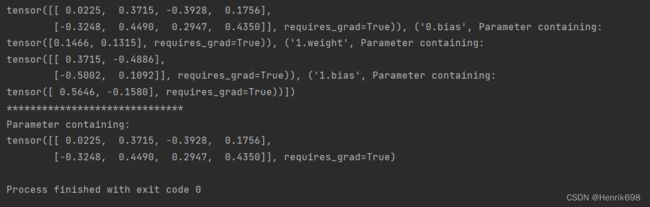
print(dict(net.named_parameters()).items())
#这里item()方法是返回这个字典中的所有属性
print('******************************')
#一个是不带名字的parameters。
print(list(net.parameters())[0])

#我们可以通过.parameter，将所有参数传入到优化器中。
#之前我们是通过[w1,b1,w2,b2]这种方式自己管理参数，将这些传入到optimizer中的。
#现在就直接将这个类的.parameters()传入其中即可，这样使用时非常非常方便的。

4. modules 查看子类

▪ modules: all nodes
对于内部的类可以做到很好的管理。所有的子节点可以称为modules。

▪ children: direct children
直接的子节点，我们称其为children。

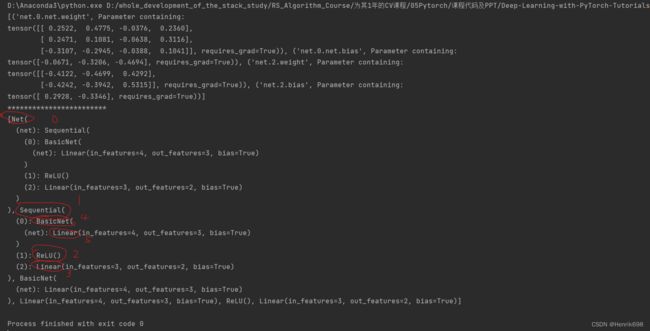
使用nn.modules()可以查看所有的子类情况。
其返回的是module其本身0号、其直系儿子1号和其它所有子节点。

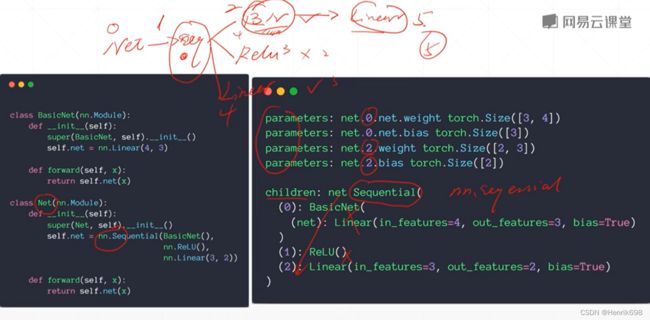
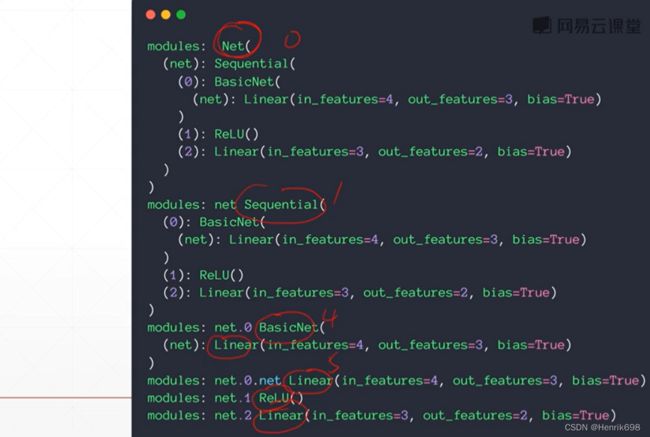
import torch
from torch import nn

class BasicNet(nn.Module):
    def __init__(self):
        super(BasicNet, self).__init__()
        self.net = nn.Linear(4, 3)

    def forward(self, x):
        return self.net(x)


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.net = nn.Sequential(BasicNet(), nn.ReLU(), nn.Linear(3, 2))

    def forward(self, x):
        return self.net(x)


net = Net()
print(list(net.named_parameters()))
print('************************')
print(list(net.modules()))

5、to(device) 切换GPU或CPU

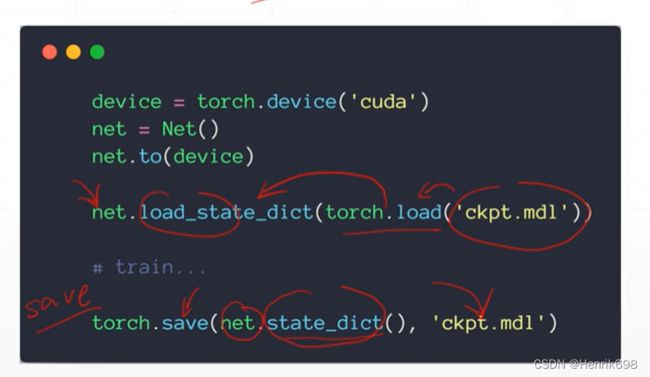
可以非常方便的将一个类所有的成员函数、所有内部的tensor和所有的操作转移到GPU或CPU上。

这里需要特别注意，当a是tensor类型时，a.to 返回的是 a_GPU，注意这里的a_GPU和原来的a.to的a不是同一个东西，a.to的a是CPU上的。而对于nn.Module来说，net = net.to。

6、save and load 保存和加载网络中间状态

在使用pytorch进行深度学习训练的时候，经常会有些内容需要保存下来，保存到硬盘张，不管什么时候我们都可以读取到，那么这个时候，使用torch.save()就可以将内容存储器来，使用torch.load()就可以将存取的内容读取出来。
save and load保存和加载 Checkpoint 用于推理/继续训练，Checkpoint是网络的中间状态。
保存和加载是可以用于在断电等特殊情况下，不至于失去之前训练的结果，避免让其从头开始从新训练。

Save操作：

#save:
torch.save(net.state_dict(), 'ckpt.mdl')

Load操作：

net.load_state_dict(torch.load('ckpt.mdl'))

7、train / test 切换

train和test的方便切换状态。如果每个类都继承与nn.Module的话，直接通过对根节点net.train()，或.eval()，就可以切换了。

8、implement own layer 实现自己的类

比如说在pytorch中没有一个展平的功能Flatten，因此我们可以自己实现一个继承与nn.Module的用于展平功能的类。
此外还有一个是reshape操作，这个功能只有方法，没有一个类，所以很多情况下我们也需要自己创建一个继承与nn.Module的用于Reshape的类。

class Flatten(nn.Module):
    def __init__(self):
        super(Flatten, self).__init__()
    
    def forward(self, input):
        return input.view(input.size(0), -1)

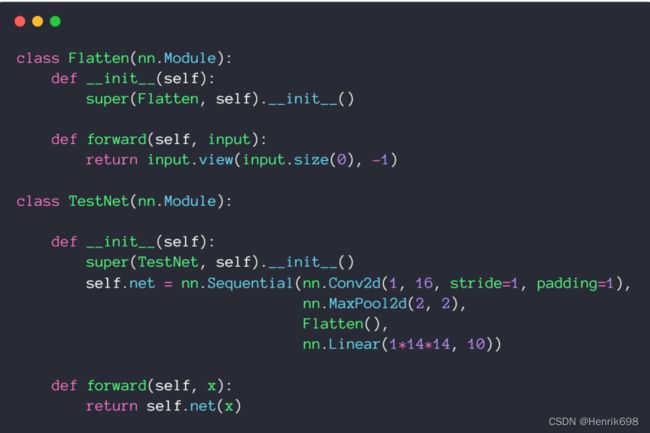
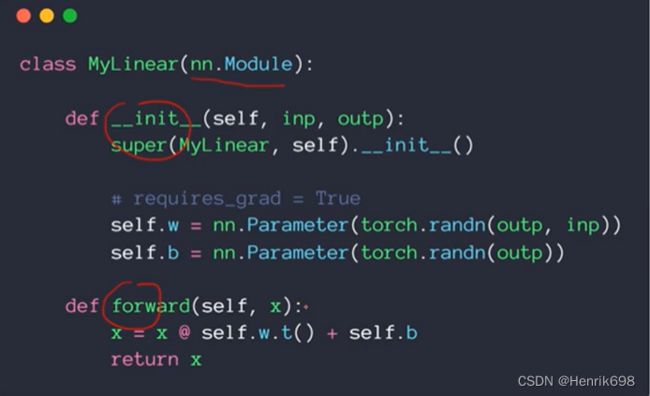
实现一个自己的MyLinear，这个自己创建的类和nn.Linear功能是一样的，这里可以发现nn.Parameter()会自动将需要梯度设置为true，requires_grad=True，而且参数也会受到nn.parameters()的管理，注意类是大写的Parameter，方法是小写的parameters。
我们在forward()函数中写好我们的逻辑，再return，一定要返回。

class MyLinear(nn.Module):
    def __init__(self, inp, outp):
        super(MyLinear, self).__init__()
        
        #requires_grad = True
        self.w = nn.Parameter(torch.randn(outp,inp))
        self.b = nn.Parameter(torch.randn(outp))
        
    def forward(self,x):
        x = x @ self.w.t() + self.b
        return x

八、数据增强（Data Argumentation）

Big Data

很大的数据集是train的好坏的前提。有了Big Data神经网络就能train的很好，有了Big Data这个网络就不容易over fitting，这个是防止过拟合的关键The key to prevent Overfitting。

Limited Data 有限的数据进行优化

▪ Small network capacity
首先如果数据比较少的话，就要减少网络的参数量，这样就不容易overfitting。

▪ Regularization
如果网络结构是固定的话，我们就正则化Regularization，迫使网络的一部分权值w接近于0，这样也减少了网络的参数量。

▪ Data argumentation
对原来的数据进行增强，比如对原来的图像进行调色，旋转角度等，获得新的图片，将这些图片和原先的图片一起用于网络的训练。

Data argumentation

▪ Flip 翻转
▪ Rotate 旋转
▪ Scale 缩放
▪ Crop Part 裁剪部分
▪ Noise 白噪声
▪ Random Move 随机移动
▪ GAN 生成对抗网络

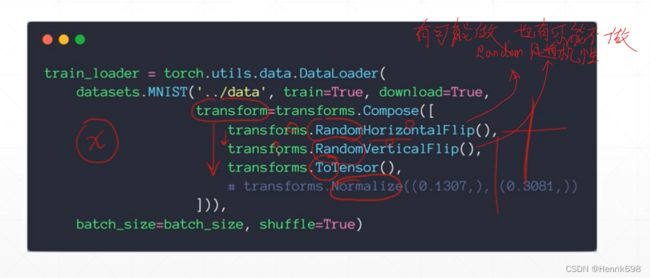
Flip翻转

水平翻转和竖直翻转：

.RandomHorizontalFlip()水平翻转、.RandomVerticalFlip()竖直翻转，这两个都是随机的，有可能做，也有可能不做。

Rotate旋转

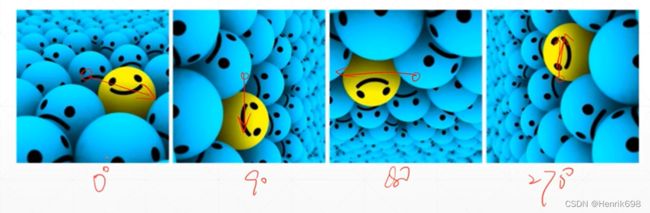
.RandomRotation(15)会在-15°<0<15°会在个区间内随机的进行选择；如果我们要固定这个角度，.RandomRotation([0, 90, 180, 270])会随机的在0°、90°、180°和270°三个角度中选取进行旋转，如果要不旋转的那就在加一个0°，这样会将原来的照片数量变为原来的4被。

Scale缩放

Crop Part裁剪部分

随机裁剪一部分，裁切的那部分用0来填补。

Noise白噪声

pytorch没有提供这个Noise接口，需要人为在Numpy基础上添加这个。

这里需要总结一下数据增强，由于增强后的照片与原图片是比较接近的，所有数据增强是有一定的帮助的，但是帮助不会很多。