神经网络学习笔记(三)——长短期记忆网络LSTM

长短期记忆网络 LSTM

一、概述

  长短期记忆网络——通常被称为LSTM，是一种特殊的RNN，能够学习长期依赖性。由Hochreiter和Schmidhuber（1997）提出，并且在接下来的工作中被许多人改进和推广。LSTM 在各种各样的问题上表现非常出色，现在被广泛使用。LSTM被明确设计用来避免长期依赖性问题。LSTM单元由单元，输入门，输出门和忘记门组成。该单元记住任意时间间隔内的值，并且三个门控制进出单元的信息流。

  LSTM网络非常适合基于时间序列数据进行分类，处理和预测，因为在时间序列中的重要事件之间可能存在未知持续时间的滞后。开发LSTM是为了处理在训练传统RNN时可能遇到的爆炸和消失的梯度问题。对于间隙长度的相对不敏感性是LSTM相对于RNN，隐马尔可夫模型和其他序列学习方法在许多应用中的优势。

二、背景

  传统RNN的关键点之一就是他们可以用来连接先前的信息到当前的任务上，例如使用过去的视频段来推测对当前段的理解。但是会有一些复杂的场景。上下文距离预测词较远，即相关信息和当前预测位置之间的间隔相当的大，在这个间隔不断增大时，传统RNN会丧失学习到连接如此远的信息的能力。

  循环神经网络中的LSTM可以解决这种问题，即长短期记忆网络。LSTM引入了门（gate）机制用于控制特征的流通和损失，其中输入门用来接受近期有用的信息，遗忘门用来对久远的、无用的信息选择性的遗忘，输出门的输出为根据当前状态决定的输出。可以解决RNN无法处理长距离的依赖的问题。

三、LSTM原理

3.1 模型结构

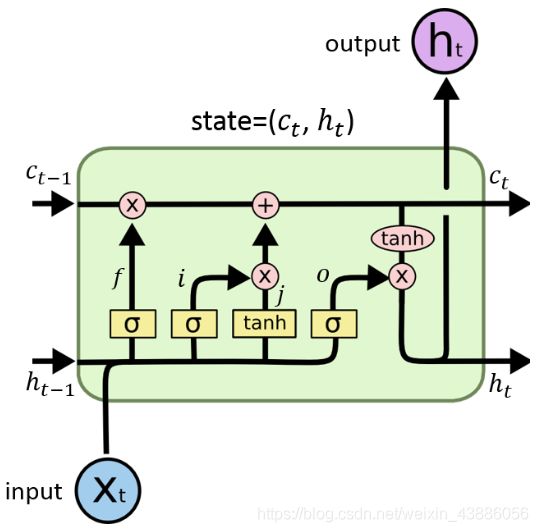
  原始RNN的隐藏层只有一个状态h，对于短期的输入非常敏感。LSTM再增加一个状态c，用来保存长期的状态，称为单元状态(cell state)。

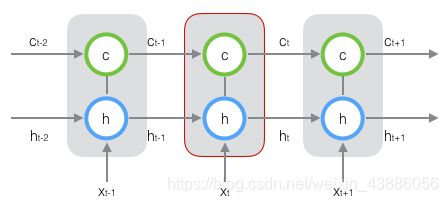
  在$t$时刻，LSTM的输入有三个：

• 当前时刻网络的输入值$x_t$
• 上一时刻LSTM的输出值 $h_{t-1}$
• 上一时刻的单元状态$c_{t-1}$

  LSTM的输出有两个：

• 当前时刻LSTM输出值$h_t$
• 当前时刻的单元状态$c_t$

  在LSTM模型结构中，采用门(gate)来控制长期状态，在一层模型里有三个门，分别作用为：

• 负责控制继续保存长期状态$c$
• 负责控制把即时状态输入到长期状态$c$
• 负责控制是否把长期状态$c$作为当前的LSTM的输出

  gate实际上就是一层全连接层，输入是一个向量，输出是一个0到1之间的实数向量。公式为：$g(x)=\sigma (Wx+b)$

3.2 前向传播

  LSTM每个模块中的具体结构如下：

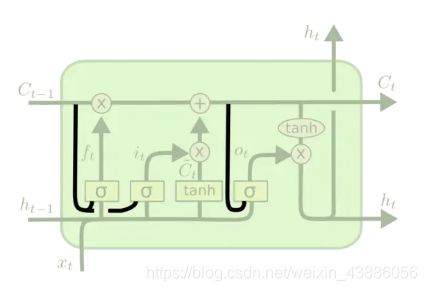
  遗忘门（forget gate）：决定了上一时刻的单元状态$c_{t-1}$如何保留到当前时刻 $c_t$。

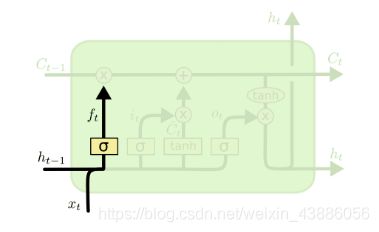
  遗忘阶段是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的，记住重要的”。

  具体来说是通过计算得到的$f_t$（f表示forget）来作为遗忘门控，来控制上一个状态的 $c_{t-1}$的忘记的概率。
$$f_t=\sigma (W_f\cdot [h_{t-1},x_t]+b_f)$$

  输入门（input gate）：决定了当前时刻网络的输入$x_t$如何保存到单元状态$c_t$。

  这个阶段确定什么样的新信息被存放在细胞状态中。这里包含两个部分：1）sigmoid层为 “输入门层” ，主要对输入$x_t$进行选择记忆。2）tanh层创建一个新的候选值向量${\tilde{C}}_t$，加入到状态中。
$$i_t=\sigma (W_i\cdot [h_{t-1},x_t]+b_i)$$

$${\tilde{C}}_t=\tanh (W_C\cdot [h_{t-1},x_t]+b_C)$$

  细胞更新（Update Cell）：决定了如何计算当前序列下的细胞值$C_t$。

  新的细胞状态由两部分组成，1）旧细胞$C_{t-1}$与$f_t$相乘，丢弃掉之前序列的信息；2）新的候选值${\tilde{C}}_t$与比例系数$i_t$的积，保留当前的输入信息。
$$C_t=f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t$$
  其中，$\odot$为Hadamard积

  输出门（output gate）：控制单元状态$C_t$有多少输出到LSTM的当前输出值$h_t$。

  隐藏状态$h_t$的更新由两部分组成：1）$o_t$, 它由上一序列的隐藏状态$h_{t-1}$和输入数据$x_t$构成，通过激活函数sigmoid进行过滤；2）由隐藏状态$C_t$和tanh函数构成，tanh将$C_t$处理得到一个在$(-1,1)$之间的值，然后将其与sigmoid门相乘得到$h_t$。
$$o_t=\sigma (W_o\cdot [h_{t-1},x_t]+b_o)$$

$$h_t=o_t\odot \tanh (C_t)$$

3.3 反向传播

  算法框架：采用反向传播算法

• 前向计算每个神经元的输出值，即$f_t$、$i_t$、$c_t$、$o_t$、$h_t$五个向量的值。
• 反向计算每个神经元的误差项$\delta$值。包括两个方向：1）沿时间的反向传播，即从当前$t$时刻开始，计算每个时刻的误差项；2）将误差项向上一层传播。
• 根据相应的误差项，计算每个权重的梯度。

  对于激活函数，先求出其导数：
$$\sigma (z)\stackrel{\underset{def}{}}{=}y=\frac{1}{1+e^{-z}}\Rightarrow {\sigma }^{\prime }(z)=y(1-y)$$

$$\tanh (z)\stackrel{\underset{def}{}}{=}y=\frac{e^z-e^{-z}}{e^z+e^{-z}}\Rightarrow {\tanh }^{\prime }(z)=1-y^2$$

  在$t$时刻，LSTM的输出值为$h_t$，定义此时的误差项${\delta }_t$为
$${\delta }_t\stackrel{\underset{def}{}}{=}\frac{\partial L}{\partial h_t}$$

  误差项沿时间的反向传递

$${\delta }_{t-1}^T=\frac{\partial L}{\partial h_{t-1}}=\frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial h_{t-1}}={\delta }_t^T\frac{\partial h_t}{\partial h_{t-1}}$$

  误差项沿时间的反向传递
  由于有$h_t=o_t\odot \tanh (C_t)$和$$C_t=f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t$$，利用全导数，计算得出
$${\delta }_{t-1}={\delta }_{o,j}^T{W}_{oh}+{\delta }_{f,j}^T{W}_{fh}+{\delta }_{i,j}^T{W}_{ih}+{\delta }_{{\tilde{C}}_t,j}^T{W}_{Ch}$$
  又因为有
$$\{\begin{array}{l}{\delta }_{o,t}^T={\delta }_t^T\odot \tanh (C_t)\odot o_t\odot (1-o_t)\\ {\delta }_{f,t}^T={\delta }_t^T\odot o_t\odot (1-\tanh (C_t{)}^2)\odot C_{t-1}\odot f_t\odot (1-f_t)\\ {\delta }_{i,t}^T={\delta }_t^T\odot o_t\odot (1-\tanh (C_t{)}^2)\odot {\tilde{C}}_t\odot i_t\odot (1-i_t)\\ {\delta }_{{\tilde{C}}_t,t}^T={\delta }_t^T\odot o_t\odot (1-\tanh (C_t{)}^2)\odot i_t\odot (1-{{\tilde{C}}_t}^2)\end{array}$$
  带入上式可得出
$${\delta }_k^T=\prod _{j=k}^{t-1}{\delta }_{o,j}^T{W}_{oh}+{\delta }_{f,j}^T{W}_{fh}+{\delta }_{i,j}^T{W}_{ih}+{\delta }_{{\tilde{C}}_t,j}^T{W}_{Ch}$$

  将误差项传递到上一层

  如果当前层为第$l$层，设$l-1$层的误差项是误差函数对$l-1$层加权输入的导数：
$${\delta }_t^{l-1}\stackrel{\underset{def}{}}{=}\frac{\partial L}{ne{t}_t^{l-1}}$$
  则LSTM的输入可以表示为：
$$x_t^l=f^{l-1}(ne{t}_T^{l-1})$$
  其中$f^{l-1}$表示第$l-1$层的激活函数。
  将$ne{t}_t^{l-1}$展开，并利用全导数公式，得到
$$\frac{\partial L}{ne{t}_t^{l-1}}={\delta }_{f,t}^T{W}_{fx}+{\delta }_{i,t}^T{W}_{ix}+{\delta }_{\tilde{C},t}^T{W}_{Cx}+{\delta }_{o,t}^T{W}_{ox}\odot f^{\prime }(ne{t}_t^{l-1})$$

  权重梯度计算

  最终的梯度值为各个时刻的梯度之和：
$$\frac{\partial L}{\partial W_{oh}}=\sum _t\frac{\partial L}{\partial W_{oh,t}}=\frac{\partial L}{\partial ne{t}_{o,t}}\frac{\partial ne{t}_{o,t}}{\partial W_{oh,t}}=\sum _t{\delta }_{o,j}{h}_{j-1}^T$$
  同理可求得其它梯度为
$$\{\begin{array}{l}\frac{\partial L}{\partial W_{fh}}={\sum }_t{\delta }_{f,j}{h}_{j-1}^T\\ \frac{\partial L}{\partial W_{ih}}={\sum }_t{\delta }_{i,j}{h}_{j-1}^T\\ \frac{\partial L}{\partial W_{Ch}}={\sum }_t{\delta }_{\tilde{C},j}{h}_{j-1}^T\end{array}$$

  对于偏置项$b$的梯度，按照同样的方式可以求得
$$\{\begin{array}{l}\frac{\partial L}{\partial b_o}={\sum }_t{\delta }_{o,j}\\ \frac{\partial L}{\partial b_i}={\sum }_t{\delta }_{i,j}\\ \frac{\partial L}{\partial b_f}={\sum }_t{\delta }_{f,j}\\ \frac{\partial L}{\partial b_C}={\sum }_t{\delta }_{C,j}\end{array}$$

  对于输入$x$的权重矩阵的梯度，只需要根据相应的误差项直接计算：
$$\{\begin{array}{l}\frac{\partial L}{\partial W_{ox}}={\delta }_{o,t}{x}_t^T\\ \frac{\partial L}{\partial W_{fx}}={\delta }_{f,t}{x}_t^T\\ \frac{\partial L}{\partial W_{ix}}={\delta }_{i,t}{x}_t^T\\ \frac{\partial L}{\partial W_{Cx}}={\delta }_{C,t}{x}_t^T\end{array}$$

3.4 LSTM的变体

3.4.1 Peephole Connection

  让门层也会接受细胞状态的输入。

$$\{\begin{array}{l}{f}_t=\sigma (W_f\cdot [C_{t-1},h_{t-1},x_t]+b_f)\\ i_t=\sigma (W_i\cdot [C_{t-1},h_{t-1},x_t]+b_i)\\ o_t=\sigma (W_o\cdot [C_{t-1},h_{t-1},x_t]+b_o)\end{array}$$

3.4.2 Coupled

  将遗忘门和输入门合二为一，一同做出决定。即仅仅会当将要输入在当前位置时遗忘；仅仅输入新值到已经遗忘旧信息的那些状态。

$$C_t=f_t\odot C_{t-1}+(1-f_t)\odot {\tilde{C}}_t$$

四、LSTM的简单使用

  在自然语言处理中，LSTM适合用于处理与时间序列高度相关的问题。相较于传统的RNN模型，LSTM对长期记忆的表现更好。利用nn.LSTM模型对语料进行了文本分类的处理。

  首先从文件中读取相应训练集和测试集的语料，利用jieba对文本进行分词，然后利用nltk去停用词。这里nltk_data中并没有中文的停用词，我从网上找了一个中文的停用词文件放在对应的stopwords目录下，并命名为chinese。

def tokenizer(text):
    sentence = jieba.lcut(text, cut_all=False)
    stopwords = stopwords.words('chinese')
    sentence = [_ for _ in sentence if _ not in stopwords]
    return sentence

  利用torchtext包处理预处理好的语料，将所提供的语料集转化为相应的词向量模型。由于每一个词均为一个向量，作为LSTM模型的输入。

train_set, validation_set = data.TabularDataset.splits(
            path='corpus_data/',
            skip_header=True,
            train='corpus_train.csv',
            validation='corpus_validation.csv',
            format='csv',
            fields=[('label', label), ('text', text)],
        )
text.build_vocab(train_set, validation_set)

  将处理好的词向量输入到lstm模型中进行处理。

self.lstm = nn.lstm(embedding_dim, self.hidden_size, batch_first=True)
self.linear = nn.Linear(self.hidden_size, label_num)
def forward(self, x):
    # 输入x的维度为(batch_size, max_len),
    x = self.embedding(x)  # 经过embedding,x的维度为(batch_size, time_step, embedding_dim)

    # 隐层初始化
    # h0,c0维度为(direction_num, batch_size, hidden_size)
    h0 = torch.rand(1, x.size(0), self.hidden_size)
    c0 = torch.zeros(1, x.size(0), self.hidden_size)
    # out维度为(batch_size, seq_length, hidden_size)
    out, (hn, cn) = self.lstm(x, (h0,c0))
    # 只需要最后一步的输出状态
    out = out[:, -1, :]
    out = self.linear(out)
    return out

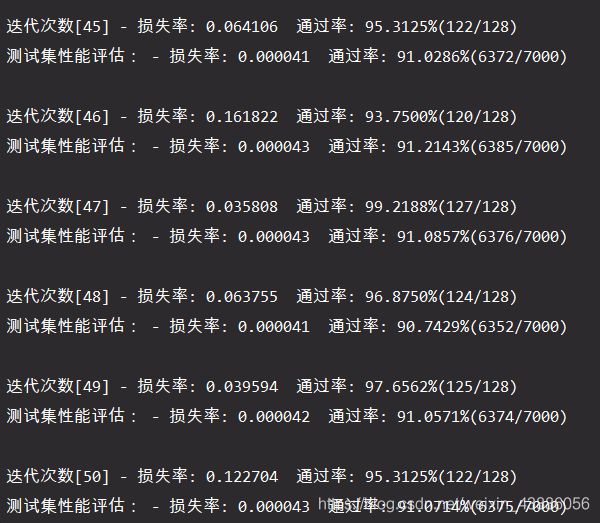
  利用训练集对模型进行训练，同时评估训练效果，并利用测试集对模型的准确性进行评估。为了防止偶然性产生的不确定，每一轮迭代会产生100个模型，分别评估其效率，进行调优后再用测试集测试其效率。

  在训练初期，准确率大概在50%左右。在第4轮迭代时准确率有显著提升，第5，6轮时基本能达到85%到90%准确度，收敛效果好于普通RNN。

  多轮迭代之后，模型的准确率可以达到90%以上。

五、总结

• 通过门控状态来控制传输状态，记住需要长时间记忆的，忘记不重要的信息，对很多需要“长期记忆”的任务来说，尤其好用。
• 门机制极大的减轻了梯度消失问题，简化了调参复杂度；门机制提供了特征过滤，丰富了向量的表示信息。
• 每个LSTM的cell里面都有4个全连接层，如果LSTM的时间跨度很大，并且网络又很深，则计算量会很大。
• 在语言处理任务中，LSTM非常适合用于处理与时间序列高度相关的问题，例如机器翻译、对话生成、编码\解码等。