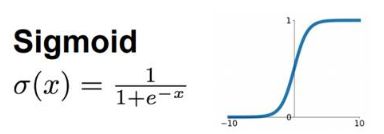- LeetCode 148. 排序链表:归并排序的细节解析
进击的小白菜
2025Top100详解leetcode链表算法
文章目录题目描述一、方法思路:归并排序的核心步骤二、关键实现细节:快慢指针分割链表1.快慢指针的初始化问题2.为什么选择`fast=head.next`?示例1:链表长度为偶数(`1->2->3->4`)三、完整代码实现四、复杂度分析五、总结题目描述LeetCode148题要求对链表进行排序,时间复杂度需为O(nlogn),且空间复杂度为O(logn)。由于链表的特殊结构(无法随机访问),归并排序
- PyTorch & TensorFlow速成复习:从基础语法到模型部署实战(附FPGA移植衔接)
阿牛的药铺
算法移植部署pytorchtensorflowfpga开发
PyTorch&TensorFlow速成复习:从基础语法到模型部署实战(附FPGA移植衔接)引言:为什么算法移植工程师必须掌握框架基础?针对光学类产品算法FPGA移植岗位需求(如可见光/红外图像处理),深度学习框架是算法落地的"桥梁"——既要用PyTorch/TensorFlow验证算法可行性,又要将训练好的模型(如CNN、目标检测)转换为FPGA可部署的格式(ONNX、TFLite)。本文采用"
- Linux/Centos7离线安装并配置MySQL 5.7
有事开摆无事百杜同学
LInux/CentOS7linuxmysql运维
Linux/Centos7离线安装并配置MySQL5.7超详细教程一、环境准备1.下载MySQL5.7离线包2.使用rpm工具卸载MariaDB(避免冲突)3.创建系统级别的MySQL专用用户二、安装与配置1.解压并重命名MySQL目录2.创建数据目录和配置文件3.设置目录权限4.初始化MySQL5.配置启动脚本6.配置环境变量三、启动与验证1.启动MySQL服务2.获取初始密码3.登录并修改密码
- 初始化列表与类型转换(C++)
2401_89195731
c++开发语言
初始化列表和构造函数体在C++中都是用于给类的成员变量赋初值区别:初始化列表是给每个成员变量定义初始化的地方,即使有成员变量没有给它显式在初始化列表初始化,它也会走初始化列表初始化时机初始化列表:在对象创建时,成员变量通过初始化列表被直接初始化,这发生在构造函数体执行之前。构造函数体内赋值:成员变量首先被默认初始化,然后在构造函数体内通过赋值语句进行赋值。性能差异初始化列表:通常更高效,因为它避免
- list的一些特性(C++)
2401_89195731
c++开发语言
C++STL库中的std::list是一个带头双向循环链表,使用之前需要包头文件,它和vector的使用高度类似。构造list支持多种构造方式默认构造函数:创建一个空的列表。拷贝构造函数:从另一个相同类型的列表创建一个新的列表。范围构造函数:从一对迭代器指定的范围内复制元素到新的列表中。初始值列表构造函数:使用初始化列表(initializerlist)创建一个包含指定元素的列表。填充构造函数:创
- 深度学习模型表征提取全解析
ZhangJiQun&MXP
教学2024大模型以及算力2021AIpython深度学习人工智能pythonembedding语言模型
模型内部进行表征提取的方法在自然语言处理(NLP)中,“表征(Representation)”指将文本(词、短语、句子、文档等)转化为计算机可理解的数值形式(如向量、矩阵),核心目标是捕捉语言的语义、语法、上下文依赖等信息。自然语言表征技术可按“静态/动态”“有无上下文”“是否融入知识”等维度划分一、传统静态表征(无上下文,词级为主)这类方法为每个词分配固定向量,不考虑其在具体语境中的含义(无法解
- git cherry-pick使用教程
gitcherry-pick使用教程发版分支命名格式release-20241009单次commit命名格式【功能点概括】-开发人员名称-详细内容例如:【项目初始化】-眸廓-初始化项目代码,用于开发源分支gitcherry-pick功能简介gitcherry-pick是用来从一个分支中选择一个或多个特定的提交,并将这些提交应用到当前分支。这样可以只选择需要的更改,而不是合并整个分支。gitcher
- C++STL-set
s15335
C++STLc++开发语言
一.基础概念set也是一种容器,像vector,string这样,但它是树形容器。在物理结构上是二叉搜索树,逻辑上还是线性结构。set容器内元素不可重复,multiset内容器元素可以重复;这两个容器,插入的元素都是有序排列。二.基础用法1.set对象创建1.默认构造函数sets1;2.初始化列表sets2_1={9,8,7,6,5};//56789sets2_2({9,8,7,7,6,5});/
- 老系统改造增加初始化,自动化数据源配置(tomcat+jsp+springmvc)
老系统改造增加初始化,自动化数据源配置一、前言二、改造描述1、环境说明2、实现步骤简要思考三、开始改造1、准备sql初始化文件2、启动时自动读取jdbc文件,创建数据源,如未配置,需要一个默认的临时数据源2.1去掉spingmvc原本配置的固定dataSource,改为动态dataSource2.2代码类,这里是示例,我就不管规范了,放到一起2.2.1DynamicDataSourceConfig
- 面试官:Spring 如何控制 Bean 的加载顺序?
在大多数情况下,我们不需要手动控制Bean的加载顺序,因为Spring的IoC容器足够智能。核心原则:依赖驱动加载SpringIoC容器会构建一个依赖关系图(DependencyGraph)。如果BeanA依赖于BeanB(例如,A的构造函数需要一个B类型的参数),Spring会保证在创建BeanA之前,BeanB已经被完全创建和初始化好了。@ServicepublicclassServiceA{
- 【Qualcomm】高通SNPE框架简介、下载与使用
Jackilina_Stone
人工智能QualcommSNPE
目录一高通SNPE框架1SNPE简介2QNN与SNPE3Capabilities4工作流程二SNPE的安装与使用1下载2Setup3SNPE的使用概述一高通SNPE框架1SNPE简介SNPE(SnapdragonNeuralProcessingEngine),是高通公司推出的面向移动端和物联网设备的深度学习推理框架。SNPE提供了一套完整的深度学习推理框架,能够支持多种深度学习模型,包括Pytor
- 学习日记-spring-day45-7.10
永日45670
学习springjava
知识点:1.初始化Bean单例池完成getBeancreateBean(1)知识点核心内容重点单例词初始化在容器初始化阶段预先创建单例对象,避免在getBean时动态创建单例词必须在容器初始化时完成加载,否则会触发异常getBean方法逻辑1.从beanDefinitionMap查询BeanDefinition2.根据scope判断单例/多例3.单例:直接从单例词获取4.多例:反射动态创建新对象多
- 深度学习篇---昇腾NPU&CANN 工具包
Atticus-Orion
上位机知识篇图像处理篇深度学习篇深度学习人工智能NPU昇腾CANN
介绍昇腾NPU是华为推出的神经网络处理器,具有强大的AI计算能力,而CANN工具包则是面向AI场景的异构计算架构,用于发挥昇腾NPU的性能优势。以下是详细介绍:昇腾NPU架构设计:采用达芬奇架构,是一个片上系统,主要由特制的计算单元、大容量的存储单元和相应的控制单元组成。集成了多个CPU核心,包括控制CPU和AICPU,前者用于控制处理器整体运行,后者承担非矩阵类复杂计算。此外,还拥有AICore
- 深度学习图像分类数据集—桃子识别分类
AI街潜水的八角
深度学习图像数据集深度学习分类人工智能
该数据集为图像分类数据集,适用于ResNet、VGG等卷积神经网络,SENet、CBAM等注意力机制相关算法,VisionTransformer等Transformer相关算法。数据集信息介绍:桃子识别分类:['B1','M2','R0','S3']训练数据集总共有6637张图片,每个文件夹单独放一种数据各子文件夹图片统计:·B1:1601张图片·M2:1800张图片·R0:1601张图片·S3:
- 使用 Deepseek Zero Coding Experience 创建类似飞扬的小鸟游戏
知识大胖
NVIDIAGPU和大语言模型开发教程游戏deepseekollamajanuspro
简介Flappybird在苹果商店推出后,每天大约能赚5000美元,但后来被苹果故意下架。现在我正尝试使用Deepseek制作这样一款游戏。技术在不断变化,编码知识也在不断变化,只需修改代码即可获得结果。让我们在Deepseek上试试这款游戏:推荐文章《如何在本地电脑上安装和使用DeepSeekR-1》权重1,DeepSeek《Nvidia系列之使用NVIDIAIsaacSim和ROS2的命令行控
- 在 Obsidian 中本地使用 DeepSeek — 无需互联网!
知识大胖
NVIDIAGPU和大语言模型开发教程人工智能deepseek
简介您是否想在Obsidian内免费使用类似于ChatGPT的本地LLM?如果是,那么本指南适合您!我将引导您完成在Obsidian中安装和使用DeepSeek-R1模型的确切步骤,这样您就可以在笔记中拥有一个由AI驱动的第二大脑。推荐文章《24GBGPU中的DeepSeekR1:UnslothAI针对671B参数模型进行动态量化》权重1,DeepSeek类《在RaspberryPi上运行语音识别
- OpenWebUI系列之 如何通过docker自动将其更新到OpenWebUI最新版本
知识大胖
NVIDIAGPU和大语言模型开发教程dockerllmopenwebui
实战需求OpenWebUI是一个可扩展、功能丰富且用户友好的自托管WebUI,旨在完全离线运行。它支持各种LLM运行器,包括Ollama和OpenAI兼容API。如何通过docker自动将其更新到OpenWebUI最新版本?系列文章《OpenWebUI系列之如何通过docker更新到OpenWebUI的最新版本》权重0,本地类、opewebui类《OpenWebUI系列之如何通过docker自动将
- STM32 CubMax 6.1.1 版本安装包
姜奇惟Sparkling
STM32CubMax6.1.1版本安装包【下载地址】STM32CubMax6.1.1版本安装包本仓库提供STM32CubeMX6.1.1版本的安装包,支持Linux、macOS和Windows64位系统。STM32CubeMX是STMicroelectronics推出的一款图形化配置工具,能够自动生成适用于STM32微控制器的初始化代码,极大地简化了开发流程。用户只需根据操作系统选择相应的安装包
- 使用STM32单片机控制步进电动机是一个常见的应用场景
QoyOle
单片机stm32mongodb
使用STM32单片机控制步进电动机是一个常见的应用场景。步进电动机可以通过产生脉冲信号来控制转动角度和速度。在本文中,我们将详细介绍如何使用STM32单片机来生成脉冲信号并控制步进电动机。下面是一个简要的步骤概览:初始化STM32单片机的GPIO引脚:首先,我们需要初始化单片机的GPIO引脚,以将其配置为输出模式。这些引脚将用于产生脉冲信号,并控制步进电动机的步进脚。具体的引脚配置取决于你使用的具
- C++中的智能指针
智能指针是C++中用于自动化管理动态内存的类模板,通过封装原生指针,并利用RAII(资源获取即初始化)技术,确保内存的自动释放,从而避免内存泄漏和悬空指针问题。它是现代C++内存管理的核心工具之一。原生指针的缺陷:1.内存泄漏:忘记调用delete2.悬空指针:释放后仍访问指针3.重复释放:同一内存被多次delete智能指针的优势:1.自动释放内存,不需手动delete,超出作用域自动释放2.防止
- 使用NVIDIA NeRF将2D图像转换为逼真的3D模型(Python)
ByteWhiz
3dpython计算机视觉Python
使用NVIDIANeRF将2D图像转换为逼真的3D模型(Python)NeuralRadianceFields(NeRF)是一种强大的方法,可以将2D图像转换为逼真的3D模型。它使用神经网络来建模场景的辐射场,并通过渲染多个视角的图像来重建3D模型。在本文中,我们将使用Python和NVIDIANeRF库来实现这一过程。首先,我们需要安装所需的库。我们可以通过以下命令使用pip安装NVIDIANe
- C++中的智能指针(1):unique_ptr
一、背景普通指针是指向某块内存区域地址的变量。如果一个指针指向的是一块动态分配的内存区域,那么即使这个指针变量离开了所在的作用域,这块内存区域也不会被自动销毁。动态分配的内存不进行释放则会导致内存泄漏。如果一个指针指向的是一块已经被释放的内存区域,那么这个指针就是悬空指针。使用悬空指针会造成不可预料的后果。如果我们定义了一个指针但未初始化使其指向有效的内存区域时,这个指针就成了野指针。使用野指针访
- linux/ubuntu启动引导过程详细分析
奇妙之二进制
#linuxubuntupostgresql
文章目录**一、固件初始化阶段(BIOS/UEFI)****1.BIOS(基本输入输出系统)模式****2.UEFI(统一可扩展固件接口)模式****二、引导加载程序阶段(GRUB2)****1.GRUB2的加载过程****2.GRUB配置解析****3.内核参数传递****三、内核加载与初始化****1.内核解压缩与启动****2.initramfs(初始内存文件系统)加载****3.根文件系统
- Spring 如何干预 Bean 的生命周期?
冰糖心书房
SpringIOCIocspringBean生命周期
Spring提供了多种机制让我们能够在Bean生命周期的不同节点“插入”自己的逻辑,这些机制可以分为两大类:针对单个Bean的干预和针对所有/多个Bean的全局干预。一、针对单个Bean的干预(最常用)这些方法让你为一个特定的Bean类定义其初始化和销毁逻辑。1.使用JSR-250注解(推荐方式)这是现在最优雅、也是Spring官方推荐的方式。它使用Java的标准注解,与Spring框架解耦。@P
- 【Modern C++ Part7】_创建对象时使用()和{}的区别
莫彩
ModernC++C++c++开发语言
在C++11中,你可以有多种语法选择用以对象的初始化,这样的语法显得混乱不堪并让人无所适从,(),=,{}均可以用来进行初始化:intx(0);//使用()进行初始化inty=0;//使用=进行初始化intz{0};//使用{}进行初始化在很多情况下,可以同时使用=和{}intz={0};//使用{}和=进行初始化对于这一条,我通常的会忽略“等于-{}”这种语法,因为C通常认为它只有{}。认为这种
- 运维笔记<4> xxl-job打通
GeminiJM
运维javaxxl-job
新的一天,来点新的运维业务,今天是xxl-job的打通其实在非集群中,xxl-job的使用相对是比较简单的,相信很多人都有使用的经验这次我们的业务场景是在k8s集群中,用xxl-job来做定时调度加上第一次倒腾,也是遇到了不少问题,在这里做一些记录1.xxl-job的集群安装首先是xxl-job的集群安装先贴上xxl-jobsql初始化文件的地址:xxl-job/doc/db/tables_xxl
- 深入解析TCP:可靠传输的核心机制与实现逻辑
Gappsong874
网络tcp/ip网络协议web安全网络安全大数据
TCP协议概述TCP(TransmissionControlProtocol)是一种面向连接的、可靠的传输层协议。它通过一系列机制确保数据准确、有序地从发送方传递到接收方,适用于对可靠性要求高的场景(如网页浏览、文件传输)。可靠传输的核心机制三次握手建立连接TCP通过三次握手(Three-WayHandshake)初始化连接,确保双方具备收发能力:SYN:客户端发送SYN=1和随机序列号seq=x
- linux orangepi串口5开发并且初始化
2301_78702511
linux运维服务器
因为串口5文件并没有配置,所以需要我们进行配置;#include//包含标准输入输出库#include//包含字符串处理函数库#include//包含错误号库#include//包含POSIX线程库#include//包含WiringPi库,用于GPIO控制#include//应该是包含WiringPi串口库的,但注意这个头文件可能不是标准WiringPi的一部分#include//包含标准库函数
- JQ+vue实现图片拼接(无限套娃版)
小周同学:
jsvuejqueryvue.jsjavascriptjquery
css样式/*css初始化*/*{margin:0;padding:0;}/*去掉li的小圆点*/li{list-style:none;}/*去掉a的下划线*/a{text-decoration:none;}/*搜索框去除边框*/input,button,select{border:0;/*设置背景颜色为透明*/background-color:transparent;/*去掉外轮廓*/outli
- NumPy-@运算符详解
GG不是gg
numpynumpy
NumPy-@运算符详解一、@运算符的起源与设计目标1.从数学到代码:符号的统一2.设计目标二、@运算符的核心语法与运算规则1.基础用法:二维矩阵乘法2.一维向量的矩阵语义3.高维数组:批次矩阵运算4.广播机制:灵活的形状匹配三、@运算符与其他乘法方式的核心区别1.对比`np.dot()`2.对比元素级乘法`*`3.对比`np.matrix`的`*`运算符四、典型应用场景:从基础到高阶1.深度学习
- LeetCode[位运算] - #137 Single Number II
Cwind
javaAlgorithmLeetCode题解位运算
原题链接:#137 Single Number II
要求:
给定一个整型数组,其中除了一个元素之外,每个元素都出现三次。找出这个元素
注意:算法的时间复杂度应为O(n),最好不使用额外的内存空间
难度:中等
分析:
与#136类似,都是考察位运算。不过出现两次的可以使用异或运算的特性 n XOR n = 0, n XOR 0 = n,即某一
- 《JavaScript语言精粹》笔记
aijuans
JavaScript
0、JavaScript的简单数据类型包括数字、字符创、布尔值(true/false)、null和undefined值,其它值都是对象。
1、JavaScript只有一个数字类型,它在内部被表示为64位的浮点数。没有分离出整数,所以1和1.0的值相同。
2、NaN是一个数值,表示一个不能产生正常结果的运算结果。NaN不等于任何值,包括它本身。可以用函数isNaN(number)检测NaN,但是
- 你应该更新的Java知识之常用程序库
Kai_Ge
java
在很多人眼中,Java 已经是一门垂垂老矣的语言,但并不妨碍 Java 世界依然在前进。如果你曾离开 Java,云游于其它世界,或是每日只在遗留代码中挣扎,或许是时候抬起头,看看老 Java 中的新东西。
Guava
Guava[gwɑ:və],一句话,只要你做Java项目,就应该用Guava(Github)。
guava 是 Google 出品的一套 Java 核心库,在我看来,它甚至应该
- HttpClient
120153216
httpclient
/**
* 可以传对象的请求转发,对象已流形式放入HTTP中
*/
public static Object doPost(Map<String,Object> parmMap,String url)
{
Object object = null;
HttpClient hc = new HttpClient();
String fullURL
- Django model字段类型清单
2002wmj
django
Django 通过 models 实现数据库的创建、修改、删除等操作,本文为模型中一般常用的类型的清单,便于查询和使用: AutoField:一个自动递增的整型字段,添加记录时它会自动增长。你通常不需要直接使用这个字段;如果你不指定主键的话,系统会自动添加一个主键字段到你的model。(参阅自动主键字段) BooleanField:布尔字段,管理工具里会自动将其描述为checkbox。 Cha
- 在SQLSERVER中查找消耗CPU最多的SQL
357029540
SQL Server
返回消耗CPU数目最多的10条语句
SELECT TOP 10
total_worker_time/execution_count AS avg_cpu_cost, plan_handle,
execution_count,
(SELECT SUBSTRING(text, statement_start_of
- Myeclipse项目无法部署,Undefined exploded archive location
7454103
eclipseMyEclipse
做个备忘!
错误信息为:
Undefined exploded archive location
原因:
在工程转移过程中,导致工程的配置文件出错;
解决方法:
- GMT时间格式转换
adminjun
GMT时间转换
普通的时间转换问题我这里就不再罗嗦了,我想大家应该都会那种低级的转换问题吧,现在我向大家总结一下如何转换GMT时间格式,这种格式的转换方法网上还不是很多,所以有必要总结一下,也算给有需要的朋友一个小小的帮助啦。
1、可以使用
SimpleDateFormat SimpleDateFormat
EEE-三位星期
d-天
MMM-月
yyyy-四位年
- Oracle数据库新装连接串问题
aijuans
oracle数据库
割接新装了数据库,客户端登陆无问题,apache/cgi-bin程序有问题,sqlnet.log日志如下:
Fatal NI connect error 12170.
VERSION INFORMATION: TNS for Linux: Version 10.2.0.4.0 - Product
- 回顾java数组复制
ayaoxinchao
java数组
在写这篇文章之前,也看了一些别人写的,基本上都是大同小异。文章是对java数组复制基础知识的回顾,算是作为学习笔记,供以后自己翻阅。首先,简单想一下这个问题:为什么要复制数组?我的个人理解:在我们在利用一个数组时,在每一次使用,我们都希望它的值是初始值。这时我们就要对数组进行复制,以达到原始数组值的安全性。java数组复制大致分为3种方式:①for循环方式 ②clone方式 ③arrayCopy方
- java web会话监听并使用spring注入
bewithme
Java Web
在java web应用中,当你想在建立会话或移除会话时,让系统做某些事情,比如说,统计在线用户,每当有用户登录时,或退出时,那么可以用下面这个监听器来监听。
import java.util.ArrayList;
import java.ut
- NoSQL数据库之Redis数据库管理(Redis的常用命令及高级应用)
bijian1013
redis数据库NoSQL
一 .Redis常用命令
Redis提供了丰富的命令对数据库和各种数据库类型进行操作,这些命令可以在Linux终端使用。
a.键值相关命令
b.服务器相关命令
1.键值相关命令
&
- java枚举序列化问题
bingyingao
java枚举序列化
对象在网络中传输离不开序列化和反序列化。而如果序列化的对象中有枚举值就要特别注意一些发布兼容问题:
1.加一个枚举值
新机器代码读分布式缓存中老对象,没有问题,不会抛异常。
老机器代码读分布式缓存中新对像,反序列化会中断,所以在所有机器发布完成之前要避免出现新对象,或者提前让老机器拥有新增枚举的jar。
2.删一个枚举值
新机器代码读分布式缓存中老对象,反序列
- 【Spark七十八】Spark Kyro序列化
bit1129
spark
当使用SparkContext的saveAsObjectFile方法将对象序列化到文件,以及通过objectFile方法将对象从文件反序列出来的时候,Spark默认使用Java的序列化以及反序列化机制,通常情况下,这种序列化机制是很低效的,Spark支持使用Kyro作为对象的序列化和反序列化机制,序列化的速度比java更快,但是使用Kyro时要注意,Kyro目前还是有些bug。
Spark
- Hybridizing OO and Functional Design
bookjovi
erlanghaskell
推荐博文:
Tell Above, and Ask Below - Hybridizing OO and Functional Design
文章中把OO和FP讲的深入透彻,里面把smalltalk和haskell作为典型的两种编程范式代表语言,此点本人极为同意,smalltalk可以说是最能体现OO设计的面向对象语言,smalltalk的作者Alan kay也是OO的最早先驱,
- Java-Collections Framework学习与总结-HashMap
BrokenDreams
Collections
开发中常常会用到这样一种数据结构,根据一个关键字,找到所需的信息。这个过程有点像查字典,拿到一个key,去字典表中查找对应的value。Java1.0版本提供了这样的类java.util.Dictionary(抽象类),基本上支持字典表的操作。后来引入了Map接口,更好的描述的这种数据结构。
&nb
- 读《研磨设计模式》-代码笔记-职责链模式-Chain Of Responsibility
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/**
* 业务逻辑:项目经理只能处理500以下的费用申请,部门经理是1000,总经理不设限。简单起见,只同意“Tom”的申请
* bylijinnan
*/
abstract class Handler {
/*
- Android中启动外部程序
cherishLC
android
1、启动外部程序
引用自:
http://blog.csdn.net/linxcool/article/details/7692374
//方法一
Intent intent=new Intent();
//包名 包名+类名(全路径)
intent.setClassName("com.linxcool", "com.linxcool.PlaneActi
- summary_keep_rate
coollyj
SUM
BEGIN
/*DECLARE minDate varchar(20) ;
DECLARE maxDate varchar(20) ;*/
DECLARE stkDate varchar(20) ;
DECLARE done int default -1;
/* 游标中 注册服务器地址 */
DE
- hadoop hdfs 添加数据目录出错
daizj
hadoophdfs扩容
由于原来配置的hadoop data目录快要用满了,故准备修改配置文件增加数据目录,以便扩容,但由于疏忽,把core-site.xml, hdfs-site.xml配置文件dfs.datanode.data.dir 配置项增加了配置目录,但未创建实际目录,重启datanode服务时,报如下错误:
2014-11-18 08:51:39,128 WARN org.apache.hadoop.h
- grep 目录级联查找
dongwei_6688
grep
在Mac或者Linux下使用grep进行文件内容查找时,如果给定的目标搜索路径是当前目录,那么它默认只搜索当前目录下的文件,而不会搜索其下面子目录中的文件内容,如果想级联搜索下级目录,需要使用一个“-r”参数:
grep -n -r "GET" .
上面的命令将会找出当前目录“.”及当前目录中所有下级目录
- yii 修改模块使用的布局文件
dcj3sjt126com
yiilayouts
方法一:yii模块默认使用系统当前的主题布局文件,如果在主配置文件中配置了主题比如: 'theme'=>'mythm', 那么yii的模块就使用 protected/themes/mythm/views/layouts 下的布局文件; 如果未配置主题,那么 yii的模块就使用 protected/views/layouts 下的布局文件, 总之默认不是使用自身目录 pr
- 设计模式之单例模式
come_for_dream
设计模式单例模式懒汉式饿汉式双重检验锁失败无序写入
今天该来的面试还没来,这个店估计不会来电话了,安静下来写写博客也不错,没事翻了翻小易哥的博客甚至与大牛们之间的差距,基础知识不扎实建起来的楼再高也只能是危楼罢了,陈下心回归基础把以前学过的东西总结一下。
*********************************
- 8、数组
豆豆咖啡
二维数组数组一维数组
一、概念
数组是同一种类型数据的集合。其实数组就是一个容器。
二、好处
可以自动给数组中的元素从0开始编号,方便操作这些元素
三、格式
//一维数组
1,元素类型[] 变量名 = new 元素类型[元素的个数]
int[] arr =
- Decode Ways
hcx2013
decode
A message containing letters from A-Z is being encoded to numbers using the following mapping:
'A' -> 1
'B' -> 2
...
'Z' -> 26
Given an encoded message containing digits, det
- Spring4.1新特性——异步调度和事件机制的异常处理
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- squid3(高命中率)缓存服务器配置
liyonghui160com
系统:centos 5.x
需要的软件:squid-3.0.STABLE25.tar.gz
1.下载squid
wget http://www.squid-cache.org/Versions/v3/3.0/squid-3.0.STABLE25.tar.gz
tar zxf squid-3.0.STABLE25.tar.gz &&
- 避免Java应用中NullPointerException的技巧和最佳实践
pda158
java
1) 从已知的String对象中调用equals()和equalsIgnoreCase()方法,而非未知对象。 总是从已知的非空String对象中调用equals()方法。因为equals()方法是对称的,调用a.equals(b)和调用b.equals(a)是完全相同的,这也是为什么程序员对于对象a和b这么不上心。如果调用者是空指针,这种调用可能导致一个空指针异常
Object unk
- 如何在Swift语言中创建http请求
shoothao
httpswift
概述:本文通过实例从同步和异步两种方式上回答了”如何在Swift语言中创建http请求“的问题。
如果你对Objective-C比较了解的话,对于如何创建http请求你一定驾轻就熟了,而新语言Swift与其相比只有语法上的区别。但是,对才接触到这个崭新平台的初学者来说,他们仍然想知道“如何在Swift语言中创建http请求?”。
在这里,我将作出一些建议来回答上述问题。常见的
- Spring事务的传播方式
uule
spring事务
传播方式:
新建事务
required
required_new - 挂起当前
非事务方式运行
supports
&nbs