【人工智能】传统机器学习算法（QDU）

转载请务必经过我的同意

• 【人工智能】不确定性推理（QDU）
• 【人工智能】传统机器学习算法（QDU）
• 【人工智能】非线性分类器（QDU）
• 【人工智能】机器学习基础（QDU）
• 【人工智能】深度学习（QDU）

线性分类器

涉及内容：

1. Fisher 线性判别
2. 感知器算法

分类器与准则

分类器的作用：

常规任务是利用给定的类别、已知的训练数据来学习分类规则和分类器，然后对未知数据进行分类（或预测）。逻辑回归（logistics）、SVM等常用于解决二分类问题，对于多分类问题（multi-class classification），比如识别手写数字，它需要10个分类，同样也可以用逻辑回归或SVM，只是需要多个二分类来组成多分类，但这样容易出错且效率不高，常用的多分类方法有softmax。

分类算法可以按不同的方式划分：

1. 基于概率密度的方法和基于判别函数的方法。
   • 基于概率密度的分类算法通常借助于贝叶斯理论体系，采用潜在的类条件概率密度函数的知识进行分类； 在基于概率密度的分类算法中，有著名的贝叶斯估计法、最大似然估计，这些算法属于有参估计，需要预先假设类别的分布模型，然后使用训练数据来调整概率密度中的各个参数。另外，如 Parzen窗、Kn邻近等方法属于无参估计，此类方法可从训练样本中直接估计出概率密度。 基于判别函数的分类方法使用训练数据估计分类边界完成分类，无需计算概率密度函数。
   • 基于判别函数的方法则假设分类规则是由某种形式的判别函数表示，而训练样本可用来表示计算函数中的参数，并利用该判别函数直接对测试数据进行分类。此类分类器中，有著名的Fisher准则、感知器方法、最小平方误差法、SVM法、神经网络方法以及径向基（RBF）方法等。
2. 根据监督方式划分分类算法，分类学习问题可分为三大类：有监督分类、半监督分类和无监督分类。
   • 有监督分类是指用来训练分类器的所有样本都经过了人工或其他方式的标注，有很多著名的分类器算法都属于有监督的学习方式，如AdaBoost[51]，SVM，神经网络算法以及感知器算法。
   • 无监督分类是指所有的样本均没有经过标注，分类算法需利用样本自身信息完成分类学习任务，这种方法通常被称为聚类，常用的聚类算法包括期望最大化（EM）算法和模糊C均值聚类算法等。
   • 半监督分类指仅有一部分训练样本具有类标号，分类算法需要同时利用有标号样本和无标号样本学习分类，使用两种样本训练的结果比仅使用有标注的样本训练的效果更好。这类算法通常由有监督学习算法改进而成，如SemiBoost、流形正则化、半监督SVM等。

---

线性（二）分类器的定义：线性分类器就是用一个“超平面”将正、负样本隔离开。

常见的线性分类器有：LR，贝叶斯分类，单层感知机、线性回归，SVM（线性核）等。

非线性分类器的定义：非线性分类器就是用一个“超曲面”或者多个超平（曲）面的组合将正、负样本隔离开（即，不属于线性的分类器）。

常见的非线性（二）分类器：决策树、RF、GBDT、多层感知机、SVM（高斯核）等。

准则：

以线性分类器为例，在基于判别函数的方法中，准则用于构建合适的判别函数，或者是为判别函数确定最佳参数。

线性判别准则中比较经典的是，FIsher准则、感知机准则、最小二乘（最小均方误差）准则。

注：在许多博客中不区分LDA（Linear Discriminant Analysis）与FDA（Fisher Discriminant Analysis），所以这部分就不细致区分了。只要理解线性判别分析中包含了哪些准则以及准则的内容即可。

下文中若未作特别说明，则不区分“FDA”、“LDA”、“Fisher线性判别分析”、“Fisher准则”之间的细致概念，即同义。

引入：K-邻近算法的局限性

K-Nearest Neighbor分类器（K-邻近算法）进行分类存在很多不足：

1. 分类器必须记住所有训练数据并将其存储起来，以便于未来测试数据用于比较。这在存储空间上是低效的，数据集很容易过大。
2. 对一个测试图像进行分类需要和所有训练图像作比较，算法计算资源耗费高。

因为K-邻近算法的这些不足，我们引入了线性分类器。

Fisher准则

要学习线性判别绝对不能一上来就学习其函数，要先从整体思路上掌握！

基本思想

FDA是一种监督学习的降维技术，以二维数据集的二分类为例（通俗点讲二维数据集就是平面直角坐标系中的散点，二分类就是这些数据集要么是第一类，要么是第二类），有很多种方法对这些点进行分类，比如我们可以找一条直线去分隔两类点，线左边的是第一类，线右边的是第二类等等方法。而线性判别要做的是找一条直线，让这些散点都投影到该直线上，让同一类的点尽可能在直线上分布地近点，而不同类的点在直线上分布尽可能地远点。

可能还是有点抽象，我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

上图提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的红色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。

在实际应用中，散点类别的确定往往不能仅由两种特征来确定，这就需要将FDA扩展到高维了。对于高维而言也是类似的，无非就是要去确定一个超平面，使得高维坐标系中的点投影到该超平面上同一类点尽可能近，不同类点尽可能远。降维就是FDA的主要思想。

判别函数

线性判别函数需要确定$W$和$w_0$可以用于判断某个样本$X$所在的类

判别函数：$g(X)=W^{T}X+w_0$

其中，$X$为样本的特征（即样本点在高维坐标系下的坐标）；$W$为权向量（即待求参数），$w_0$为阈值权，是个常数。

在二分类中，判别函数的意义在于确定一个决策面（决策面就是用于分隔每类散点的超平面），决策面的一侧为第一类点，另一侧为第二类点，在面上的点我们可以将该点归为第一类也可以归为第二类，也可以选择不对这些点分类。根据其意义，可以总结出判别规则：
$$\{\begin{array}{l}ifg(X)>0,thenX\in clas{s}_1\\ ifg(X)<0,thenX\in clas{s}_2\\ ifg(X)=0,thenX\in clas{s}_{1}orclas{s}_2\end{array}$$
那么，$g(X)=0$就是对应的决策面方程，即$W^{T}X+w_0=0$

准则函数

准则函数是用于获取最佳$W$的函数，通过下面的讲解会发现准则函数是用于确定投影方向的函数

以FDA“同近异远”的主要思想为目标定义Fisher准则函数，当准则函数的值尽可能地大（或者小）时可以使两类尽量分开，同类尽量聚集。也就是说我们要将分类的好坏程度量化，用于量化的函数就是Fisher准则函数（可以理解为损失函数），当其值取最大（或最小）时得到的参数值就是我们的目标参数值，也就是决策面。

---

获取投影方向$W$

以二分类为例。

将$X$空间中的$N$个具有$d$个特征（即$d$维）的样本点$x_1$，$x_2$，$...$，$x_N$通过一个$d$维向量$w$投影到一维$Y$空间中，其中$N_1$个属于$w_1$类的样本记为子集${\Gamma }_1$，$N_2$个属于$w_2$类的样本记为子集${\Gamma }_2$。投影到一维$Y$空间中，对应为$y_i=W^T{x}_i$，$i=1,2,...,N$。

基本参量：

在$d$维$X$空间中，

• 各类样本的均值向量$m_i$
  $$m_i=\frac{1}{N_i}\sum _{x\in {\Gamma }_i}x,i=1,2$$

• 样本类内离散度矩阵$S_i$
  $$S_i=\sum _{x\in {\Gamma }_i}(x-m_i)(x-m_i{)}^T,i=1,2$$

  $S_i$为对称阵

• 总样本类内离散度矩阵$S_w$
  $$S_w=S_1+S_2$$

• 样本类间离散度矩阵$S_b$
  $$S_b=(m_1-m_2)(m_1-m_2{)}^T$$

  $S_b$为对称阵

在一维$Y$空间中，

• 各类样本的均值$\widetilde{m_i}$
  $$\widetilde{m_i}=\frac{1}{N_i}\sum _{x_j\in {\Gamma }_i}{y}_j,i=1,2$$

  为了表示方便，$\widetilde{m_i}$式中的$x_j$和$y_j$将简写为$x$和$y$，含义不变，$y$为$x$对应的投影值

• 样本类内离散度$\widetilde{S_i^2}$
  $$\widetilde{S_i^2}=\sum x\in {\Gamma }_i(y-\widetilde{m_i}{)}^2,i=1,2$$

• 总样本类内离散度$\widetilde{S_w}$
  $$\widetilde{S_w}=\widetilde{S_1^2}+\widetilde{S_2^2}$$

• 总样本类间散度$\widetilde{S_b^2}$
  $$\widetilde{S_b^2}=(\widetilde{m_1}-\widetilde{m_2}{)}^2$$

Fisher准则函数定义为：
$$max{J}_F(W)=\frac{(\widetilde{m_1}-\widetilde{m_2}{)}^2}{\widetilde{S_1^2}+\widetilde{S_2^2}}$$

表示的含义即为“同近异远”

由各类样本的均值可推出：
$$\widetilde{m_i}=\frac{1}{N_i}\sum _{x\in {\Gamma }_i}y=\frac{1}{N_i}\sum _{x\in {\Gamma }_i}{W}^{T}x=W^T(\frac{1}{N_i}\sum _{x\in {\Gamma }_i}x)=W^T{m}_i$$
这样，Fisher准则函数$J_F(W)$的分子可写成：
$$\begin{gathered} (\widetilde{m_1}-\widetilde{m_2}{)}^2 \\ =(W^T{m}_1-W^T{m}_2{)}^2 \\ =(W^T{m}_1-W^T{m}_2)(W^T{m}_1-W^T{m}_2{)}^T \\ =W^T(m_1-m_2)(m_1-m_2{)}^{T}W \\ =W^T{S}_{b}W \end{gathered}$$
现在再来考察$J_F(w)$的分母与$W$的关系：
$$\begin{gathered} \widetilde{S_i^2}=\sum _{x\in {\Gamma }_i}(y-\widetilde{m_i}{)}^2 \\ =\sum _{x\in {\Gamma }_i}(W^{T}x-W^T{m}_i{)}^2 \\ =W^T[\sum _{x\in {\Gamma }_i}(x-m_i)(x-m_i{)}^T]W \\ {W}^T{S}_{w}W \end{gathered}$$
因此，
$$\widetilde{S_1^2}+\widetilde{S_2^2}=W^T(S_1+S_2)W=W^T{S}_{w}W$$
将上述各式代入$J_F(w)$，可得：
$$J_F(w)=\frac{W^T{S}_{b}W}{W^T{S}_{w}W}$$
最佳变换向量$W^{\ast }$的求取：

为求使$J_F(w)=\frac{W^T{S}_{b}W}{W^T{S}_{w}W}$取极大值时的$w^{\ast }$，可以采用Lagrange乘数法求解。令分母等于非零常数，即：
$$W^T{S}_{w}W=c\ne 0$$
定义Lagrange函数为：
$$L(W,\lambda )=W^T{S}_{b}W-\lambda (W^T{S}_{w}W-c)$$
其中$\lambda$为Lagrange乘子。将上式对$W$求偏导数，可得：
$$\frac{\partial L(W,\lambda )}{\partial w}=S_{b}W-\lambda S_{w}W$$
令偏导数为零，则有：
$$\begin{gathered} S_b{W}^{\ast }-\lambda S_w{W}^{\ast }=0 \\ {S}_b{W}^{\ast }=\lambda S_w{W}^{\ast } \end{gathered}$$
其中$W^{\ast }$就是$J_F(W)$的极值解。因为$S_w$非奇异，将上式两边左乘$S_W^{-1}$，可得：
$$S_w^{-1}{S}_b{W}^{\ast }=\lambda W^{\ast }$$
上式为求一般矩阵$S_w^{-1}{S}_b$的特征值问题。利用$S_b=(m_1-m_2)(m_1-m_2{)}^T$的定义，将上式左边的$S_b{W}^{\ast }$写成：
$$S_b{W}^{\ast }=(m_1-m_2)(m_1-m_2{)}^T{W}^{\ast }=(m_1-m_2)R$$
其中$R=(m_1-m_2{)}^T{W}^{\ast }$为标量，所以$S_b{W}^{\ast }$总在向量$(m_1-m_2)$的方向上。因此$\lambda W^{\ast }$可写成：
$$\lambda W^{\ast }=S_w^{-1}(S_b{W}^{\ast })=S_w^{-1}(m_1-m_2)R$$
从而可得：
$$W^{\ast }=\frac{R}{\lambda }{S}_w^{-1}(m_1-m_2)$$
由于我们的目的是寻找最佳的投影方向，$W^{\ast }$的比例因子对此并无影响，因此可忽略比例因子$\frac{R}{\lambda }$，有：
$$W^{\ast }=S_w^{-1}(m_1-m_2)$$
$W^{\ast }$是使Fisher准则函数$J_F(W)$取极大值时的解，也就是$d$维$X$空间到一维$Y$空间的最佳投影方向。

获取阈值$w_0$

有了$W^{\ast }$，就可以把$d$维样本$x$投影到一维，这实际上是多维空间到一维空间的一种映射，这个一维空间的方向$W^{\ast }$相对于Fisher准则函数$J_F(W)$是最好的。利用Fisher准则确定$W$后，就可以将$d$维分类问题转化为一维分类问题，然后，只要确定一个阈值$w_0$即可。

阈值$w_0$的选取：

1. $d$和$N$很大时，$y$近似正态分布，可在Y空间内用贝叶斯分类器

2. 经验，如：

   $w_0=-\frac{1}{2}(\widetilde{m_1}+\widetilde{m_2})$

   $w_0=-\tilde{m}$

   $w_0=-\frac{1}{2}(\widetilde{m_1}+\widetilde{m_2})-\frac{1}{N_1+N_2-2}ln\frac{P(w_1)}{P(w_2)}$

3. 在实际工作中还可以对$w_0$进行逐次修正的方式，选择不同的$w_0$值，计算其对训练样本集的错误率，找到错误率较小的$w_0$值

感知器算法

基本思想

对于线性判别函数，当模式的维数已知时，判别函数的形式实际上就已经确定下来，线性判别的过程即是确定权向量。感知器是一种神经网络模型，其特点是随意确定判别函数初始值，在对样本分类训练过程中，针对分类错误的样本不断进行权值修正，逐步迭代直至最终分类符合预定标准，从而确定权向量值。可以证明感知器是一种收敛算法，只要模式类别是线性可分的，就可以在有限的迭代步数里求出权向量的解。

判别函数

设样本$d$维特征空间中描述，则两类别问题中线性决策面的一般形式可表示成：$g(X)=W^{T}X+w_0$

将线性判别函数齐次化为：$g(X)=W^{T}X+w_0={\alpha }^{T}y$

其中，$y=\left[\begin{array}{c}x\\ 1\end{array}\right]$称为增广样本向量，$\alpha =\left[\begin{array}{c}w\\ w_0\end{array}\right]$称为增广权向量。

线性判别函数的齐次简化使特征空间增加了一维，但保持了样本间的欧氏距离不变， 对于分类效果也与原决策面相同，只是在Y空间中决策面是通过坐标原点的。

判别规则（与Fisher中类似）：
$$g(X)={\alpha }^{T}y\{\begin{array}{l}ifg(X)>0,thenX\in clas{s}_1\\ ifg(X)<0,thenX\in clas{s}_2\\ ifg(X)=0,thenX\in clas{s}_{1}orclas{s}_2\end{array}$$

反过来说，如果存在一个权向量$\alpha$，使得对于任何$y\in clas{s}_1$都有${\alpha }^T>0$， 而对任何$y<clas{s}_2$，都有${\alpha }^{T}y<0$， 则称这组样本集为线性可分的，否则称样本集为线性不可分的。

准则函数

样本的规范化

根据线性可分的定义，如果样本集$y_1,y_2,...,y_N$是线性可分的，则必存在某个或某些权向量$\alpha$，使得
$$g(X)={\alpha }^{T}y\{\begin{array}{l}>0,对于一切X\in clas{s}_1\\ <0,对于一切X\in clas{s}_2\end{array}$$
如果将第二类样本都取其反向向量，则有：
$$y^{\prime }=\{\begin{array}{l}y,ify\in clas{s}_1\\ -y,ify\in clas{s}_2\end{array}$$
也就是说不管样本原来的类别标识，只要找到一个对全部样本都满足${\alpha }^T{y}_i^{\prime }>0,i=1,2,..,N$的权向量$\alpha$即可。

注：为了方便，下文中使用$y$表示上文中的$y^{\prime }$

感知器准则函数

本质是用对所有错分样本的求和来表示对错分样本的惩罚。

如果样本$y_k$被错分，则有${\alpha }^T{y}_k<0$，因此可定义如下的感知准则函数：
$$J_P(\alpha )=\sum _{y_j\in {\gamma }^k}(-{\alpha }^T{y}_j)$$
其中，${\gamma }^k$是被$\alpha$错分样本的集合。当且仅当$J_P({\alpha }^{\ast })=min{J}_P(\alpha )=0$时，无错分样本。

感知器准则函数求解

梯度下降法（非单样本修正法）：
$$\alpha (k+1)=\alpha (k)-{\rho }_k\nabla J$$
其中，$\alpha (k)$表示第$k$次迭代，${\rho }_k$为步长。表示下一时刻的权向量是把当前时刻的权向量向目标函数的负梯度方向调整一个修正量。

其中，
$$\nabla J=\partial J_P(\alpha )/\partial \alpha =\sum _{y_j\in {\gamma }^k}(-y_j)$$
因此，
$$\alpha (k+1)=\alpha (k)+{\rho }_k\sum _{y_j\in {\gamma }^k}(-y_j)$$
表示每一步迭代时把错分的样本按照某个系数加到权向量上。

单样本修正法：

不难看出，梯度下降法（非单样本修正法）每次迭代必须遍历全部样本点，才能得到$\alpha (k)$下的错分样本集${\gamma }^k$，这是十分低效的，更 常用是每次只修正一个样本或一批样本的固定增量法。

单样本修正法把样本集看做一个不断重复出现的序列而逐个加以考虑。对于任意权向量$\alpha (k)$，如果把某个样本分错了， 则对$\alpha (k)$做一次修正。

单样本修正法的修正过程：

• 固定增量法

  （1）初值$\alpha (0)$任意

  （2）对样本$y_j$，若$\alpha (k{)}^T{y}_j<0$，则$\alpha (k+1)=\alpha (k)+{\rho }_k{y}_j$，其中${\rho }_k$一般取$1$

  （3）对所有样本重复（2），直至$J_P=0$

• 变增量法

  ${\rho }_k$会变化。

  例如绝对修正法：${\rho }_k=\frac{|\alpha (k{)}^T{y}_j|}{||y_j|{|}^2}$

  不进行细致讲解。

收敛：对线性可分样本集，经过有限次修正后一定可以找到一个解${\alpha }^{\ast }$

计算题

题目

已知有两类样本

​ $w_1=(x_1,x_2)=\{(1,0,1{)}^T,(0,1,1{)}^T\}$

​ $w_2=(x_3,x_4)=\{(1,1,0{)}^T,(0,1,0{)}^T\}$

假设初始权向量 $a_1=(1,1,1,1{)}^T$ ，${\rho }_k=1$

试用感知准则函数法求判别函数？

解答

• 对样本进行变换，变成增广向量。

  $x_1=(1,0,1,1{)}^T$

  $x_2=(0,1,1,1{)}^T$

  $x_3=(1,1,0,1{)}^T$

  $x_4=(0,1,0,1{)}^T$

• 对样本进行规范化。

  $x_1=(1,0,1,1{)}^T$

  $x_2=(0,1,1,1{)}^T$

  $x_3=-(1,1,0,1{)}^T$

  $x_4=-(0,1,0,1{)}^T$

• 初始权向量 $a_1=(1,1,1,1{)}^T$ ，${\rho }_k=1$

1. 第一次迭代：

   $a_1^T{x}_1=(1,1,1,1)(1,0,1,1{)}^T=3>0$

   $\therefore$ 不修正，$a_2=a_1=(1,1,1,1{)}^T$

   $a_2^T{x}_2=(1,1,1,1)(0,1,1,1{)}^T=3>0$

   $\therefore$ 不修正，$a_3=a_2=(1,1,1,1{)}^T$

   $a_3^T{x}_3=-(1,1,1,1)(1,1,0,1{)}^T=-3<0$

   $\therefore$ 修正，$a_4=a_3+{\rho }_k{x}_3=(0,0,1,0{)}^T$

   $a_4^T{x}_4=-(0,0,1,0)(0,1,0,1{)}^T=0$

   $\therefore$ 修正，$a_5=a_4+{\rho }_k{x}_4=(0,-1,1,-1{)}^T$

   经过第一轮迭代发现权向量有修改，需要进行第二轮迭代。

2. 第二次迭代：

   $a_5^T{x}_1=(0,-1,1,-1)(1,0,1,1{)}^T=0$

   $\therefore$ 修正，$a_6=a_5+{\rho }_k{x}_1=(1,-1,2,0{)}^T$

   $a_6^T{x}_2=(1,-1,2,0)(0,1,1,1{)}^T=1>0$

   $\therefore$ 不修正，$a_7=a_6=(1,-1,2,0{)}^T$

   $a_7^T{x}_3=-(1,-1,2,0)(1,1,0,1{)}^T=0$

   $\therefore$ 修正，$a_8=a_7+{\rho }_k{x}_3=(0,-2,2,-1{)}^T$

   $a_8^T{x}_4=-(0,-2,2,-1)(0,1,0,1{)}^T=0$

   $\therefore$ 不修正，$a_9=a_8=(0,-2,2,-1{)}^T$

   经过第二轮迭代发现权向量有修改，需要进行第三轮迭代。

3. 第三次迭代：

   $a_9^T{x}_1=(0,-2,2,-1)(1,0,1,1{)}^T=1>0$

   $\therefore$ 不修正，$a_{10}=a_9=(0,-2,2,-1{)}^T$

   $a_{10}^T{x}_2=(0,-2,2,-1)(0,1,1,1{)}^T=-1<0$

   $\therefore$ 修正，$a_{11}=a_{10}+{\rho }_k{x}_2=(0,-1,3,0{)}^T$

   $a_{11}^T{x}_3=-(0,-1,3,0)(1,1,0,1{)}^T=1>0$

   $\therefore$ 不修正，$a_{12}=a_{11}=(0,-1,3,0{)}^T$

   $a_{12}^T{x}_4=-(0,-1,3,0)(0,1,0,1{)}^T=1>0$

   $\therefore$ 不修正，$a_{13}=a_{12}=(0,-1,3,0{)}^T$

   经过第三轮迭代发现权向量有修改，需要进行第四轮迭代。

4. 第四次迭代：

   $a_{13}^T{x}_1=(0,-1,3,0)(1,0,1,1{)}^T=3>0$

   $\therefore$ 不修正，$a_{14}=a_{13}=(0,-1,3,0{)}^T$

   $a_{14}^T{x}_2=(0,-1,3,0)(0,1,1,1{)}^T=2>0$

   $\therefore$ 不修正，$a_{15}=a_{14}=(0,-1,3,0{)}^T$

   $a_{15}^T{x}_3=-(0,-1,3,0)(1,1,0,1{)}^T=1>0$

   $\therefore$ 不修正，$a_{16}=a_{15}=(0,-1,3,0{)}^T$

   $a_{16}^T{x}_4=-(0,-1,3,0)(0,1,0,1{)}^T=1>0$

   $\therefore$ 不修正，$a_{17}=a_{16}=(0,-1,3,0{)}^T$

   经过第四轮迭代发现权向量没有修改，迭代结束。

因此，最终权向量$a=a_{17}=(0,-1,3,0{)}^T$，判别函数为$g(X)=a^{T}X=-x_2+3x_3$

多类问题

对于多类问题，模式有$w_1$，$w_2$，$...$，$w_m$个类别。可分三种情况：

1. 绝对可分（一对多，one-vs-rest, one-over-all）
2. 成对可分
3. 最大值判决（直接多类分类）

第一种情况：绝对可分

每一模式类与其它模式类间可用单个判别平面把一个类分开，$c$类转化为$c$个两类问题，$w_i$与非$w_i$

简单来说，就是先将$w_1$的样本作为一组，$w_2$，$...$，$w_m$的样本作为另一组，根据这两组画一条线将两组分隔；再将$w_2$的样本作为一组，$w_1$，$w_3$，$...$，$w_m$的样本作为另一组根据这两组再画一条线将两组分隔，以此类推。

缺点：

1. 训练样本不均衡而导致分类面有偏（假设多类中各类的训练样本数相当）
2. 出现歧义区域，不会恰好得到c个区域（往往过多）

通过下图观察更加直观：

如果$X$属于$w_1$，则由图可清楚看出，这时$g_1(x)>0$而$g_2(x)<0$，$g_3(x)<0$。 $w_1$类与其它类之间的边界由$g_1(x)=0$确定。

例题： 已知三类$w_1$，$w_2$，$w_3$的判别函数分别为：
$$\{\begin{array}{l}{g}_1(x)=-x_1+x_2\\ g_2(x)=x_1+x_2-5\\ g_3(x)=-x_2+1\end{array}\stackrel{三个判别边界为：}{}\{\begin{array}{l}{g}_1(x)=-x_1+x_2=0\\ g_2(x)=x_1+x_2-5=0\\ g_3(x)=-x_2+1=0\end{array}$$

如果某个$X$使二个以上的判别函数 $g_i(x)>0$，则$X$就无法作出确切的判决。 如图中$IR1$，$IR3$，$IR4$区域。另一种情况是$IR2$区域，判别函数都为负值。$IR1$，$IR2$，$IR3$，$IR4$都为不确定区域。

第二种情况：成对可分

对多类中的每两类构造一个分类器，所以每个模式类和其它模式类间可分别用判别平面分开，因此对于$c$类就有$\frac{c(c-1)}{2}$个决策面。

相较于“一对多”，决策歧义区域相对较小。

判别函数：$g_{ij}(x)=W_{ij}^{T}x$

判别边界：$g_{ij}(x)=0$

判别条件：$g_{ij}(x)\{\begin{array}{l}>0,当x\in w_1\\ <0,当x\in w_2\end{array}i\ne j$

判别函数性质：$g_{ij}(x)=g_{ji}(x)$

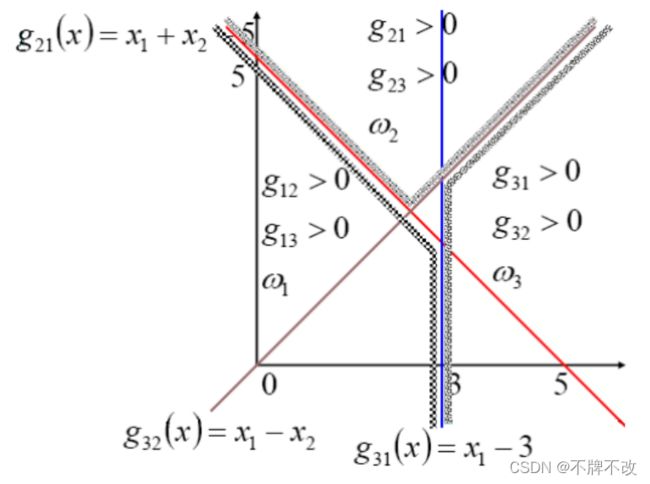
还是通过样例来说明：

假设判别函数为：$\{\begin{array}{l}{g}_{12}(x)=-x_1-x_2+5\\ g_{13}(x)=-x_1+5\\ g_{23}(x)=-x_1+x_2\end{array}$

例题： 未知模式$X=(x_1,x_2{)}^T=(4,3{)}^T$属于上面的哪一类？

代入判别函数可得：$g_{12}(x)=-2$，$g_{13}(x)=-1$，$g_{23}(x)=-1$

把下标对换可得：$g_{21}(x)=2$，$g_{31}(x)=1$，$g_{32}(x)=1$

因为$g_{3j}(x)>0$，所以$X$属于$w_3$类

第三种情况：最大值判决

每类都有一个判别函数。

判别函数：$g_k(x)=W_{k}Xk=1,2,...,M$

判别规则：$$g_i(x)=W_K^{T}X\{\begin{array}{l}最大,当x\in w_i\\ 小,其他\end{array}$$

判别边界：$g_i(x)=g_j(x)$或$g_i(x)-g_j(x)=0$

就是说，要判别模式$X$属于哪一类，先把$X$代入$M$个判别函数中，判别函数最大的那个类别就是$X$所属类别。

此分类实现方式也称作多类线性机器

多类线性机器不会出现有决策歧义的区域。下图显示三类的情况：

利用感知准则实现多类判别

步骤：

（1）增广样本，但是不用进行规范化（注意和两分类问题的区别）

（2）每一类设定一个初始权向量

（3）对第$i$类的样本$y_i$，若$w_i^T{y}_i<=w_t^T{y}_i$，$t=1,...,M,t\ne i$，则
$$\{\begin{array}{ll}{w}_i(k+1)=w_i(k)+y_i& \\ w_t(k+1)=w_t(k)-y_i& t\ne i\end{array}$$

（4）对所有样本重复（3），直到满足$w_i^T{y}_i>w_t^T{y}_i$，$t=1,..,M$，$t\ne i$

注意，当存在修改时，只对不满足条件的$t$对应的权向量进行修改，并非只要不满足（4）就要对全部权向量进行修改！

例题：

有三类样本$w_1:\{(0,0{)}^T\}$，$w_2:\{(1,1{)}^t\}$，$w_3:\{(-1,1{)}^T\}$，采用感知器算法设计判别函数。

解答：

（2）对样本进行变换，变换成增广向量。

$x_1=(0,0,1{)}^T$

$x_2=(1,1,1{)}^T$

$x_3=(-1,1,1{)}^T$

（2）初始权向量为$w(1)=w(2)=w(3)=(0,0,0{)}^T$，并令$c=1$

此时对于所有样本，全向量不再修改，迭代停止

$w_1=w_1(8)=(0,-2,0{)}^T$

$w_2=w_2(8)=(2,0,-2{)}^T$

$w_3=w_3(8)=(-2,0,-2{)}^T$

判别函数：

$g_1(x)=-2x_2$

$g_2(x)=2x_1-2$

$g_3(x)=-2x_1-2$

REF

线性判别分析LDA原理总结 - 博客园

线性判别分析（LDA）准则：FIsher准则、感知机准则、最小二乘（最小均方误差）准则 - 博客园

机器学习总结之——线性分类器与非线性分类器 - CSDN

分类器 - CSDN

10 模式识别- 感知器分类方法（单样本修正法+非单样本修正法）- CSDN