【学习10】CNN、validation set、Spatial Transformer Layer
深度学习框架CNN
一张图片是一个三维的tensor(维度大于2的矩阵),分别是图片的宽高和channel。一张图片都是由RGB三原色组成的,所以三个channel就代表了三原色,长宽代表图片的解析度(代表图片的像素pixel)。每一个one-hot vector的一个数值就代表了某个位置某种颜色的强度。
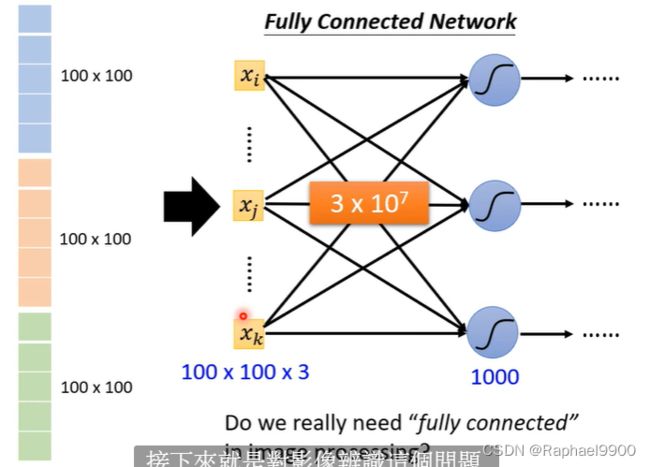
参数越多,越有可能产生overfit。在一张图片里面,我们需要把一个一维的矩阵向量作为输入,在fully connected network(每条连线都有weight)里面就可能会发生overfit。
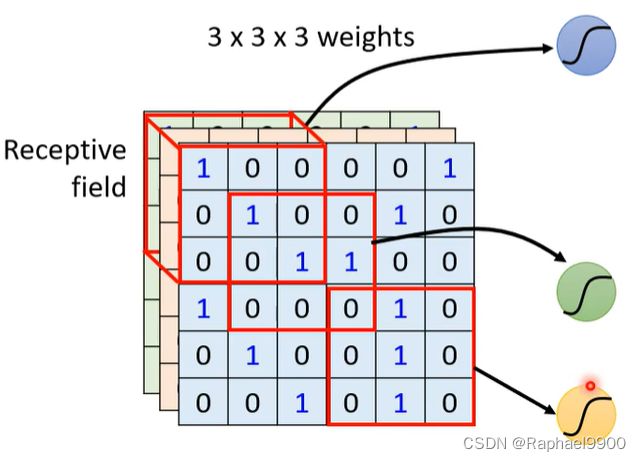
在我们日常观察中,我们只是根据特征来判别一张图片,而对于机器而言也是如此,可能不需要整张图片的所有信息。在CNN里面,每个neuron都只关心自己的receptive field里面的内容。receptive field是可以重叠的,也可以是同一个。
receptive field一般默认是三个channel都会截取,这里用kernel size来描述它的宽高。在图像识别的时候一般取3*3的kernel size。当划分了 receptive field之后,往往会有一组neuron守备。
我们希望两个receptive field是有重叠的,不重叠的地方宽stride(移动stride之后再取receptive field)。当receptive field到了边缘的时候,我们就会在多出的地方补0(或者补receptive field,或者补平均)。
虽然receptive field里可能有很多的neuron来守备,但是这样会多了很多输入。所以我们想在neuron里面能不能共享参数,w值一样,输入不一样。这里的前提是receptive field的位置不一样,可以有重叠。同一个receptive field的参数不能一样。
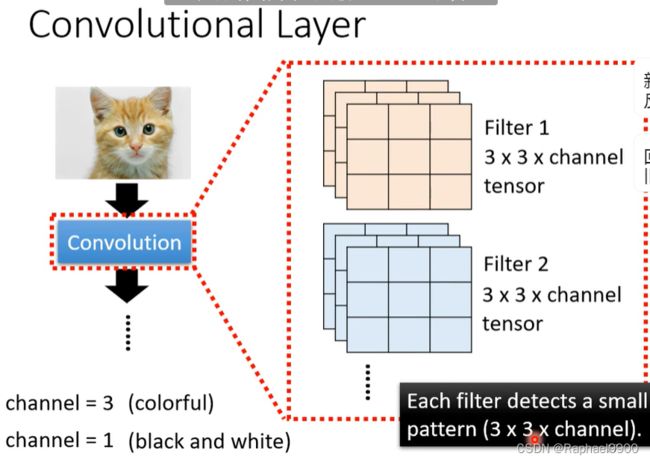
Convolutional Layer
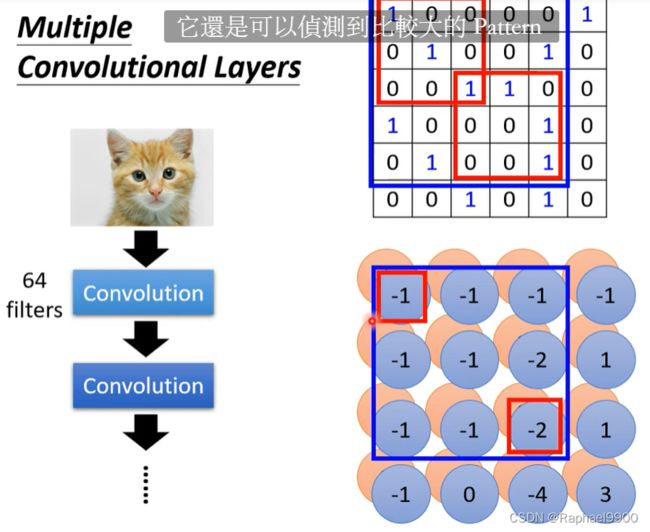
假设我们的参数已经找到了(参数要通过gradient descend寻找),这里是就组成了一个个filter。对每一个参数矩阵(filter 3*3*3)和原来的图片进行相乘之后,我们得到了一个4*4*64(这里因为有64个filter,所以channel是64)的矩阵。
在这里我们设置filter的大小为3*3*64。
在max pooling里面,我们需要选择每个filter形成的矩阵的最大的那个为代表值。上面的图片进行pooling之后会把图片变小,而对于外观来说基本没有什么影响。
今天也有人不选pool,因为有运算变快了。
Flatten
做完convolution和max pooling之后,就是FLatten和Fully connected Feedforward network的部分
Flatten的意思是,把左边的feature map拉直,然后把它丢进一个Fully connected Feedforward network,然后就结束了,也就是说,我们之前通过CNN提取出了image的feature,它相较于原先一整个image的vetor,少了很大一部分内容,因此需要的参数也大幅度地减少了,但最终,也还是要丢到一个Fully connected的network中去做最后的分类工作。
可以用一般的神经网络来做影像处理,不一定要用CNN。比如说,你想要做图像的分类,那你就去训练一个neural network,它的输入是一张图片,你就用里面的像素pixel来表示这张图片。也就是一个很长很长的向量,而输出则是由图像类别组成的向量。假设你有1000个类别,那输出就有1000个维度。但是,我们现在会遇到的问题是这样子:实际上,在训练神经网络的时候,我们会有一种期待说,在这个网络结构里面的每一个神经元,都应该代表了一个最基本的分类器。
为什么需要用验证集validation set
在有监督(supervise)的机器学习中,数据集常被分成2~3个即:
训练集(train set) 验证集(validation set) 测试集(test set)
一般需要将样本分成独立的三部分训练集(train set),验证集(validation set)和测试集(test set)。其中训练集用来估计模型,验证集用来确定网络结构或者控制模型复杂程度的参数,而测试集则检验最终选择最优的模型的性能如何。一个典型的划分是训练集占总样本的50%,而其它各占25%,三部分都是从样本中随机抽取。
样本少的时候,上面的划分就不合适了。常用的是留少部分做测试集。然后对其余N个样本采用K折交叉验证法。就是将样本打乱,然后均匀分成K份,轮流选择其中K-1份训练,剩余的一份做验证,计算预测误差平方和,最后把K次的预测误差平方和再做平均作为选择最优模型结构的依据。特别的K取N,就是留一法(leave one out)。
training set是用来训练模型或确定模型参数的,如ANN中权值等; validation set是用来做模型选择(model selection),即做模型的最终优化及确定的,如ANN的结构;而 test set则纯粹是为了测试已经训练好的模型的推广能力。当然,test set这并不能保证模型的正确性,他只是说相似的数据用此模型会得出相似的结果。但实际应用中,一般只将数据集分成两类,即training set 和test set,大多数文章并不涉及validation set。
train
训练数据。拟合模型,用这部分数据来建立模型。
是一些我们已经知道输入和输出的数据集训练机器去学习,通过拟合去寻找模型的初始参数。例如在神经网络(Neural Networks)中, 我们用训练数据集和反向传播算法(Backpropagation)去每个神经元找到最优的比重(Weights)。
validation
验证数据。train建了一个模型,但是模型的效果仅体现了训练数据,但不一定适合同类的其他数据,所以建模前数据分成两部分,一部分为训练数据,一部分为验证数据(两部分数据的比例大致为7:3,这取决于你验证的方法)。另外,你也可能训练多个模型,但不知哪个模型性能更佳,这时可以将验证数据输入不同模型进行比较。
是一些我们已经知道输入和输出的数据集,通过让机器学习去优化调整模型的参数,在神经网络中, 我们用验证数据集去寻找最优的网络深度(number of hidden layers),或者决定反向传播算法的停止点;在普通的机器学习中常用的交叉验证(Cross Validation) 就是把训练数据集本身再细分成不同的验证数据集去训练模型。
test
测试数据。跟前两者的最大区别在于:train和validation数据均是同一对象的数据,但是测试,我们就需要用跨对象的数据来验证模型的稳定性。
用户测试模型表现的数据集,根据误差(一般为预测输出与实际输出的不同)来判断一个模型的好坏。
为什么验证数据集和测试数据集两者都需要?
因为验证数据集(Validation Set)用来调整模型参数从而选择最优模型,模型本身已经同时知道了输入和输出,所以从验证数据集上得出的误差(Error)会有偏差(Bias)。
但是我们只用测试数据集(Test Set) 去评估模型的表现,并不会去调整优化模型。
在传统的机器学习中,这三者一般的比例为training/validation/test = 50/25/25, 但是有些时候如果模型不需要很多调整只要拟合就可时,或者training本身就是training+validation (比如cross validation)时,也可以training/test =7/3.
但是在深度学习中,由于数据量本身很大,而且训练神经网络需要的数据很多,可以把更多的数据分给training,而相应减少validation和test。
为什么不直接使用两个数据集:一个训练集和一个测试集?直接在训练集上面训练模型,在测试集上面评估模型,这样不是更简单一些吗?
不这样做的原因在于,开发一个模型通常需要我们去调整模型的配置:例如,选择最佳的全连接层数或者每一层的节点数(这些被称之为模型的超参数,以区分于模型自身的参数,如:模型的权重和偏置)。我们通过模型在验证集上面的表现来做这种调整。本质上,这种调整也是一种学习的过程:在某种参数空间中寻找最佳的模型配置。结果,根据模型在验证集上面的表现来调整其配置会很快地导致模型在验证集上面过拟合,即便模型从来没有直接在验证集上进行训练。
产生这一现象的原因即所谓的“信息泄漏“。每一次基于模型在验证集上面的表现来调整某个超参数的时候,某些关于验证集的信息就会泄漏给模型。如果我们仅仅作一次这样的调整,那么只会有很少的信息被泄漏,那么你的验证集依然可以被用来评估模型。然而,如果你多次重复这一过程——运行一个实验,在验证集上面评估模型,然后修改模型——那么关于验证集的越来越多的信息会被泄漏个模型。
最后,我们只会得到一个在验证集上面表现良好的模型,因为你就是朝着这个方向去优化它的。然后我们所关心的是模型在新数据上面的表现,而不是验证集,所以我们需要应用一个完全不同的,全新的数据集来评价这个模型,即测试集。我们的模型不能够直接地或者间接地接触过任何关于测试集的信息。如果模型基于测试集的表现来进行调整的话,那么对模型的泛化能力的评价是存在缺陷的。
将现有数划分为训练集、验证集和测试集看起来是很直接的做法,然而这边还有一些高级的方式在数据有限的情况下来完成这种划分,包括:hold-out validation、k-fold validation和iterated k-fold validation with shuffling。
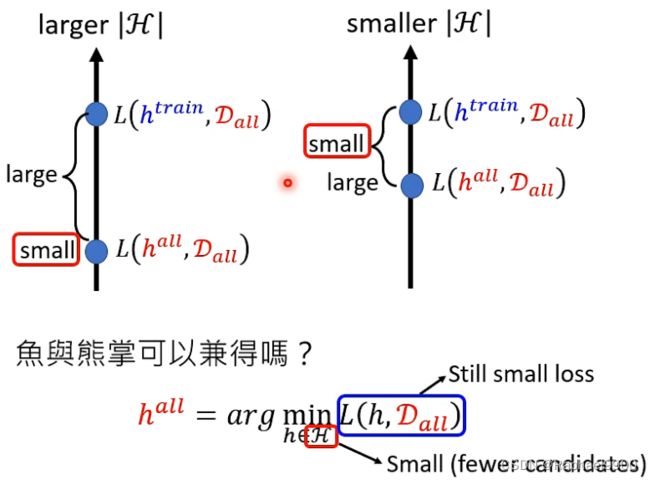
在上次的学习中,出现了这个问题。当H比较大的时候,我们的最佳L虽然是最小的,但是在训练的时候L就会与最小的L有很大的差距。当我们的H比较小的时候,我们的最佳L会比较大,但是这时候我们的训练L会与最佳L差距较小。而我们想要在H比较小的时候,能够得到很小的L。如何能实现呢?深度学习。
复习
如何用折线逼近一个曲线呢?我们找到每一个转折点,然后收尾相连,得到一条折线(piecewise linear)。而每一个piecewise linear都能由一个常数和很多组方形折线组成。
而每一个方形折线(又叫hard sigmoid)又能用sigmoid曲线近似
回到我们的一层neuron 网络里面
而如何表示上面的hard sigmoid方程呢?这里我们用到两个rectified linear unit(ReLU)方程来组合。
所以我们可以把上面的一层神经网络用relu来表示:
为什么深度学习模型要往深度做?如下是进行的一些数据上的对比,可以看出来,在深度上的错误率会比在广度上的错误率低的。
深度学习会更加的有效,不容易产生overfit。
产生同一个方程 ,深度学习模型需要的资料更少,层数越低。
空间变换层Spatial Transformer Layer
CNN对于缩放和旋转不是不变的,它会认为移动和缩放会不一样。如果能够识别更大的图,那可能是因为训练的时候有大图。
如果我们在a22那个值那边用四舍五入的方法计算的时候,我们就会发现这个位置没有变化,就不能用gradient descent。这里我们用了另一种方法来计算a22,这时候就能用gradient descent 了