一、语音识别方法(2)
一、语音识别方法(2)
1 声学模型
1.1 隐马尔可夫模型(HMM)
在此之前,首先需要明确马尔可夫链:
在随机过程中, t n t_n tn 时刻的状态 x n x_n xn 的条件分布,仅与其前一状态 x n − 1 x_{n-1} xn−1 有关,即:
P ( x n ∣ x 1 , x 2 , x 3 , . . . , x n − 1 ) = P ( x n ∣ x n − 1 ) P(x_n|x_1,x_2,x_3,...,x_{n-1}) = P(x_n|x_{n-1}) P(xn∣x1,x2,x3,...,xn−1)=P(xn∣xn−1)
(今天是否下雨仅与前一天是否下雨有关),将此称为马尔可夫过程。
隐马尔可夫模型本质上是对马尔可夫链的拓展,在过去直观信息不可见时(前一天是否下雨),通过过去其他已知信息(前一天的气温、湿度)去推导未知知识(今天是否下雨)。
在语音识别任务中,在不知道之前频谱具体意思的情况下,根据过去语音频谱去推导新频谱的对应结果。
因此在语音识别这类不定长映射关系中,面对不同长度的语音( x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3)和文本序列( w 1 , w 2 w_1, w_2 w1,w2),可采用隐马尔可夫链的形式进行表示:、
P ( X ∣ W ) = P ( x 1 , x 2 , x 3 ∣ w 1 , w 2 ) P(X|W) = P(x_1,x_2,x_3|w_1,w_2) P(X∣W)=P(x1,x2,x3∣w1,w2)
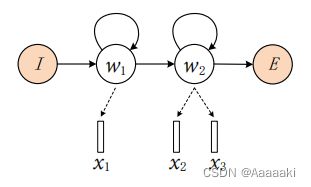
这种不受彼此约束的HMM隐含状态 w w w 和观测值 x x x ,解决了语音和文本序列不等长的问题。
根据隐马尔可夫链公式推导:
在声学模型中,其关键点在于计算 P ( X ∣ W ) P(X|W) P(X∣W) ,其中包括隐含状态 w w w 和观测值 x x x,根据隐马尔可夫的两条假设:
齐次马尔可夫性假设:即任意时刻的状态只依赖于前一时刻的状态,与其它时刻的状态及观测无关,存在公式
P ( W t ∣ W t − 1 , X t − 1 , . . . , W 1 , X 1 ) = P ( W t ∣ W t − 1 ) P(W_t|W_{t-1},X_{t-1},...,W_1,X_1)=P(W_t|W_{t-1}) P(Wt∣Wt−1,Xt−1,...,W1,X1)=P(Wt∣Wt−1)观测独立性假设:即任意时刻的观测仅依赖于此刻状态,与其它无关,存在公式:
P ( X t ∣ W t , X t − 1 , . . . , W 1 , X 1 ) = P ( X t ∣ W t ) P(X_t|W_t,X_{t-1},...,W_1,X_1) = P(X_t|W_t) P(Xt∣Wt,Xt−1,...,W1,X1)=P(Xt∣Wt)因此上述在基于隐马尔可夫的图结构中,所有变量的联合概率分布为:
P ( X ∣ W ) = P ( w 1 ) P ( x 1 ∣ w 1 ) ∏ i = 2 n P ( w i ∣ w i − 1 ) P ( x i ∣ w i ) = P ( w 1 ) P ( x 1 ∣ w 1 ) P ( w 2 ∣ w 1 ) P ( x 2 ∣ w 2 ) P ( w 2 ∣ w 2 ) P ( x 3 ∣ w 2 ) \begin{aligned} P(X|W) &= P(w_1)P(x_1|w_1) \prod_{i=2}^nP(w_i|w_{i-1})P(x_i|w_i) \\ &= P(w_1)P(x_1|w_1)P(w_2|w_1)P(x_2|w_2)P(w_2|w_2)P(x_3|w_2) \end{aligned} P(X∣W)=P(w1)P(x1∣w1)i=2∏nP(wi∣wi−1)P(xi∣wi)=P(w1)P(x1∣w1)P(w2∣w1)P(x2∣w2)P(w2∣w2)P(x3∣w2)
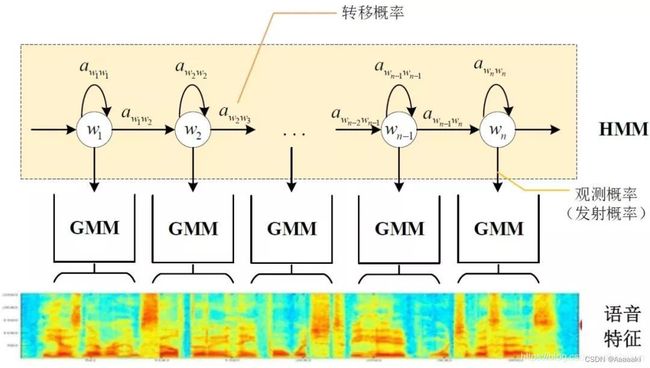
因此,隐马尔可夫模型可由三要素决定:初始状态概率、状态转移概率以及观测概率。
其中 P ( w 1 ) P(w_1) P(w1) 为初始时刻状态为 w 1 w_1 w1 的状态概率**(初始状态概率), P ( w 2 ∣ w 1 ) 、 P ( w 2 ∣ w 2 ) P(w_2|w_1)、P(w_2|w_2) P(w2∣w1)、P(w2∣w2) 为由 t − 1 t-1 t−1时刻转移到 t t t时刻且下一状态为 w 2 w_2 w2的概率(状态转移概率)**,二者均可基于常规统计方法从样本中计算出来。
但关键点在于隐马尔可夫模型的发射概率(观测概率)——在时刻 t t t处于状态 w i w_i wi,生成观测值 x i x_i xi的概率,即 P ( x 1 ∣ w 1 ) 、 P ( x 2 ∣ w 2 ) 、 P ( x 3 ∣ w 2 ) P(x_1|w_1)、P(x_2|w_2)、P(x_3|w_2) P(x1∣w1)、P(x2∣w2)、P(x3∣w2),这部分可通过混合高斯模型GMM或深度神经网络DNN进行求解。
传统语音识别系统普遍采用基于GMM-HMM的声学模型,具体示意图如下:
但这种方式只能学到语音的浅层特征,无法获取到数据特征间的高阶相关性,因此后续研究人员利用深度神经网络的强学习性,取代了GMM模型,进一步提高了识别性能。
1.2 高斯混合模型(GMM)
首先明确高斯模型:
对于一维数据样本,高斯分布遵循:
P ( x ∣ θ ) = 1 2 π σ 2 e x p ( − ( x − μ ) 2 2 σ 2 ) P(x|\theta)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(x-\mu)^2}{2\sigma^2}) P(x∣θ)=2πσ21exp(−2σ2(x−μ)2)
而当面对多维数据样本时,高斯分布则遵循:
P ( x ∣ θ ) = 1 ( 2 π ) D 2 ∣ Σ ∣ 1 2 e x p ( − ( x − μ ) T ∑ − 1 ( x − μ ) 2 ) P(x|\theta)=\frac{1}{(2\pi)^{\frac{D}{2}}\lvert \Sigma \rvert^{\frac{1}{2}}}exp(-\frac{(x-\mu)^T\sum^{-1}(x-\mu)}{2}) P(x∣θ)=(2π)2D∣Σ∣211exp(−2(x−μ)T∑−1(x−μ))
其中, μ \mu μ为期望, Σ \Sigma Σ 为协方差, D D D 为数据维度。
混合高斯模型则是由 K K K 个单高斯模型组合而成, K K K 个子模型作为混合模型的隐变量存在。通过给定合适的子高斯数 K K K ,理论上高斯混合模型可以实现任何概率分布的拟合。其概率分布为:
P ( x ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) P(x)=\sum^K_{k=1}\pi_kN(x|\mu_k,\Sigma_k) P(x)=k=1∑KπkN(x∣μk,Σk)
其中 N ( x ∣ μ k , Σ k ) N(x|\mu_k,\Sigma_k) N(x∣μk,Σk) 为混合模型中的第 K K K个分量,也可以理解为波峰数。 π k \pi_k πk 表示第 k k k个分量的权重,即 ∑ k = 1 K π k = 1 \sum^K_{k=1}\pi_k=1 ∑k=1Kπk=1,且 0 ≤ π k ≤ 1 0 \leq \pi_k \leq 1 0≤πk≤1。 μ k 、 Σ k \mu_k、\Sigma_k μk、Σk为每个高斯密度函数自己的期望和方差。
GMM可以描述多峰分布的数据,当 K = 3 K=3 K=3时,概率密度函数示例图像如下图所示:
因此GMM的本质是一个生成模型,它假设数据是从多个高斯分布中生成的,可以这样理解生成流程:有 K K K 个高斯分布,赋予每一个分布一个权重,每当生成一个数据时,就按权重的比例随机选择一个分布,然后按照该分布生成数据。
在语音识别任务中,由于HMM将文本中字词的粒度进行了分解,针对每个音素(Phone)考虑其上下文音素,如 /l-d-sil/,将其记为一个三音素(Triphone)。并采用一个独立的三状态HMM进行建模,从而实现将文本的基本单位由音素降解为微小的HMM状态。
但是考虑到不少三音素在语料中并未出现或数量极少,而且由于决策树的存在,三音素状态可以共享。因此对于共享 N N N个音素的句子,其最终保留的三音素状态个数要远小于 3 N 3 3N^3 3N3,记为 Senones。需要注意的是,这里的Senones是借助数学模型定义出来的音素变种,并不存在实际的听觉感受。
通过上述方式,每个语音帧和每个Senone间的对应关系表示为三音素HMM的发射概率 P ( x i ∣ s j ) P(x_i|s_j) P(xi∣sj),其中 s j s_j sj代表第 j j j 个Senone,与之对应的帧 x i x_i xi,其跨度常取为 25 m s 25ms 25ms,帧间步移为 10 m s 10ms 10ms。
Phone、Triphone和Senone的关系如下图所示:
GMM由于可拟合任意概率分布,因此常作为首选的发射概率模型。采用每个GMM对应一个Senone,并通过其各自的概率密度函数进行表示,单个三音素GMM-HMM结构如下图所示。
GMM模型在建模发射概率时,将每个帧看做空间中的独立单位,忽略了语音信号中的时序关系,因此采用帧内各维度相关性更小的MFCC特征更有利于GMM建模。
训练好GMM模型后,由于语音识别属于对连续变量进行建模,而连续变量间的概率比较可以等价的采用概率密度函数进行替代,因此通过对每个GMM模型的概率密度函数进行对比,即可求出发射概率 P ( x i ∣ s j ) P(x_i|s_j) P(xi∣sj),然后结合HMM的初始状态概率、状态转移概率。即可计算得到需要求的 P ( X ∣ W ) P(X|W) P(X∣W)。
GMM-HMM模型中,GMM的作用主要负责将提取到的MFCC特征映射为HMM的发射概率,提交给HMM进行 P ( X ∣ W ) P(X|W) P(X∣W) 的计算。
1.3 深度神经网络(DNN)
在GMM模型中,求取发射概率 P ( x i ∣ s j ) = P ( s i ∣ x j ) P ( x j ) P ( s j ) P(x_i|s_j)=\frac{P(s_i|x_j)P(x_j)}{P(s_j)} P(xi∣sj)=P(sj)P(si∣xj)P(xj) ,其中 P ( x j ) P(x_j) P(xj) 作为待解码语音的概率,属于固定值忽略不计,而先验概率 P ( s j ) P(s_j) P(sj) 属于Senone的出现概率,可通过统计学的方式计算获得。因此求 P ( x i ∣ s j ) P(x_i|s_j) P(xi∣sj)的过程可进一步归结为求取 P ( s i ∣ x j ) P(s_i|x_j) P(si∣xj)的过程,即Senone属于某段语音序列的概率,可看作是一个分类问题。
此时模型所求结果由似然概率 P ( x i ∣ s j ) P(x_i|s_j) P(xi∣sj)转化为了后验概率 P ( s i ∣ x j ) P(s_i|x_j) P(si∣xj)。
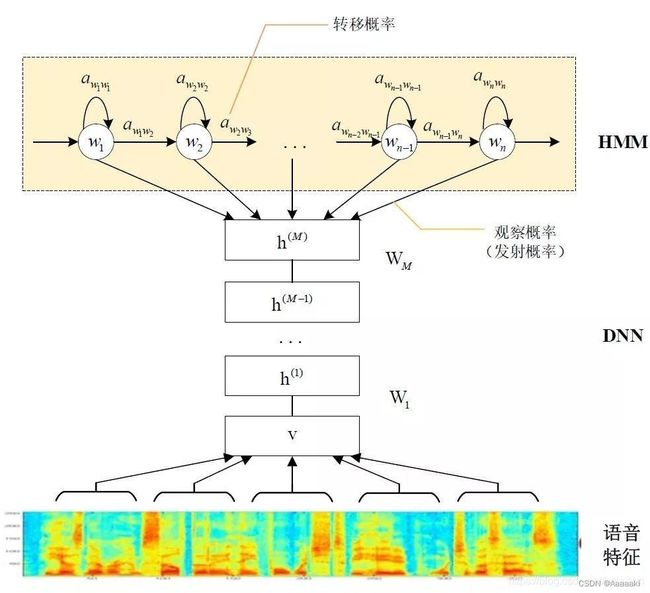
DNN的分类属于有监督学习,标签依赖性强。而在训练集中,只存在整条语音和整条文本的对应关系,因此需要GMM先捕捉数据中的内在关系,为DNN的数据集打好标签,再由DNN依靠其强大的学习能力和泛化能力进行未知数据的分类。整体结构如下图所示:
将提取到的语音特征输入到DNN中,由DNN引入先验概率 P ( s j ) P(s_j) P(sj),替代GMM进行语音特征映射,将其输出结果输入到HMM中进行HMM发射概率的计算,最终计算出 P ( X ∣ W ) P(X|W) P(X∣W)。
相较于GMM中对时序信息的忽略,DNN中通过引进循环神经网络(RNN),解决了这一问题,引入了对时序信息的考虑。
2 语言模型(LM)
不同于声学模型,语言模型在语音识别任务中,主要负责计算 P ( W ) P(W) P(W)的值,经典方法是采用n-gram语法或RNN模型进行求解。
2.1 n-gram模型
n-gram属于经典的自回归模型,对于给定的词序列 W = [ w 1 , w 2 , w 3 , . . . , w m ] W=[w_1,w_2,w_3,...,w_m] W=[w1,w2,w3,...,wm],在该模型中其概率表示为:
P ( W ) = P ( w 1 , w 2 , . . . , w m ) = ∏ i = 1 m P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) ∝ ∏ i = 1 m P ( w i ∣ w i − n + 1 , w i − n + 2 , . . . , w i − 1 ) \begin{aligned} P(W)&=P(w_1,w_2,...,w_m) \\ &=\prod_{i=1}^m P(w_i|w_1,w_2,...,w_{i-1}) \\ &\propto \prod_{i=1}^m P(w_i|w_{i-n+1},w_{i-n+2},...,w_{i-1}) \end{aligned} P(W)=P(w1,w2,...,wm)=i=1∏mP(wi∣w1,w2,...,wi−1)∝i=1∏mP(wi∣wi−n+1,wi−n+2,...,wi−1)
即在该模型中,当前词的出现概率仅与该词的前n个词有关,进而计算语料中对应词串出现的比列:
P ( w i ∣ w i − n + 1 , w i − n + 2 , . . . , w i − 1 ) = c o u n t ( w i ∣ w i − n + 1 , w i − n + 2 , . . . , w i ) c o u n t ( w i ∣ w i − n + 1 , w i − n + 2 , . . . , w i − 1 ) P(w_i|w_{i-n+1},w_{i-n+2},...,w_{i-1})=\frac{count(w_i|w_{i-n+1},w_{i-n+2},...,w_{i})}{count(w_i|w_{i-n+1},w_{i-n+2},...,w_{i-1})} P(wi∣wi−n+1,wi−n+2,...,wi−1)=count(wi∣wi−n+1,wi−n+2,...,wi−1)count(wi∣wi−n+1,wi−n+2,...,wi)
同时为避免因部分词串出现次数太少导致不平滑的现象,通过不同的smooth平滑算法进行处理。
2.2 RNN模型
对于单向循环神经网络RNN,其可天然用于句子序列建模,利用句中历史词来预测当前词。
在该结构中,每个节点输出产生该节点词的概率,即 P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) P(w_i|w_1,w_2,...,w_{i-1}) P(wi∣w1,w2,...,wi−1),从而直接求得 P ( W ) P(W) P(W)结果。
与n-gram相比,二者各有千秋。其中RNN可通过参数共享处理任意长度的历史信息,同时参数量更小,而n-gram每增加一次n的数量,参数量也会随之呈指数递增。但是n-gram胜在可编辑,其直接存储可见的各自词汇组合的可能性,RNN则是无法修改参数,进而增加新词。而且RNN中需要每次临时计算 P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) P(w_i|w_1,w_2,...,w_{i-1}) P(wi∣w1,w2,...,wi−1)的值,实时性要弱于预先存好 P ( w i ∣ w i − n + 1 , w i − n + 2 , . . . , w i − 1 ) P(w_i|w_{i-n+1},w_{i-n+2},...,w_{i-1}) P(wi∣wi−n+1,wi−n+2,...,wi−1)值的n-gram模型,因此在相同性能下,n-gram存储大小更大,但解码时间快于RNN。