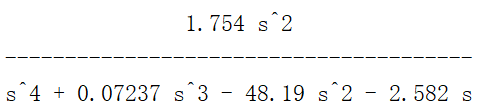倒立摆的模糊控制实验（基于matlab&simulink仿真）

倒立摆模糊控制仿真系统设计

实验目的：理解和掌握模糊控制系统的构成和设计方法，为实际工程应用打下基础。
基本要求：掌握以误差及其变化率为输入的典型模糊控制器的设计方法，了解影响模糊控制器性能的关键参数及调节方法。针对被控对象，构建合适的模糊控制器，搭建模糊控制系统。
实验内容提要：针对典型的二阶以上被控对象，设计模糊控制器。包括控制器输入输出量的选择，输入输出论域的模糊划分，模糊规则库的建立等。利用设计完成的模糊控制在Simulink中搭建模糊控制系统，要求该系统稳定且具有良好的动态及稳态特性。
实验工作概述：主要针对倒立摆进行了建模与模糊控制仿真，其中实验1-1是仅针对角度的模糊PID控制，实验1-2是针对位置与角度的分段模糊控制。后面也尝试进行了二级倒立摆的模糊控制设计，但由于知识水平不够没能完全实现，仅实现了第一级的直立控制。

实验1 单级倒立摆的PID模糊控制

一、被动对象数学描述与特性分析

关于倒立摆的相关背景：倒立摆，Inverted Pendulum ，是典型的多变量、高阶次、非线性、强耦合、自然不稳定系统。倒立摆系统的稳定控制是控制理论中的典型问题，在倒立摆的控制过程中能有效反映控制理论中的许多关键问题 ，如非线性问题、鲁棒性问题、随动问题、镇定、跟踪问题等。因此倒立摆系统作为控制理论教学与科研中典型的物理模型 ，常被用来检验新的控制理论和算法的正确性及其在实际应用中的有效性。所以我此次实验采用一阶倒立摆来验证。
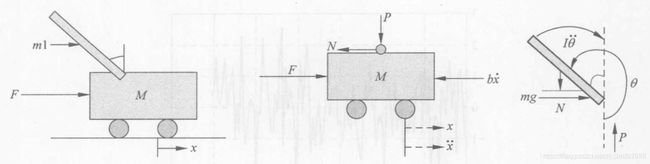当摆杆夹角很小时，近似线性化处理：

$(I+m{l}^2)\ddot{\theta }+mgl\theta =ml\ddot{x}$
$(M+m)\ddot{x}+b\dot{x}-ml\ddot{\theta }=u$

根据微分方程组做拉普拉斯变换联立求得外力针对角度的传递函数：

$\frac{\varphi (s)}{U(s)}=\frac{\frac{m{l}^2}{q}{s}^2}{s^4+\frac{b(I+m{l}^2)}{q}{s}^3-\frac{(M+m)mgl}{q}{s}^2-\frac{bmql}{q}s}$

将各种参数输入matlab，
编辑一个函数脚本GetPendulum来求传递函数的系数：

function [G] = GetPendulum(M,m,l)
b = 0.15;I = 0.005;
g = 9.81;
q = (M+m)*(I+m*l^2)-(m*l)^2;
num = [m*l/q 0 0];
den = [1 b*(I+m*l^2)/q (-(M+m)*m*g*l)/q (-b*m*g*l)/q 0];
G=tf(num,den);
end

当M=2，m=0.8，l=0.25时，求得：

这是一个典型的二阶系统

二、模糊控制器的设计步骤与具体参数选择

模糊集合设计：

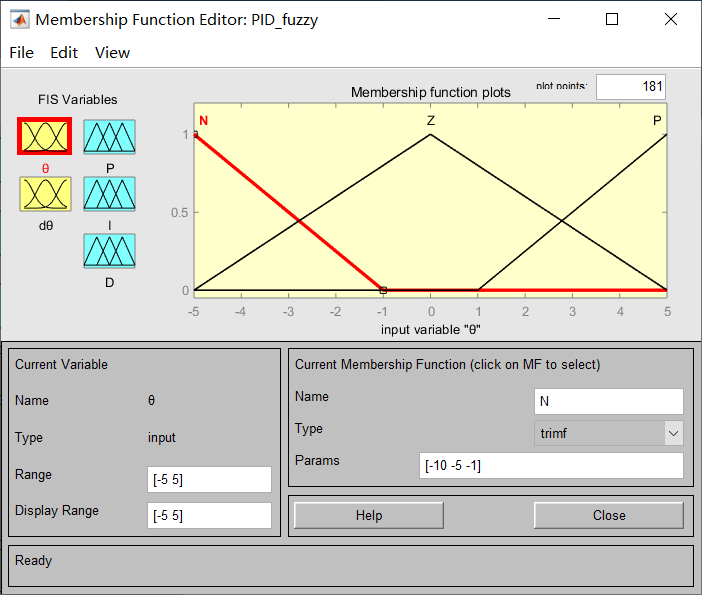
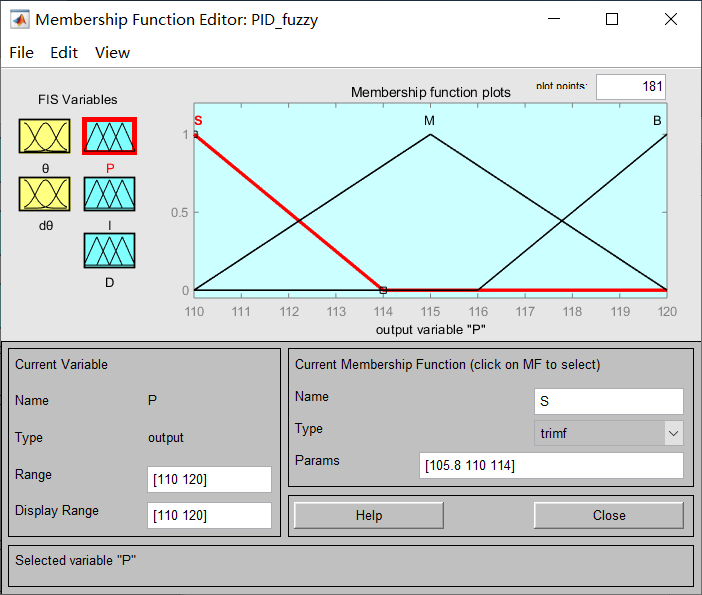
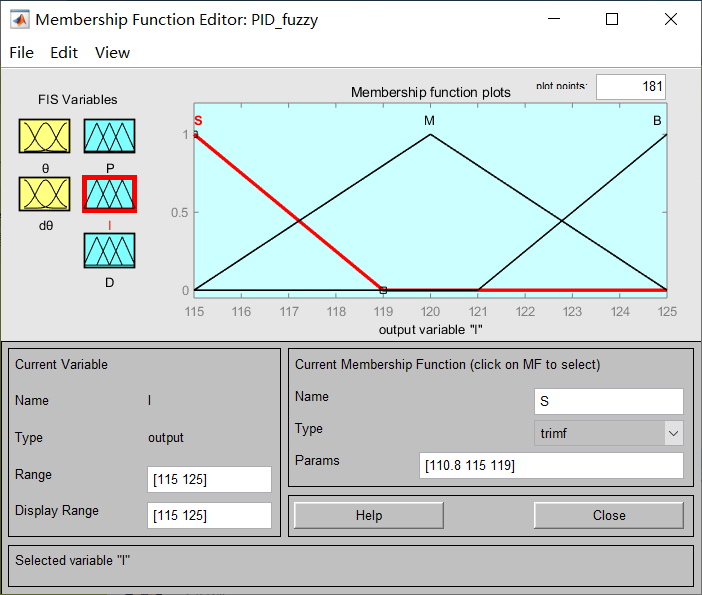
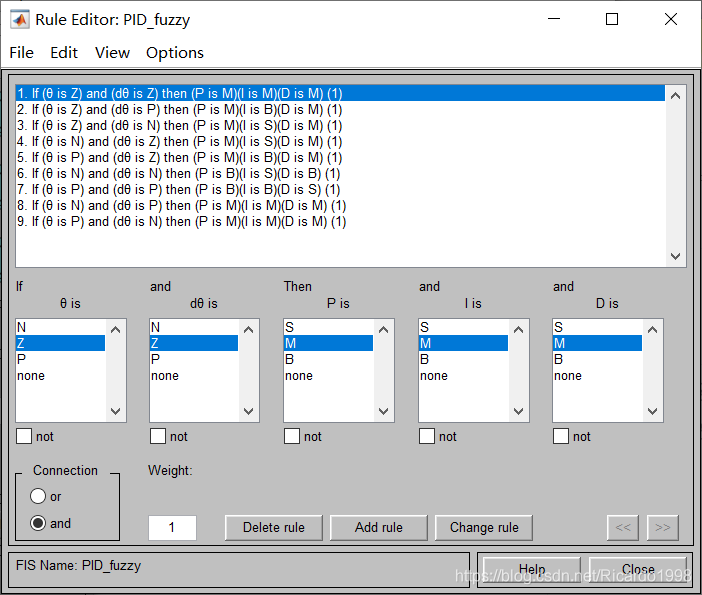
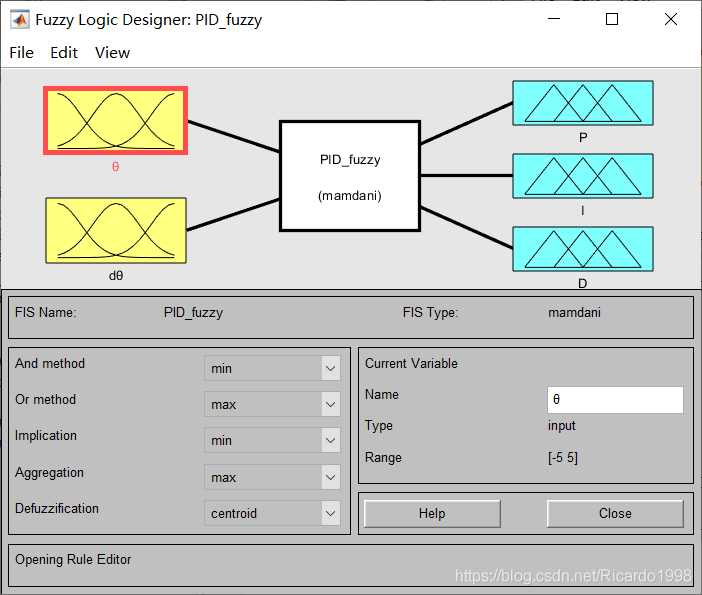
总共有两个输入三个输出，输入角度和角度微分的模糊集合划分都相同，论域为[-5,5]，模糊集合为3个，分别命名为：[N Z P]，输出P I D三个参数的范围分别为[110，120]，[115，125]，[80，90]，模糊集合为3个命名为：[S M B]它们的分布如上图所示。

模糊规则库的设计：

整个模糊控制器如下：

三、控制系统仿真程序的设计步骤与运行结果

在simulink中搭建简单的反馈控制模型，其中两个并行系统的控制任务分别由模糊PID控制器和普通PID控制器担任。普通PID控制器的三个控制参数分别选为：P:115 I:120 D:85。

输入分别选择阶跃信号和随机信号，对比输出结果：

阶跃信号输出结果

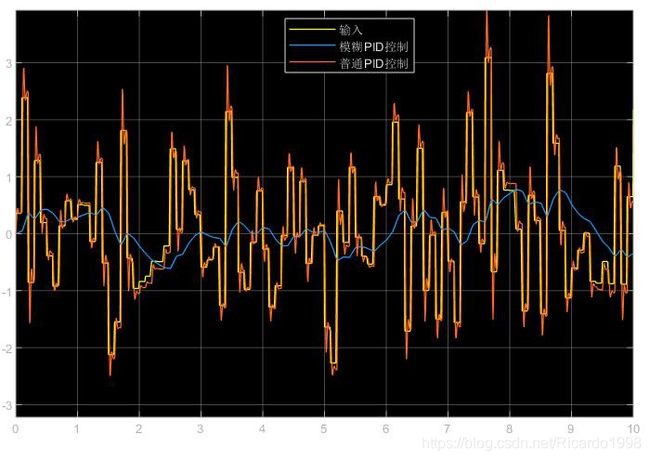
随机信号输出结果

四、总结与结论

可以看出，对于阶跃输入，虽然普通PID控制器响应较快，但是模糊PID控制效果相比更加平滑。而对于随机信号输入，普通PID的输出已经几乎跟随输入信号，失去了控制效果，而模糊PID控制器可以较好地克服随机信号的干扰，输出比较平滑且稳定。
当然，这只是将非线性的倒立摆系统简单地在平衡点附近近似为线性系统，所以对于非线性的倒立摆系统来说，当角度比较大时便不再适用，而且输入仅为角度，无法做到对于位置的控制，甚至有可能超出运动范围。这种设计在实际应用中可能并不合理，所以下面我设计了倒立摆的分段模糊控制系统。

实验2 单级倒立摆的分段模糊控制

一、被动对象数学描述与特性分析

重新建立单级倒立摆的精确微分方程模型
单级倒立摆示意图如下：
各种参数含义与取值：

符号	物理意义	单位与大小
$M$	小车质量	2kg
$m$	小球质量	0.8kg
$l$	摆杆长度	0.25m
$b_x$	小车摩擦系数	0.005kg/s
$b_{\theta }$	摆杆摩擦系数	0.0005$kg{m}^2/s$
$F$	小车受力（控制力）	-N
$x,x_2$	小车和小球位移	-m
$\theta$	摆杆摆角	-rad

建模过程：
由于现代控制理论中状态空间的相关内容还没有学完，我在这里只建立最朴素的微分方程模型，代入simulink直接求值。
根据拉格朗日方程，我们可以列出倒立摆的运动关系：

$L=T-V=1/2M{v}_1^2-mgcos\theta$

在上式中：

$v_1^2={\dot{x}}^2$

$v_2^2=(\frac{\mathrm{d}}{\mathrm{d}t}(x-lsin\theta ){)}^2+(\frac{\mathrm{d}}{\mathrm{d}t}(lcos\theta ){)}^2={\dot{x}}^2-2l\dot{x}\dot{\theta }cos\theta +l^2{\dot{\theta }}^2$

将$v_1^2$和$v_2^2$代入$L$中得：

$L=1/2(M+m){\dot{x}}^2=ml\dot{x}\dot{\theta }cos\theta +1/2m{l}^2{\dot{\theta }}^2=mgcos\theta$

此时列拉普拉斯方程：

$\frac{\mathrm{d}}{\mathrm{d}t}(\frac{\mathrm{d}L}{\mathrm{d}\dot{x}})-\frac{\mathrm{d}L}{\mathrm{d}x}=F-b_x\dot{x}$

$\frac{\mathrm{d}}{\mathrm{d}t}(\frac{\mathrm{d}L}{\mathrm{d}\dot{\theta }})-\frac{\mathrm{d}L}{\mathrm{d}\theta }=b_{\theta }\dot{\theta }$

在上式中代入$L$得：

$(M+m)\ddot{x}-ml\ddot{\theta }cos\theta +ml{\dot{\theta }}^{2}sin\theta =F-b_x\dot{x}$

$-\ddot{x}cos\theta +l\ddot{\theta }-gsin\theta =-b_{\theta }\dot{\theta }$

解出对应的$\ddot{\theta }$和$\ddot{x}$：

$\ddot{\theta }=1/(\frac{(M+m)}{cos\theta }l=mlcos\theta )[(M+m)gtan\theta =\frac{(M+m)}{cos\theta }{b}_{\theta }\dot{\theta }-ml{\dot{\theta }}^{2}sin\theta +F-b_x\dot{x}]$

$\ddot{x}=\frac{1}{M+m=mco{s}^2\theta }(mgsin\theta cos\theta -m{b}_{\theta }\dot{\theta }cos\theta -ml{\dot{\theta }}^{2}sin\theta +F-b_x\dot{x})$

此时利用状态空间方程的一点知识，构建状态变量：

$[x_1{x}_2{x}_3{x}_4{]}^T=[x\dot{x}\theta \dot{\theta }{]}^T$

列出四个状态变量的表达式：

${\dot{x}}_1=x_2$

${\dot{x}}_2=\frac{1}{M+m-mco{s}^2{x}_3}(mgsin{x}_{3}cos{x}_3-m{b}_{\theta }{x}_{4}cos{x}_3-ml{x}_4^{2}sin{x}_3+F-b_x{x}_2)$

${\dot{x}}_3=x_4$

${\dot{x}}_4=\frac{1}{\frac{(M+m)}{cos{x}_3}l-mlcos{x}_3}[(M+m)gtan{x}_3-\frac{(M+m)}{cos{x}_3}{b}_{\theta }{x}_4-m{x}_4^{2}sin{x}_3+F-b_x{x}_2]$

它们就是我们得出的微分方程模型。

二、模糊控制器的设计步骤与具体参数选择

初步设计：

模糊集合设计：

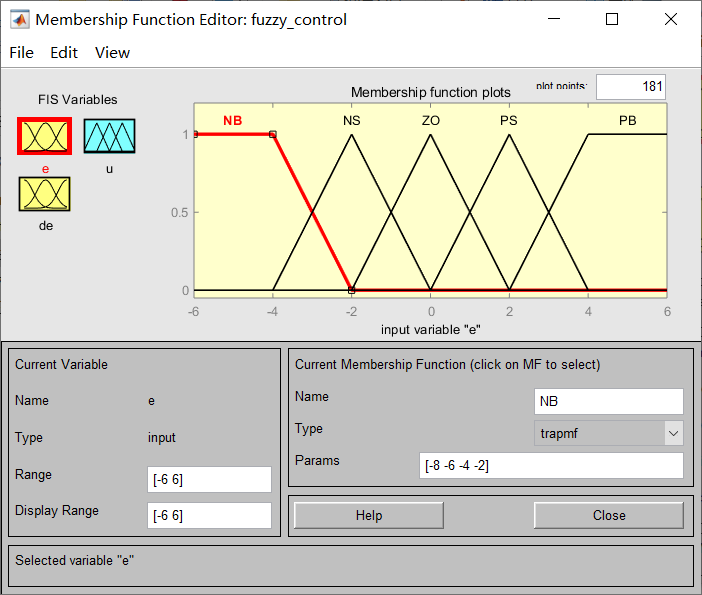
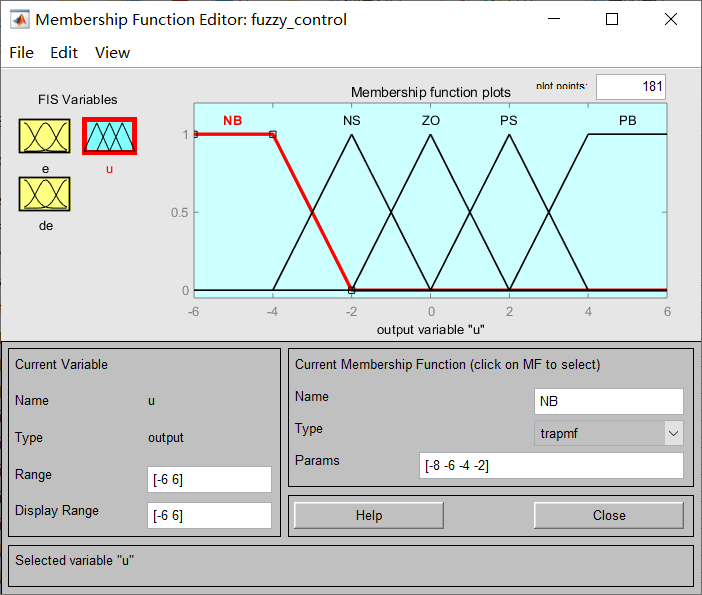
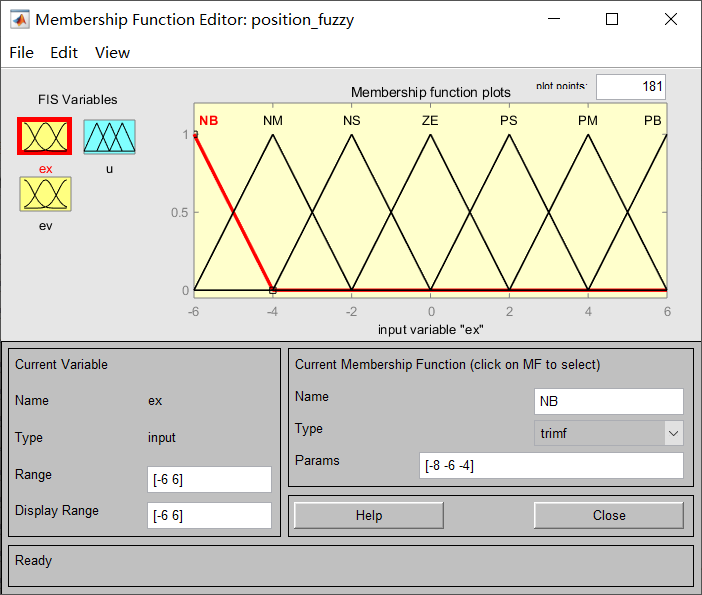
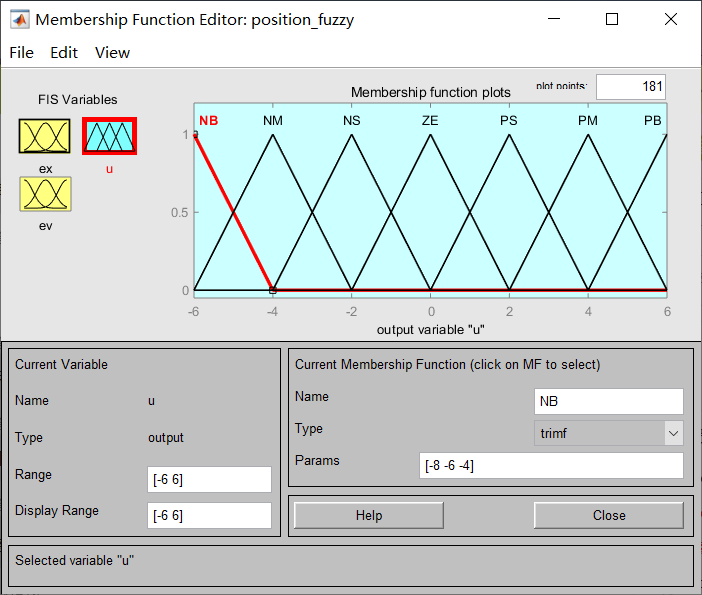
总共有两个输入一个输出，三者模糊集合的划分都相同，此处仅列出误差e和输出u。论域为[-6,6]，模糊集合为5个，分别命名为：[NB NS ZO PS PB]，它们的分布如上图所示。由于在偏差过大时输出的控制应当几乎相同，故两侧的模糊集合曲线为梯形。

模糊规则库的设计：

e\ de	NB	NS	ZO	PS	PB
NB	NB	NB	NB	NS	NB
NS	NB	NB	NS	PB	PS
ZO	NB	NB	ZO	PB	PB
PS	PS	NB	PS	PB	PB
PB	PB	PS	PB	PB	PB

在实际仿真中，经过一系列的实验，我发现在这种参数设置下控制效果最好，但是控制精度似乎还不尽如人意，所以我考虑将位置和角度的模糊控制器分别设计并增加控制器的精度。

改进设计：

模糊集合设计：

总共有两个输入一个输出，三者模糊集合的划分都相同，此处仅列出误差e和输出u。论域为[-6,6]，模糊集合为7个，分别命名为：[NB NM NS ZO PS PM PB]，它们的分布如上图所示。

模糊规则库的设计：

位置规则库：

e\de	NB	NM	NS	ZO	PS	PM	PB
NB	NB	NB	NB	NM	NM	NS	NS
NM	NB	NB	NM	NM	NS	NS	ZO
NS	NM	NM	NS	NS	ZO	PS	PS
ZO	NM	NS	NS	ZO	PS	PS	PM
PS	NS	NS	ZO	PS	PS	PM	PM
PM	ZO	ZO	PS	PS	PM	PM	PB
PB	PS	PS	PM	PM	PB	PB	PB

角度规则库：

e\de	NB	NM	NS	ZO	PS	PM	PB
NB	NB	NB	NB	NB	NM	ZO	ZO
NM	NB	NB	NB	NM	NM	ZO	ZO
NS	NM	NM	NM	NS	ZO	PS	PS
ZO	NM	NM	NS	ZO	PS	PM	PM
PS	NM	NS	ZO	PS	PM	PM	PM
PM	ZO	ZO	PM	PM	PB	PB	PB
PB	ZO	ZO	PM	PM	PB	PB	PB

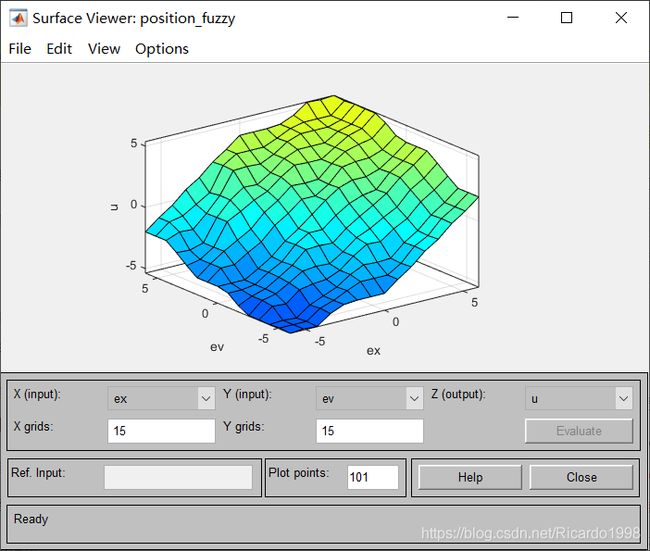
针对位置和角度的不同性质，重新设计模糊控制器，得到的simulink仿真结果得到了显著提高。 在调节参数时，我发现位置误差具有的线性较强，故控制规则曲面接近于平面比较合适；而角度误差的非线性更强，在角度误差和误差微分一个为PB，另一个为NB时，输出控制位ZO最为合适。

三、控制系统仿真程序的设计步骤与运行结果

建立simulink仿真模型：
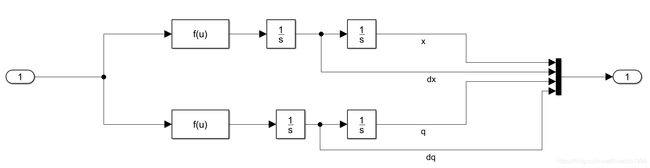
我们将得到的微分方程模型代入simulink中，其中子系统Pendulum Dynamics是倒立摆的模拟，输入量是：$x\dot{x}\theta \dot{\theta }F$ 输出量是下一时刻对应的 $x\dot{x}\theta \dot{\theta }$ 从而实现对系统的仿真。
总体模型：
其中将位置误差、位置误差的微分作为模糊控制器1的输入，将角度误差、角度误差的微分作为模糊控制器2的输入，最后将两种控制效果合成（角度输入控制器效果为正，位置输入控制器效果为负）作为力输入倒立摆子系统中进行计算，子系统将下一步的四个参数反馈回控制器。

子系统：

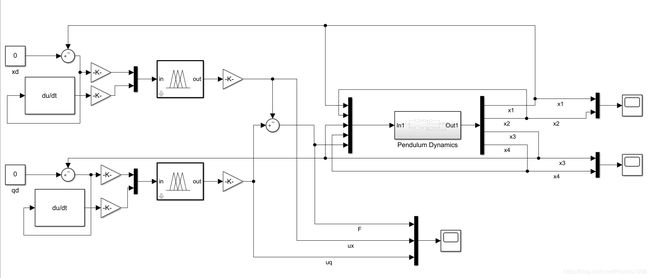
其中的两个函数就分别是上面推导初的和的微分方程表达式。
同时，为了直观观察，我还编写了matlab窗口运行的仿真程序，将模糊控制过程可视化为动画，不过由于整个过程都是用窗口程序单独编写的，在求变量微分时采用的一阶差分来代替，而且为了计算快速仿真时间间隔选用0.01s，窗口仿真动画与simulink仿真曲线稍有差异。其中仿真动画程序参考了GitHub上面的一个项目，地址为：点击访问
运行效果如下图：

原始控制器仿真结果：

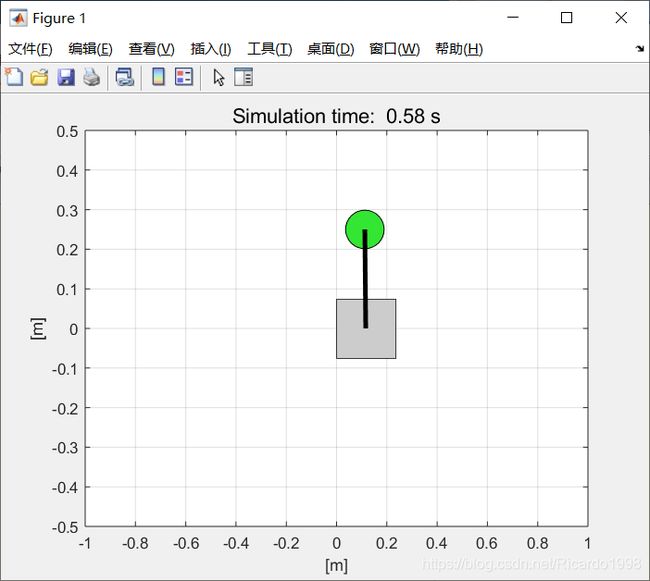
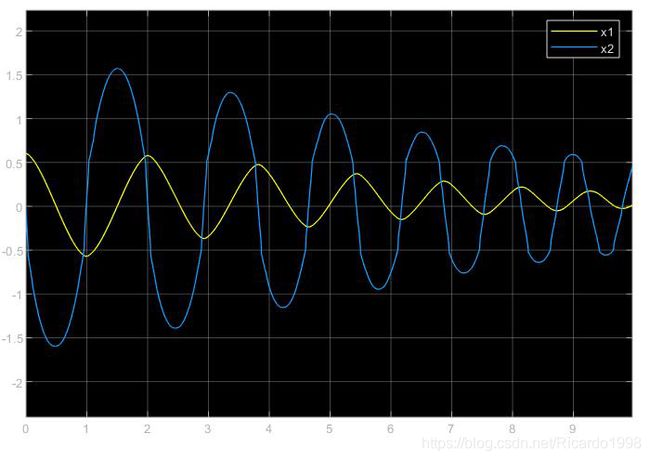
原始控制器位置响应曲线（x1为位置，x2为速度）

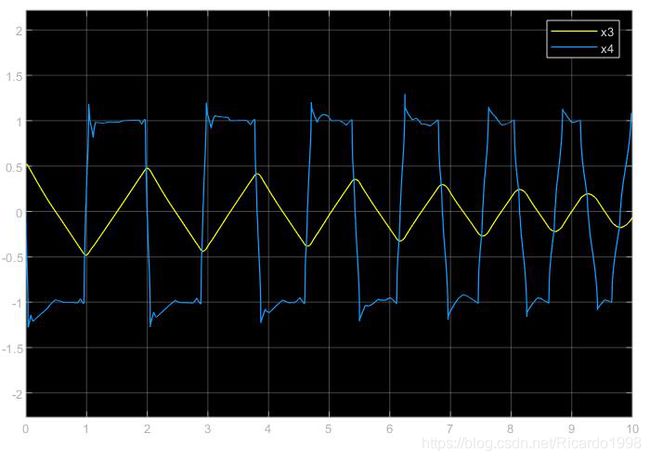
原始控制器角度曲线（x3为角度，x4为角速度）

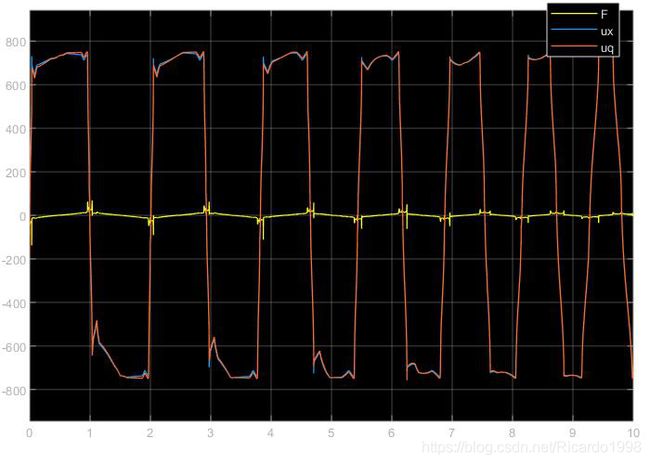
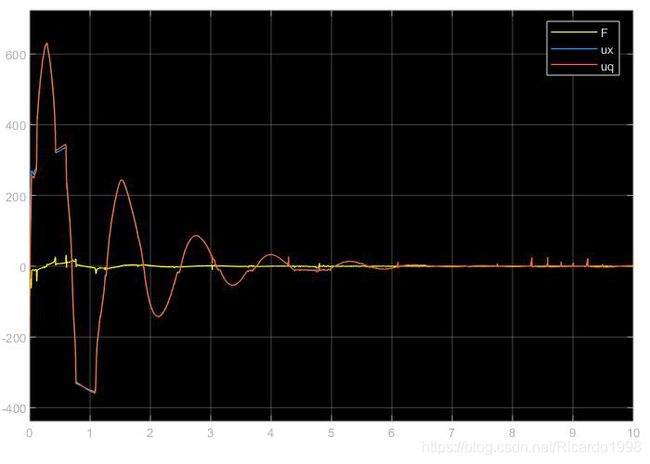
原始控制器输出曲线（F为力，ux为控制器1输出，uq为控制器2 输出）

改进控制器仿真结果：

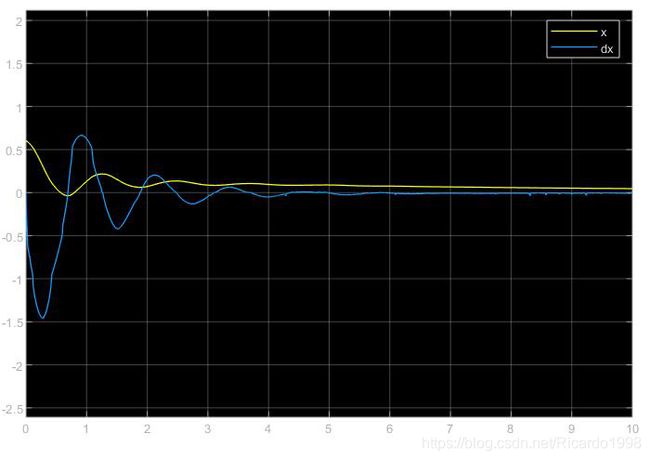
改进控制器位置响应曲线（x为位置，dx为速度）

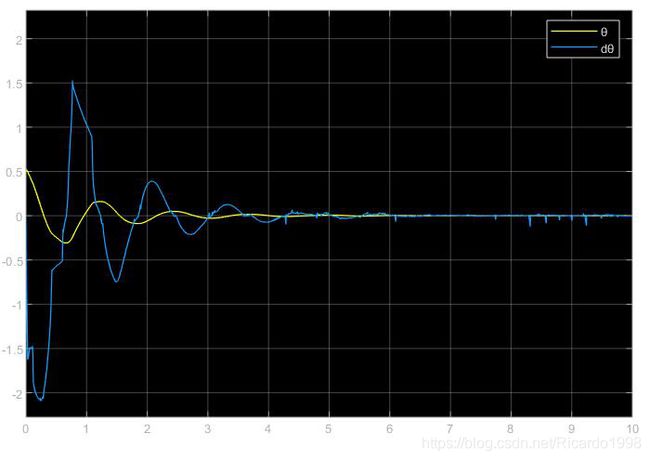
原始控制器角度曲线（θ为角度，dθ为角速度）

原始控制器输出曲线（F为力，ux为控制器1输出，uq为控制器2 输出）

四、总结与结论

从上述仿真结果可以看出，在10秒的仿真时间内，原始模糊控制器虽然可以完成控制，但是控制效果不好，其状态变量会经过较大的震荡，而控制力的输出虽然比较稳定，但合成它的两个模糊控制器输出量也呈现震荡形式。而改进控制器在各种状态参数都稳定的前提下，两个控制器的输出量也呈现收敛的趋势。
但是我在试着用参考资料代入我的模型求解时却遇到了一些问题，相反第一种控制器控制下系统稳定得更快，这可能与窗口程序中时间间隔选取过大等等条件有关。由于这是在不使用模糊控制器设计软件和simulink的前提下编写的程序，比较具有创新性，所以我在提交的作业中还是附上了窗口程序的代码和录制的动画视频。（见“各种图片……”文件夹）
同时，根据simulink求解的结果我也对其进行了动画可视化处理，首先通过运行对应的simulink模型，再运行Animation.m脚本即可查看并录制动画。

备注：后续进行了二级倒立摆的尝试，由于增加的角度变量与前两个状态变量有较强的非线性耦合性，所以模糊规则较难设计。最终只能实现第一级直立，稳定状态下第二级是下垂的，后续在学习相关知识后还会继续努力完成。
源代码下载